I am a theoretical physicist at University of California, Berkeley. Last month, I attended a very interesting conference organized by Foundamental Questions Institute (FQXi) in Puerto Rico, and presented a talk about making predictions in cosmology, especially in the eternally inflating multiverse. I very much enjoyed discussions with people at the conference, where I was invited to post a non-technical account of the issue as well as my own view of it. So here I am.
I find it quite remarkable that some of us in the physics community are thinking with some “confidence” that we live in the multiverse, more specifically one of the many universes in which low-energy physical laws take different forms. (For example, these universes have different elementary particles with different properties, possibly different spacetime dimensions, and so on.) This idea of the multiverse, as we currently think, is not simply a result of random imagination by theorists, but is based on several pieces of observational and theoretical evidence.
Observationally, we have learned more and more that we live in a highly special universe—it seems that the “physical laws” of our universe (summarized in the form of standard models of particle physics and cosmology) takes such a special form that if its structure were varied slightly, then there would be no interesting structure in the universe, let alone intelligent life. It is hard to understand this fact unless there are many universes with varying “physical laws,” and we simply happen to emerge in a universe which allows for intelligent life to develop (which seems to require special conditions). With multiple universes, we can understand the “specialness” of our universe precisely as we understand the “specialness” of our planet Earth (e.g. the ideal distance from the sun), which is only one of the many planets out there.
Perhaps more nontrivial is the fact that our current theory of fundamental physics leads to this picture of the multiverse in a very natural way. Imagine that at some point in the history of the universe, space is exponentially expanding. This expansion—called inflation—occurs when space is filled with a “positive vacuum energy” (which happens quite generally). We knew, already in 80’s, that such inflation is generically eternal. During inflation, various non-inflating regions called bubble universes—of which our own universe could be one—may form, much like bubbles in boiling water. Since ambient space expands exponentially, however, these bubbles do not percolate; rather, the process of creating bubble universes lasts forever in an eternally inflating background. Now, recent progress in string theory suggests that low energy theories describing phyics in these bubble universes (such as the elementary particle content and their properties) may differ bubble by bubble. This is precisely the setup needed to understand the “specialness” of our universe because of the selection effect associated with our own existence, as described above.
A schematic depiction of the eternally inflating multiverse. The horizontal and vertical directions correspond to spatial and time directions, respectively, and various regions with the inverted triangle or argyle shape represent different universes. While regions closer to the upper edge of the diagram look smaller, it is an artifact of the rescaling made to fit the large spacetime into a finite drawing—the fractal structure near the upper edge actually corresponds to an infinite number of large universes.
This particular version of the multiverse—called the eternally inflating multiverse—is very attractive. It is theoretically motivated and has a potential to explain various features seen in our universe. The eternal nature of inflation, however, causes a serious issue of predictivity. Because the process of creating bubble universes occurs infinitely many times, “In an eternally inflating universe, anything that can happen will happen; in fact, it will happen an infinite number of times,” as phrased in an article by Alan Guth. Suppose we want to calculate the relative probability for (any) events 
In the eternally inflating multiverse, however, both 
Over the past decades, some physicists and cosmologists have been thinking about many aspects of this so-called measure problem in eternal inflation. (There are indeed many aspects to the problem, and I’m omitting most of them in my simplified presentation above.) Many of the people who contributed were in the session at the conference, including Aguirre, Albrecht, Bousso, Carroll, Guth, Page, Tegmark, and Vilenkin. My own view, which I think is shared by some others, is that this problem offers a window into deep issues associated with spacetime and gravity. In my 2011 paper I suggested that quantum mechanics plays a crucial role in understanding the multiverse, even at the largest distance scales. (A similar idea was also discussed here around the same time.) In particular, I argued that the eternally inflating multiverse and quantum mechanical many worlds a la Everett are the same concept:
Multiverse = Quantum Many Worlds
in a specific, and literal, sense. In this picture, the global spacetime of general relativity appears only as a derived concept at the cost of overcounting true degrees of freedom; in particular, infinitely large space associated with eternal inflation is a sort of “illusion.” A “true” description of the multiverse must be “intrinsically” probabilistic in a quantum mechanical sense—probabilities in cosmology and quantum measurements have the same origin.
To illustrate the basic idea, let us first consider an (apparently unrelated) system with a black hole. Suppose we drop some book
A puzzling thing occurs, however, if we observe the same phenomenon from the viewpoint of an observer who is falling into the black hole with a book. In this case, the equivalence principle says that the book does not feel gravity (except for the tidal force which is tiny for a large black hole), so it simply passes through the black hole horizon without any disruption. (Recently, this picture was challenged by the so-called firewall argument—the book might hit a collection of higher energy quanta called a firewall, rather than freely fall. Even if so, it does not affect our basic argument below.) This implies that all the information about the book (in fact, the book itself) will be inside the horizon at late times. On the other hand, we have just argued that from a distant observer’s point of view, the information will be outside—first on the horizon and then in Hawking radiation. Which is correct?
One might think that the information is simply duplicated: one copy inside and the other outside. This, however, cannot be the case. Quantum mechanics prohibits faithful copying of full quantum information, the so-called no-cloning theorem. Therefore, it seems that the two pictures by the two observers cannot both be correct.
The proposed solution to this puzzle is interesting—both pictures are correct, but not at the same time. The point is that one cannot be both a distant observer and a falling observer at the same time. If you are a distant observer, the information will be outside, and the interior spacetime must be viewed as non-existent since you can never access it even in principle (because of the existence of the horizon). On the other hand, if you are a falling observer, then you have the interior spacetime in which the information (the book itself) will fall, but this happens only at the cost of losing a part of spacetime in which Hawking radiation lies, which you can never access since you yourself are falling into the black hole. There is no inconsistency in either of these two pictures; only if you artificially “patch” the two pictures, which you cannot physically do, does the apparent inconsistency of information duplication occurs. This somewhat surprising aspect of a system with gravity is called black hole complementarity, pioneered by ‘t Hooft, Susskind, and their collaborators.
What does this discussion of black holes have to do with cosmology, and, in particular the eternally inflating multiverse? In cosmology our space is surrounded by a cosmological horizon. (For example, imagine that space is expanding exponentially; this makes it impossible for us to obtain any signal from regions farther than some distance because objects in these regions recede faster than speed of light. The definition of appropriate horizons in general cases is more subtle, but can be made.) The situation, therefore, is the “inside out” version of the black hole case viewed from a distant observer. As in the case of the black hole, quantum mechanics requires that spacetime on the other side of the horizon—in this case the exterior to the cosmological horizon—must be viewed as non-existent. (In the paper I made this claim based on some simple supportive calculations.) In a more technical term, a quantum state describing the system represents only the region within the horizon—there is no infinite space in any single, consistent description of the system!
If a quantum state represents only space within the horizon, then where is the multiverse, which we thought exists in an eternally inflating space further away from our own horizon? The answer is—probability! The process of creating bubble universes is a probabilistic process in the quantum mechanical sense—it occurs through quantum mechanical tunneling. This implies that, starting from some initially inflating space, we could end up with different universes probabilistically. All different universes—including our own—live in probability space. In a more technical term, a state representing eternally inflating space evolves into a superposition of terms—or branches—representing different universes, but with each of them representing only the region within its own horizon. Note that there is no concept of infinitely large space here, which led to the ill-definedness of probability. The picture of initially large multiverse, naively suggested by general relativity, appears only after “patching” pictures based on different branches together; but this vastly overcounts true degrees of freedom as was the case if we include both the interior spacetime and Hawking radiation in our description of a black hole.
The description of the multiverse presented here provides complete unification of the eternally inflating multiverse and the many worlds interpretation in quantum mechanics. Suppose the multiverse starts from some initial state 
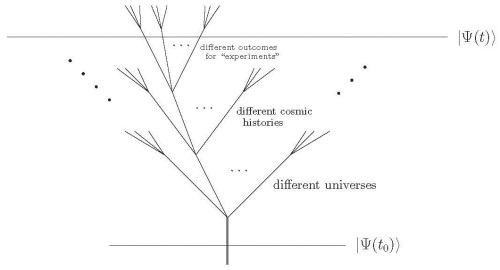
A schematic picture for the evolution of the multiverse state. As t increases, the state evolves into a superposition of states in which various bubble universes nucleate in various locations. Each of these states then evolves further into a superposition of states representing various possible cosmic histories, including different outcomes of experiments performed within that universe.
The picture presented here does not solve all the problems in eternally inflating cosmology. What is the actual quantum state of the multiverse? What is its “initial conditions”? What is time? How does it emerge? The picture, however, does provide a framework to address these further, deep questions, and I have recently made some progress: the basic idea is that the state of the multiverse (which may be selected uniquely by the normalizability condition) never changes, and yet time appears as an emergent concept locally in branches as physical correlations among objects (along the lines of an old idea by DeWitt). Given the length already, I will not elaborate on this new development here. If you are interested, you might want to read my paper.
It is fascinating that physicists can talk about big and deep questions like the ones discussed here based on concrete theoretical progress. Nobody really knows where these explorations will finally lead us to. It seems, however, clear that we live in an exciting era in which our scientific explorations reach beyond what we thought to be the entire physical world, our universe.
Quantum Frontiers 
Is there some sort of symmetry in your multiverse?
are there so called entangled anti- copy bubble universes possible?
see perhaps:
Democratic Free will in the instant entangled copy multiverse.
Click to access 1401.0071v2.pdf
Pingback: The Multiverse, Evidence and Theology | Not Even Wrong
Yasunori, you linked to the Bousso/Susskind paper, but didn’t to the earlier Tegmark/Aguirre paper (http://arxiv.org/abs/1008.1066). Are these ideas distinct?
Yes, these ideas are distinct. They do not take the view of spacetime which led us to take the view as described, i.e. the multiverse lives (only) in probability space.
Fascinating…So, in your view, Tegmarks Levels I&II are redundant, only level III is required? What is your stand-point on Max Tegmarks further hypothesis that the Multiverse is part of a mathematicl structure and potentially falsifiable in future experiments?
…further, in your theory, does it mean that the Probability Space from my viewpoint as an observer, includes any probability I could perceive also outside the event horizon of that viewpoint? I e, That any event with non-zero probability, say e g inside the massive black hole at the center of our Milky Way Galaxy, also has non-zero probability from my current viewpoint? I am most grateful for your reply. Sorry if I layman misunderstand everything :-).
Fascinating line of thinking. Consider the following: Every universe is as special as each other, like earth has a special condition to be earth. This is true for each and every situation and so thing. This is general uniqueness. Special uniqueness is derived by observation. With it an observer observes a unique situation by excluding all others. This makes the observation of this universe and no other.
Time can be seen as the step by step acknowledgement of all movements of a universe. All the movements of a universe form together the time span of that universe. That time span can be called the total event of that universe. That total event is one of all possible events that universe could have been by all the movements it could have had made. All its possible events are made in what is to call Hyparxis.
The same is true for any other universe. The hyparxis of all universes is in Eternity. Eternity is not in that respect eternal or infinite time, but the total of all possibilities with each and every universe, however infinite the whole of all universe will be (see Georg Cantor and set theory).
Because every universe has its hyparxis, so does every “being” have its hyparxis. Because of that each being is an eternal being. The prerequisite to be really eternal is to acknowledge, to know, to experience, to be aware of, to be consciously to learn to be that being.
I don’t think we have any choice in the matter. We are that being. Are “we” evolving or are we playing a game? We seem to exist……….is that but an illusion, or a “real” creation of some sort? Is my personal “I” just a probability?
That is, like the cat in the box, is my reality undetermined until observed?
Am I my own observer? I trust you youngsters with the math……the philosophical implications make me dizzy.
Thank you for such an interesting post, which will need at least another read I think.
But I’m curious about the ‘specialness’ of our universe. In what sense are we supposed the think the universe is special? Surely not the apparent fine tuning. For example, it it were the case that all universes necessarily had to behave as our does (as represented by our models, the laws of the universe), then ours wouldn’t be special. Surely it’s not the ‘fine tuning’ of our laws that are special in themselves or that make our universe special, if they are necessarily what they are, because of the way universes emerge (from whatever they emerge from).
I can only imagine it being worth the label ‘special’ if we knew enough to say that universes that are ‘tuned’ as ours is are very unlikely. Do we know that ours is actually special? Do we know enough to say that the tuning, as fine as it appears, is uncommon in the business of universes?
If some philosopher or any other non-physicists asked why is our universe special, shouldn’t the answer not not be “We don’t know why, yet, but a multiverse might explain that”, but rather “We don’t know that it is special.”
We think our universe is special in that it has highly non-generic properties in space of possible theories. A good example is the value of vacuum energy. In order to have any interesting macroscopic structure, it must take a value tuned at the level of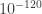
or so. All the other values lead to universes without any structure. Our universe lies precisely in the (tiny) region in which interesting large scale structures occur. (As an analogy, you might imagine a curve 
, and think our universe lies at 
with other universes corresponding to all possible values of 
. The region 
is clearly special in that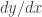 
is significant only there.) A similar feature is also known for the value of the weak scale: if it were more than a factor of a few larger, then there would be no atom other than hydrogen. (You might be interested in http://arxiv.org/abs/arXiv:0712.2454 in which I studied the issue related to your question.)
Experimental tests? Any predictions that can be tested with present data?
At the moment, the most significant observational “evidence” for the multiverse is the value of vacuum energy. It was historically a big mystery why the vacuum energy in our universe is some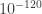
orders of magnitude smaller than the naive expectation from theory. There were significant efforts explaining this smallness theoretically over decades without much success. The hope was that there is some unknown mechanism making the vacuum energy zero, although people couldn’t find even that. Already in 80’s, however, Weinberg (and others) thought that if there is a multiverse, i.e. many universes in which vacuum energy varies, then the smallness can be explained through anthropic selection (although he did not use the word “multiverse”). A prediction of this scenario was that vacuum energy will not be (much) smaller than that needed for the existence of life, i.e. it will be (roughly) comparable to the energy density of matter. This is exactly what was found in 1998 by the discovery of accelerating expansion of the universe (Nobel prize 2011), which in its simplest interpretation implies the existence of vacuum energy within about a factor 2 of the matter energy density.
Similar signatures, which are (extremely) hard to understand in the conventional thinking but can naturally happen in the multiverse, may be found in the future. For example, the multiverse can naturally lead to a small nonzero negative curvature in our universe (first pointed out in http://arxiv.org/abs/hep-th/0505232). It would be difficult to understand such a result in conventional cosmology (without unexplained fine-tuning). Interestingly, a discovery of a wrong sign, i.e. positive, curvature would falsify the multiverse as we think now, and exploration of curvature might also give us information about possible measures in the multiverse (see e.g. http://arxiv.org/abs/arXiv:1203.6876).
You might think it unsatisfactory that evidence we imagine gathering here is, in some sense, indirect. This is, however, not much different from some other situations—e.g. in the big-bang theory, inflationary cosmology, and Darwinism in biology— at the conceptual level (although the significance of the evidence we currently have is different). We have not directly “seen” any of these phenomena—we simply postulate a theory and test if what we observe are consistent with it. If we accumulate evidence that can be naturally explained by that theory, but not in other way, then we gradually accept it as a provisional theory of the world we live. In this sense, the multiverse is the best theory we currently have to explain the smallness of the vacuum energy. If we are lucky, we might see more “direct” evidence such as a signal from a collision of bubble universes (see e.g. http://arxiv.org/abs/arXiv:1107.2593), but even that would not “prove” the existence of the multiverse, and we must keep seeking phenomena that can naturally occur in the multiverse but not in other ways. It is true that any demonstration along these lines would not be as dramatic as, e.g., a discovery of a new particle, but here we are asking really a big question, and this is the cost for it. At least, theoretical explorations of such new phenomena/scenarios (reasonable only in the multiverse context) would stimulate new experimental explorations. Hopefully, we will find one or more of them in the future.
Thank you for your thoughtful reply. I’m an old fashion experimentist and I guess I’m looking for a graph of some sort of experimental data with a theory curve on the graph similar to the data. I also have the same feeling for string/m-theory.
Your comments on curvature are new to me.
Again thank you
“This is, however, not much different from some other situations—e.g. in …Darwinism in biology”
It’s very different from that.
http://en.wikipedia.org/wiki/Experimental_evolution
My question might seem naive because I am not at all a specialist in cosmology, but here it is:
if someone else is a few kilometers away from me outside my past or future light-cone, doesn’t she have, strictly speaking, a slightly different horizon? Then how is it that the bubble-universe we are in have a definite boundary (or alternatively, that different superposed states be clearly separated independently from one’s perspective)?
“It is hard to understand this fact unless there are many universes with varying “physical laws,” and we simply happen to emerge in a universe which allows for intelligent life to develop (which seems to require special conditions).”
I am very troubled by this line of reasoning. Does everything unique or complicated require an infinite multiplicity to explain its existence? Parity of reason would seem to demand this be the case, but that line of thinking is obviously absurd. We don’t require an infinite number of dogs to explain why this dog has this kind of tail and those kinds of ears. So why do we require an infinite number of universes to ‘explain’ why this one has these laws and not others? Moreover, biologists would be aghast is your response to “Why does this dog have these ears and that tail?” was “There are lots of dogs and this is one of them so we’re just lucky to be looking at the dog that has those features.” That isn’t any kind of explanation at all. It lets the biologist off the hook for the entire evolution of dogs, they no longer have to explain anything about how dogs got to as they are at all.
This unhinges science from explanation. Everything is answered by pointing at the multiplicity and claiming that what is to be explained is just some incidental fact about the multiverse as a whole. Answers to real questions start to sound like zen koans “There are many and we are one, that’s just the way it is.” That’s not good science.
I totally agree with this comment. The anthropic argument seems to result in a conflation of physics and metaphysics. Metaphysics is not a pejorative term for me (I view it as the analysis of conceptual possibilities, which can well be informed by science and empirical data) but metaphysics is not physics, it concerns, among other things, the (possible) interpretation(s) of physics.
The line of reasonning presented in this article seems to eschew some conceptual issues by allowing, loosely speaking, all physical possibilities to barely exist… Which makes physics look a lot like metaphysics. But doesn’t it amount to recognize our failure to provide a physical explanation for the observed phenomenon?
For this reason I am not at all convinced that indirect evidence (provided in another comment by the author) is evidence in the same sense as evidence for the big bang, as far as it amounts to say: there can be no standard explanation, so multiverse. But did we *prove* in anyway that there cannot be any other unimagined explanation?
I don’t think this is a legitimate move. In any case it is clearly a metaphysical move.
Another point which might be related is how we are willing to interpret the notion of probability.
This notion often comes unanalysed in scientific litterature, which is a notorious difficulty for the many-world interpretation and the derivation of the Born rule (Deustch-Wallace theory is an interesting attempt to overcome it but I think it does not definitely settle the issue). If every outcome exists, are we still talking about probabilities?
An observation which may not lead anywhere: in the branching diagram, since the cardinality of the levels of vertical axis is countably infinite, the cardinality of the points on the horizontal axis is uncountably infinite. Would there be a model of the Reals in the physical universe? Are the branches at each branch point finite and ordered? Would there be a model satisfying the Axiom of Choice?
Hm. Well, one should never reply to oneself, but: the vertical axis is countably infinite if there’s a clock that ticks and says, Now branch. Otherwise, maybe we’re uncountable all the way down. (It was nice to have turtles.)
Not being a physicist, I struggle with these concepts, but still the idea of a multi-verse seems to me like a bad interpretation of mathematical equations. I have a different take.
What we know is that quantum systems in superposition collapse into one and only one outcome. We also know that observation makes the superposition collapse (although there may be other reasons – I’ve recently read that size considerations may limit this quantum behavior). As this article points out, we have also observed that our universe is highly special. The chance that our laws of physics being what they are is virtually impossible, unless is one of an infinite number of universes. I believe in a different explanation. What if in its inception our universe was in a quantum state such that infinite possible laws of physics were in superposition. Then why did our universe collapse into our special outcome? Well, because we would be here to observe it!
We can actually test this mechanism using the following experiment. Let’s consider a complex system in quantum superposition with multiple degrees of freedom hidden from observation, in all but one case. Upon collapse, only in 1 of N possible outcomes, a chain of events is triggered that will reveals this event to an observer at a later time. If such experiment consistently favors the one special outcome, it may be hint that there is no need for a multi-verse.
This is precisely what happens in a quantum experiment, except that the one special outcome corresponds to a superposition of outcomes for the degrees of freedom which are not measured.
The problem is that you need to measure a degree of freedom if you want to know whether it is “favoured” or not but if you do it is “favoured”…
Different interpretations of quantum mechanics (collapse, bohmian or many world) are undermined by experiment: no experience can decide which is the good one.
Good paper! Can’t follow the math but I THINK I follow the English. Thank you!
“[The Multiverse] is based on several pieces of observational and theoretical evidence. Observationally, we have learned more and more that we live in a highly special universe.”
Rather in line with ‘Quentin’ above, I don’t find that this comment provides any evidence whatsoever for the existence of the multiverse. It’s simply an observation which encourages some, with a certain worldview, to speculate about the existence of the multiverse. It adds no evidential support to that metaphysical viewpoint.
Hi Dr. Nomura, would you mind commenting on your static quantum multiverse paper http://arxiv.org/abs/arXiv:1205.5550 about how exactly time can emerge from a static |psi>? While it follows from the 2 hypotheses that H|\psi>=0, I can’t quite identify an operational way to reconstruct the perceived “time parameter” from the multiverse wave function. Before in the t-dependent case we can still somehow attach a quasi-physical meaning to t and convinces myself that the history of multiverse can be identified by tracing through some selected branch of the wavefunction, but now it seems to me that the only way to recover “time” is by “jumping between different branches of the static |psi>” using the extended Born Rule introduced in the paper and ask questions with respect to certain physical configurations…is that roughly the idea? Also, I am quite confused by section 5.3, what does it mean to have processes in eq(8) for generic |psi(t)> balanced by inverse processes in |psi>?
Nice read! I do remember reading in ancient Indian text mentioned that there are universes upon universes. We recently published an article which attempts to satisfy the curiosity that if we are living in a multiverse then how far can be our closest neighbors?
http://www.blueplanetjournal.com/cosmos/mapping-the-multiverse-how-far-to-the-next-universe.html
Pingback: The theory of everything: Help wanted | Quantum Frontiers
Multiverse Contact
Contact to Parallel Universe / Multiverse via Subspace.
Knowing The Fourth Dimension,The Fifth Dimension,The Sixth Dimension and The Seventh Dimension.
Is this a Philosophical Post or a Scientific Post? I mean on which observation and or facts, unlike the ones Science already has, are you basing this on? It is like the story of a human being raised alone inside a self sustained cube his whole life. Sooner or later he thinks there are many other cubes like his just outside his wall, when in reality the World is much different than that. We can’t barely see the Universe’s Edge, let alone touch it….You have made a construct based on Faith or Believe, and Science is not based on Faith, it is based on observations, data, theories, numbers, mathematical equations, etc…Your construct around this theory calls this Universe, our Universe, “Special”….If it is so,then why don’t you call out the probability that we are in a Special Universe in the Multiverse? Math is the Reason by which Science is proven. And please don’t tell me that there are “infinite” numbers of universes, since in a finite, time-limited universe like ours there would never be enough time to prove this.
BTW I am still waiting for the LHC to prove Brian Greene’s thoughtfully articulated M-Theory….I am still hearing the crickets.
The multiverse is not falsifiable so in a Popper sense it is not science. One chance of possibly observing another outside universe is a collision with ours in our early history as the author mentioned. It is unclear if that is a unique signature. Such an event has not been observed. IMHO the discussion of the multiverse is metaphysics. You might want to read the blog Not Even Wrong to get a better discussion on the problems with the multiverse
If your an Atheist who entered cosmology to combat the big bangs implications of design…you might say its hard to explain the fine tuning. You might even say its hard to explain why snow is white if your blind but it’s really not that hard to someone who isn’t heavily biased toward atheism. The implications are obvious. Just as the BB was. Just as DNA Code was.
There is so much bias now they want to lower the threshold of science. So in all of history the first time they want to change the rules of science is when the data point to a Creator. When you want to flee from the standards of science and run to a hypothesis(its not a theory) that actually undermines all of science, things are desperate. This is gonna make Einsteins “blunder” look like childs play. This current crop of scientists are gonna go down as so pathologically biased that no one will ever trust them again.
Pingback: Multiversal Journeys | Not Even Wrong
IMHO I would suggest that we iive inside one of an even set of (anti)-copy universes as the origin of our consciousness and the one particle interference double slit effect.
see:
https://www.academia.edu/6781821/The_Navel_Cord_Multiverse_with_Raspberry_Shape_a_Super_Symmetric_Entangled_12_Fold_Bubble_Universe
Info sangat menarik, sukses ya mas.. , Adrianne
From everything i have been able to learn on this subject so far it appears: Every decision that all of our individual ancestors have made, ad infinitum, combined with the cumulative effect of every choice, thought, decision, and action, whether conscious or unconscious, has systematically carved out the “multiverse” or Universe, which we, you, or I, are currently experiencing from our perspective as observer of SpaceTime. That is, the world we inhabit, is the world we have created through our own choices of Free Will, and other Unconscious and Conscious behavior, thoughts, actions, and choices. This is a multi-player game however, and others are all doing the same thing. There seems to be a connection or direct pathway between multiverses, where the realities of other multiverses are affecting the multiverse which we inhabit. i.e. Other Persons. However if are viewing the world through your eyes, you are inhabiting your own Universe, which ‘you’ have created through your choices, and has been affected by the infinite choices of an infinite amount of other persons. The conscious observer creates the perception of TimeSpace through observation, and the entire Universe which you perceive is fundamentally a creation of the experience of your consciousness. The Universe is relative to the observer. i.e. SpaceTime. So whatever you are seeing or experiencing in the world, is the result of your self, combined with the other selfs of the Multiverse, although the fundamental bedrock of the experience derives from our conscious observation of the Quantum Bubble Soup, relative to what path you chose to arrive at the present moment of Nowness. With your own individual death experience sometime in the future, will come the ‘End of Time’, relative to the observer. Thus from your, or mine perspective, with the cessation of consciousness will come the end of TimeSpace, and thus the end of that particular multiverse which we have created for ourselves. I cannot experience the world looking through your eyes, and vice versa, thus we each inhabit our own particular universe which is a byproduct of all of all other multiverses, combined with the one we have carved out of the Multiverse to be our own inhabited Universe which we experience as ‘Reality’. The radical implications of this are basically that we radically and literally create our own reality, and that the whole world is all in your head. It is possible to self-experiment with the multiverse. Simply explore the possibilities of different choices you make with your own Free Will. You get to choose what you eat for breakfast, French Toast, or Oatmeal ? You get to choose who you make your wife or husband. You get to choose what you choose to study or not study. Your choice what kind of job you aspire to, or have. Your choice what State, City, or Country you live in, and when, and for how long. ad infinitum. You will quickly see that the whole world you experience, is the world which you do. Instant Karma. You can’t control other people of course, as they are Master’s of their own Universe. The Multiverse is really like a Universe, it’s all One. We are all Master’s of the Universe, if only we recognized the nearly incomprehensible power of our own Free Will. We my fellow sentient beings, are the creators and destroyers of worlds. Only God knows what lies beyond the boundaries of the event Horizon, and has a birds eyes view of all Multiverses simultaneously, Eternally, outside of SpaceTime. We will return to our origin with the Creator of all creation, at the end of TimeSpace, but until then, carry on, create your own Universe with the utmost care, and love, and kindness for others, and accept the awesome power of Free Will in every nanosecond of existence. You my friend are the creator of what you experience as Time and Space, through your consciousness, which perhaps was made in the image of the absolute consciousness of God. Consciousness is the absolute foundation and bedrock of the Universe, out of which all physical phenomena arise. Choose wisely, and do Good. Let me know if i am missing something here. I am not up to date on the maths, but well read and o.k. at rational thinking and logic. Sun and Rain Works: It’s the stuff life is made out of, Literally.
Wonderful comment Joe. I have only one little objection.
You say at the end: “Consciousness is the absolute foundation and bedrock of the Universe, out of which all physical phenomena arise”.
To my understand that is not true. It is: “Love is the absolute foundation and bedrock of the Universe, out of which all physical and non-physical phenomena arise”.
Consciousness is the first phenomenon originating from it and so the all-accompanying means to be aware of what Love made and makes possible.
Without Love as mother, consciousness never could be such a wonderful “thing”.
You have blown my mind, I just love it… thank you very much. I wish I had another 70 odd years to think about this.
I see things you cannot. We are made of stars and black holes; I am you, you are me, we are the same but different .
I have things to say but can only think them…
Pingback: Some Other Scientific Theories the GOP Should Debate – Trending News
Pingback: Some Other Scientific Theories the GOP Should Debate – Newz Corner
Pingback: Some Other Scientific Theories the GOP Should Debate – Grouvy Today
Pingback: Some Other Scientific Theories the GOP Should Debate - LI Tech News
Pingback: Some Other Scientific Theories the GOP Should Debate – Global News
Pingback: Some Other Scientific Theories the GOP Should Debate – Credence Nation
Pingback: Some Other Scientific Theories the GOP Should Debate
Pingback: Some Other Scientific Theories the GOP Should Debate | News
Pingback: Some Other Scientific Theories the GOP Should Debate