The RSS subscriptions which populate my Google Reader mainly fall into two categories: scientific and other. Sometimes patterns emerge when superimposing these disparate fields onto the same photo-detection plate (my brain.) Today, it became abundantly clear that it’s been a tough week for hidden variable theories.
Let me explain. Hidden variable theories were proposed by physicists in an attempt to explain the ‘indeterminism’ which seems to arise in quantum mechanics, and especially in the double-slit experiment. This probably means nothing to many of you, so let me explain further: the hidden variables in Tuesday’s election weren’t enough to trump Nate Silver’s incredibly accurate predictions based upon statistics and data (hidden variables in Tuesday’s election include: “momentum,” “the opinions of undecided voters,” and “pundit’s hunches.”) This isn’t to say that there weren’t hidden variables at play — clearly the statistical models used weren’t fully complete and will someday be improved upon — but hidden variables alone weren’t the dominant influence. Indeed, Barack Obama was re-elected for a second term. However, happy as I was to see statistics trump hunches, the point of this post is not to wax political, but rather to describe the recent failure of hidden variable theories in an arena more appropriate for this blog: quantum experiments.
The November 2nd issue of Science had two independent papers describing the results of recent delayed-choice experiments. The goal of these papers was to rule out hidden variable theories as an explanation for aspects of quantum mechanics. More specifically, the experiments showed that the wave-particle duality which results during measurement in the double-slit experiment cannot be explained by combining classical mechanics with local hidden variables. This won’t come as a surprise to people who deal with quantum mechanics on a daily basis (consciously), but it’s nice to have additional material to refer to quantum naysayers, and the experimental set-ups were impressive.
Before describing these two experiments, I want to introduce John Wheeler’s delayed choice thought experiment. As a primer, one should first be familiar with the double-slit experiment, but read along anyways even if you’re unacquainted, because there are interesting ideas accessible at all levels. Also, maybe it will motivate you to ponder the double-slit experiment, which Feynman is often quoted as saying ‘contains the only mystery of quantum mechanics’ (measurement is weird.)
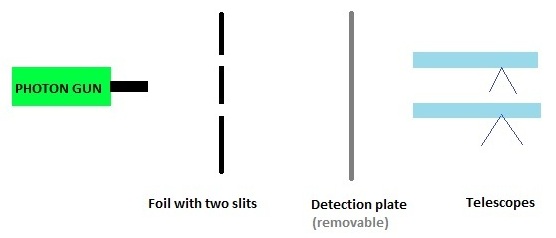
The tragic life of a photon: from creation to annihilation in nanoseconds, and misunderstood along the way. This image shows the experimental setup for the delayed choice double-slit experiment. The set-up differs from that of the usual double-slit experiment because the detection plate is removable. When it is in place, the wave-like nature of photons is probed. When it has been removed, the photons travel to two telescopes and will be measured to arrive in only one of them, thereby probing the particle like nature. If the distance between foil and plate is large enough, then the experimenter can decide whether to keep or remove the plate once the photons have already passed beyond the foil, thereby ruling out hidden variable theories (other than those which can perturb the photon in free space.)
As a brief review, one version of the dual slit experiment proceeds as follows:
- A ‘photon gun’ fires a single photon towards a detector.
- Before reaching the detector, the photon passes through a sheet of aluminum foil which has two slits cut into it (imagine two medieval arrow-slits, but smaller.)
- After passing through the foil with the slits, the photon travels through free space for a while and then arrives at a photo-detection plate (this is similar to photographic paper, which is originally black and records a white dot every time a photon hits a point on the paper.)
- The weirdness happens in between steps 2 and 3. If any attempt is made to observe the photon after it has passed beyond the foil with the slits, or if one of the slits itself is observed, then the photon behaves as a particle. If no observations are made until after the photon hits the photo-detection plate, then the photon behaves as a wave. These different behaviors are confirmed by sending many photons through the device, but only one at a time. If you’re unfamiliar with this experiment, you should think through what would happen if you sent a water wave versus shooting infinitesimal pellets through the slits.
That’s probably mind-numbingly boring review for most of you, but you might not be familiar with Wheeler’s delayed-choice twist. There used to be a school of physicists which advocated that the dual slit experiment could be explained in terms of local hidden variables. Imagine there were hidden variables at the double slit, so that as the photon passes through the slits, the hidden variables “tell it” whether its wave-like or particle-like nature will be measured. The act of passing through the slits could then change the state of the photon into the appropriate paradigm: wave or particle. Wheeler proposed the following thought experiment:
- Change the experimental setup slightly by moving the photodetector plate far away from the double slit — far enough that the experimenter will be able to manipulate the plate in the time interval between when the photon passes through the slits and arrives at the plate. Also, position two telescopes behind the plate, with one telescope pointed at each of the two slits.
- Now for the delayed-choice part. After the photon has passed through the slits, the experimenter flips a coin, and depending on the outcome, either keeps the photodetector in place and probes the wave-like nature of the photon; or removes the photodetector so that the photon travels towards the telescopes and then is measured as only going through one of them — thereby probing the particle-like nature of the photon.
If the act of flipping the coin and then moving the photodetector was “space-like separated” from when the photon passed through the slits, and wave-particle duality was still observed, then local hidden variables alone could not explain the experimental outcome (at least hidden variable theories which could only influence the photon when it interacted with some non-trivial part of the system.) Versions of this experiment had previously been carried out which decisively demonstrated the wave-particle duality that we’ve come to expect from photons. However, the two recent Science papers in question used quantum-information variants of this delayed-choice experiment to hammer additional nails in the coffin of local hidden variable theories.
In the first paper, “A Quantum Delayed-Choice Experiment,” a team from the University of Bristol used tools from quantum information to perform a variant of the delayed-choice experiment. More specifically, they send polarized photons through a Hadamard gate which splits each photon into two polarization modes, they then apply a relative phase shift to one of the modes, followed by a controlled Hadamard gate which recombines these modes. Using some fancy footwork they are able to carry out a delayed-choice experiment where instead of carrying out step 2 above (flipping a coin and then moving the detector, in a space-like separated manner,) they test a Bell inequality and obtain non-local correlations which violate said inequality. This has equivalent ramifications as step 2 above and as what Wheeler originally proposed.
In the second paper, “Entanglement Enabled Delayed-Choice Experiment,” a French team used entanglement as their surrogate for space-like separation. More specifically, they use a pair of polarization entangled photons, where one is the test photon, and the other is the “corroborative” photon. Even after detection of the test photon, depending upon how they measure the “corroborative” photon, they can toggle whether they probe the wave-like or particle-like nature of the test photon. They can do this even after detecting the test photon, as long as no one has looked at the results (they can know that the photon arrived at the photo-detection plate, but they can’t look at the white dot yet.) Quantum mechanics truly is weird. Along these lines, a Caltech professor once made an off-handed comment which stuck with me: “the greatest opportunities are in the extremes.”
In conclusion, not all of the undecided American voters showed up at the polls on Tuesday and suddenly decided to vote for Mitt Romney — as some of the “momentum” espousing pundits expected. These election based hidden variables proved to be inconsequential. Hidden variable theories also had a tough week in physics. My personal take-away is this: I’m going to be an obedient grad student by trusting the data and shutting-up and calculating… at least for the next few days.

Here is another new paper this week claiming results against hidden variables.
http://arxiv.org/abs/1211.0942
Thanks very much for the reference.
Good lord, this is not really so complicated. The most famous and well-developed “hidden variables” theory, due to de Broglie and Bohm, would perfectly predict the outcomes of these experiments. If you want to say that these are further experimental proofs against LOCAL theories, fine. The de Broglie/Bohm theory, like the GRW collapse theory (and, for that matter, the “standard view” if there is such a thing) are all non-local, as Bell showed they must be. But that has nothing at all to do with “hidden variables”.
Tim, you’re absolutely right that these experiments only rule out LOCAL hidden variable theories — and more specifically, ones where the hidden variables “act” at the location of the sheet with two slits. However, I don’t feel like it’s giving too much by not explicitly using the word ‘local.’ The wavefunction itself can be interpreted as a nonlocal hidden variable theory.
Regarding how “complicated” these experiments were, I agree that the set-ups weren’t particularly intricate and that the final result isn’t too difficult to comprehend, but I don’t think it’s fair to say “this is not really so complicated.” These experiments are deep: the second experiment shows that even after photons have been detected and thereby ‘destroyed,’ the wavefunction still hasn’t collapsed, as can be evidenced by toggling the system paramaters of their interferometer, and steering the already detected photon to behave either as a particle or as a wave.
Thanks for your comment, it forced me to think through these experiments again.
It’s not true. Both local realist theories as well as all ever proposed nonlocal realist theories have been excluded – and they’ve been really known to be wrong from the 1920s, too. For a very specific refutation of a large subclass of nonlocal realist theories, see e.g. this Zeilinger et al. 2007 paper:
http://arxiv.org/abs/0704.2529
Of course what you write is completely false. The non-relativistic de Brogie/Bohm theory makes exactly the same empirical predictions as standard non-relativistic quantum mechanics, and other versions (such as the Bell-type quantum field theory) can recover the predictions of QFT. The paper cited does not even claim to rule out the de Broglie/Bohm theory as it does not fall in the “large subclass”. The subclass may be large, but it does not contain the most well-studied and detailed theories. So the paper has no bearing on the point.
Lubos, I think, any program for simulations of quantum computer used nowadays is a demonstration of a “nonlocal” hidden variable model…
Right, except that any such program needs to infinitely accurately fine-tune infinitely many parameters to produce a Lorentz-invariant theory. Each new type of degree of freedom that would be added would require a new infinite fine-tuning. That’s how one may find out that it’s just a simulation, not the real deal. As the real deal, it is an infinitely^infinitely fine-tuned, and therefore infinitely unlikely, explanation. It’s less likely than the creationist description of the origin of species. You may believe it but it is not rational to believe it.
I mean only experiments about “discrete quantum variables”, yet even in continuous case there are some subtleties in such reasoning due to finite precision of our measurements.
There is no need for fine-tuning once there can exist quite simple derivations of relativistic symmetry in theories which have no fundamental relativistic symmetry, for example as a consequence of action equals reaction symmetry in my generalization of the Lorentz ether to gravity, see https://ilja-schmelzer.de/gravity/derivationEEP.php
Hi Shaun,
Sorry if I wasn’t clear: it is not that the experiments aren’t complicated, but the point that ruling out locality is not the same as ruling out either “hidden variables” or even determinism. I think we completely agree about this.
Your suggestion that the wavefunction itself be considered a “non-local hidden variable” is well taken. Bell would agree: the wavefunction is “hidden” in the sense that it cannot be directly observed but is rather inferred. Unfortunately, I think that the historical precedent for the use of the term is set. When EPR argued that the quantum description (wave function) is not complete, it became usual to call any theory that postulates something besides the wavefunction a “hidden variables” theory, even if the additionally postulated things are manifest rather than hidden. By this usage, de Broglie/Bohm is a “hidden variables” theory, so one might get the false impression that these experiments somehow refute the theory.
Tim, we are definitely in agreement that these experiments don’t rule out all “hidden variables” or determinism. Moreover, the experiments don’t say anything about non-local hidden variable theories, such as the de Broglie/Bohm interpretation that you’ve mentioned. Your point is well taken, and at this point, it comes down to terminology. Implicit in my description of “hidden variables” was the word “local.” However, I see why you take issue with that. There’s a fine line between bogging a post down with jargon and being precise. One reason for not mentioning non-local hidden variable theories is that I basically see them as extensions or interpretations of quantum mechanics. Beyond the de Broglie/Bohm theory, another example is Yakir Aharonov’s Time Symmetric Quantum Mechanics, which you might find interesting.
Excellent! We could have a nice discussion about what an extension or interpretation of QM is, but that’s for another time. I was just afraid that some readers might get the wrong impression.
Just to add more about terminology, the use of “local” is also misleading. Imagine a hidden variable theory where all objects are well localized in space, the speed of information transfer is finite, but is simply much larger than c. What would be non-local there? Nothing. But if one uses “local” instead of “Einstein-local”, one would have to name that theory “non-local”.
While such local theories cannot give exactly the same results as quantum theory, all what one could refute using the analog of Bell inequality violations for larger speeds would be some particular larger values of the limiting speed. The general idea that there exists some (however large) such limiting speed will remain viable too.
A quick question only tangentially related to the topic: Why can’t the delay choice experiment setup be used to transmit information faster than light?
Consider the following though experiment: Let’s say we have a satellite in outer space that has a built in system to analyze photon diffraction patterns, and that is currently 8 light days away from us. We constantly beam it with pulses of photons which made go through a double slit system with both slits open, and we program it so that if the detected diffraction patter changes, the satellite should do X (increase speed, decrease speed, etc) .
So here is the thing, let’s suppose that we send a pulse 7 days ago. It still has a day to reach the satellite, since the free space between the slit and the detector is 8 light days long. Now, on earth, we close one of the slits. When it arrives to the satellite the next day, due to the consequences of the Wheeler’s experiment, the resulting patter formed by that pulse will be different than those resulting of the pulses that were send previously, so the satellite would detect a change on it and do what it was programmed to do.
The net result would be that we were able to manipulate something 8 light days away with only one day of delay, thus technically letting us send “information” a lot faster than we should if we consider the limits imposed by the laws of relativity.
I did consult a couple of my professors on the topic before asking this here, but turns out no one seems to know enough about Wheeler’s experiment to provide me with a reason of why something like this couldn’t happen. If it isn’t much of a bother and if you were actually able to understand my point in despite of my tourist-tier English , would you mind explaining to me why this is wrong?
I cannot wash away the feeling that tells me that I should had flunked my undergrad courses in Quantum Mechanics for being unable to see at once why this is impossible.
Disclaimer: I have not studied physics at degree level and it is not my profession.
To answer your question, I believe that the principle of the delayed choice experiment is that once the photon has passed through the slit, a choice can be made at the current location of the photon whether or not to observe (measure) the photon or not. This then appears to have an effect on how the photon passed through the slits originally. I do not believe that closing the slit once the photon has passed is part of the experiment or has any bearing on photons which went through previously.
The crucial part of this experiment as regards your question is that the choice whether or not to measure the photon must always occur at the point at which the photon currently is. To take your specific example, this means that the decision would have to be made at a location 7 light days from earth, 1 light day from the satellite. The information from this decision would then take the expected 1 light day to reach the satellite.
Reblogged this on IISER Mohali and commented:
Hidden Variable theories in danger!
Shaun
The title, though not the body, of the post implies that hidden-variable theories generally have been discounted. However all these results only limit local hidden variable solutions, not non-local hidden-variable (NLHV) theories. This is not contentious, though often overlooked, and the post narrowly avoids making the same error.
It is worth picking up on this, if only because the greatest opportunities for breakthrough are in the extremes which others have thought barren. Specifically, it is still possible that non-local hidden-variable (NLHV) solutions might exist, including some that are different to the de Broglie-Bohm theory, e.g. http://physicsessays.org/doi/abs/10.4006/0836-1398-25.1.132. See also De Zela ‘A non-local hidden-variable model that violates Leggett-type inequalities’, 2008; Laudisa ‘Non-Local Realistic Theories and the Scope of the Bell Theorem’, 2008
Dear Dirk,
Have you had a chance to read Colbeck and Renner’s “No extension of quantum theory can have improved predictive power”, in Nature Communications (2011)? If yes, what do you think of their argument that quantum theory is complete?
Pingback: The deeper mystery of matter « Cordus
Pingback: Funny Things Happen When Space And Time Vanish » Giggles Land
“Modeling the singlet state with local hidden variables”
Supposedly that is impossible, however, Bell considered that A and B mapped into +/-1. That need not be the case. A measurement device for these types of experiments has 2 channels. Channel 1 goes ‘click’ if it detects a particle or does not click otherwise. One is free to assign any numeric structure to that ‘click’. Consider assigning to the click the 2-vector (n1,0). When the second channel clicks one can assign to it the 2-vector (0, n2). The clicks will be equally distributed between channel 1 and 2 and hence the mean will be 1/2 (n1, n2). Removing the mean from the data will cause detector 1 to respond with 1/2(n1, -n2), and detector 2 to respond with 1/2(-n1, n2) which is the negative of channel 1. The values of n1 and n2 are arbitrary and have not yet been specified. Make them equal to (a1, -a2) and -(a1, -a2) where ‘a’ is the orientation of Alice’s measurement device whose 3rd (zth) component is taken to be zero. We can now do the same for Bob so that his data looks like (b1, -b2) or -(b1, -b2). Define the response of a device as A(a,lambda)= (a1, -a2)(lambda) where lambda is now a scalar real valued random variable. Do the same for Bob but use a negative lambda since we are dealing with the singlet state. B(b,lambda) = (b1, -b1)(-lambda). The mean of lambda is zero. Its square is equal to 1. We now define the correlation between A and B by taking the inner product of A with B and then averaging over all observations in a sample. r = = -= – = -a.b, the quantum mechanical result.
Now some of you are undoubtedly thinking that I cheated by including the orientation of the measurement devices in the data. But I would argue that that is exactly what quantum mechanics does by using the Pauli spin matrices sigma(a) = ax sigmax + ay sigmay + az sigmaz and similarly for the operator with b. Quantum correlation is then where the operators act on different particles. So I am claiming that I am not cheating. If I am cheating then so is quantum mechanics.
I post this here to be critical feedback. Be as rigorous as need be.
Best regards,
Douglas G. Danforth, Ph.D.
hmm, I see part of my post was garbled. Ah, probably html thought my brackets were significant ok. Try again r = left angle bracket ATB right angle bracket = -(a1b1+a2b2) = -a.b.
Pingback: Funny Things Happen When Space And Time Vanish | Cool Stuff Funny Pictures & Other Things
ジン 腕時計
Hello to every body, it’s my first pay a quick visit of this blog;
this website includes awesome and actually fine information in support of
readers.
“Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons” by Marissa Giustina et. al was published in PRL 115, 250401 (2015) PHYSICAL REVIEW LETTERS week ending 18 DECEMBER 2015. The violation of the CH-Eberhard inequality is miniscule (1 millionth) BUT the probability of that happening for a classical system is even smaller (11 standard deviations). Hence it is claimed two loopholes are closed at the same time.
Pingback: Fear Of Not Knowing – AKANews – Featured Articles
Pingback: Fear of Not Knowing | Science and Nonduality
Wow, such a blog and post!