Author Archives: Dominik Hangleiter

What is next in quantum advantage?

Posted on by
1

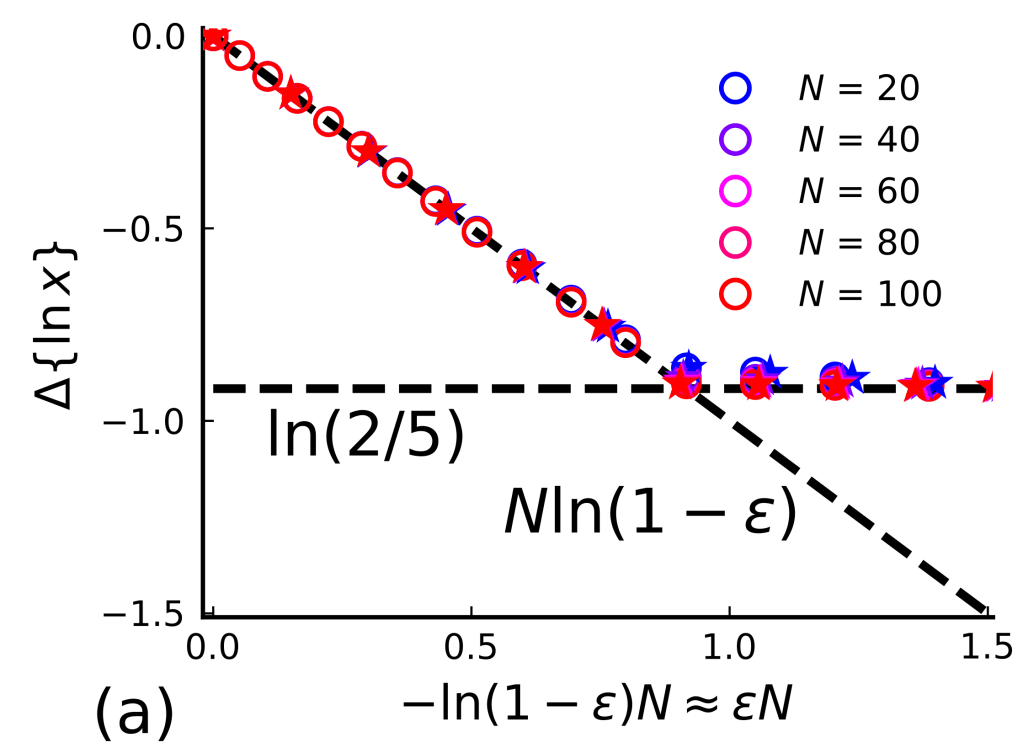
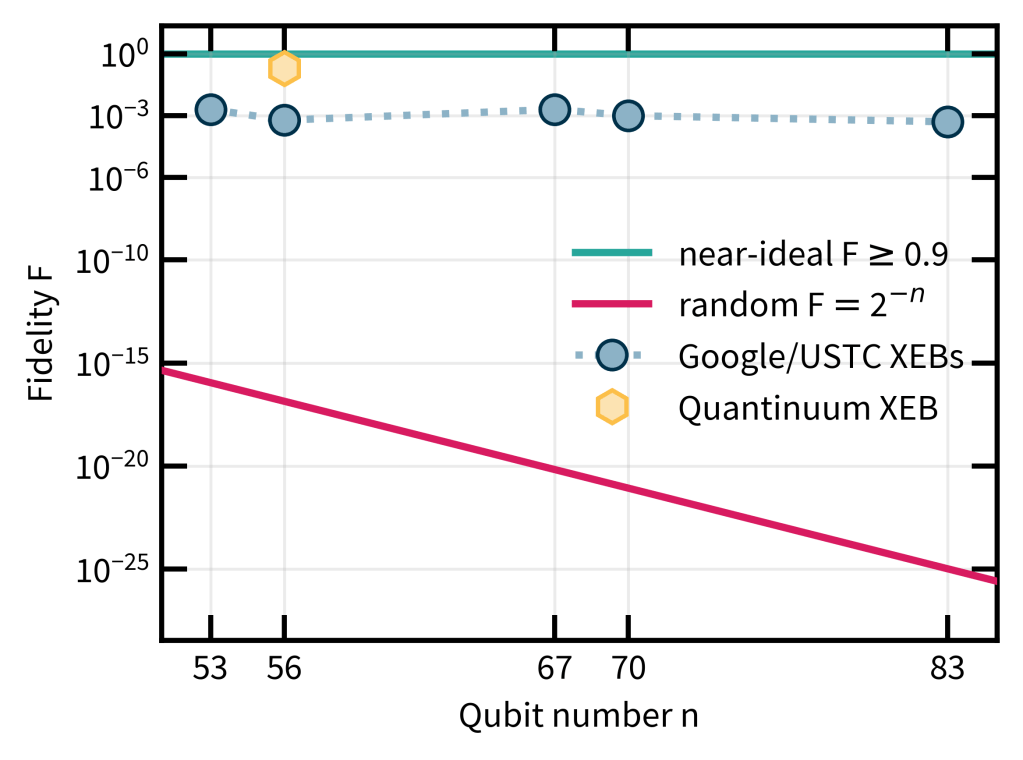
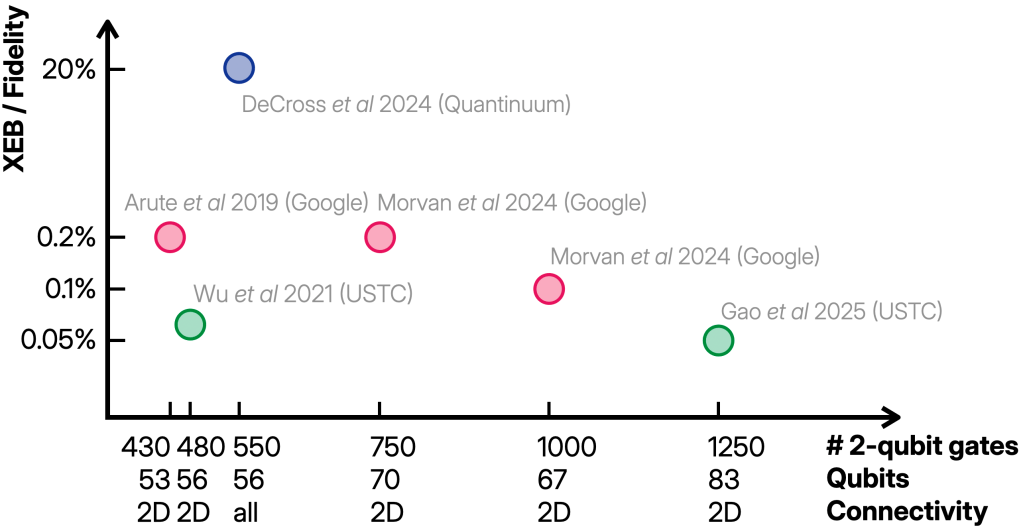
We are now at an exciting point in our process of developing quantum computers and understanding their computational power: It has been demonstrated that quantum computers can outperform classical ones (if you buy my argument from Parts 1 and 2 of this mini series). And it has been demonstrated that quantum fault-tolerance is possible for at least a few logical qubits. Together, these form the elementary building blocks of useful quantum computing.

And yet: the devices we have seen so far are still nowhere near being useful for any advantageous application in, say, condensed-matter physics or quantum chemistry, which is where the promise of quantum computers lies.

So what is next in quantum advantage?

This is what this third and last part of my mini-series on the question “Has quantum advantage been achieved?” is about.

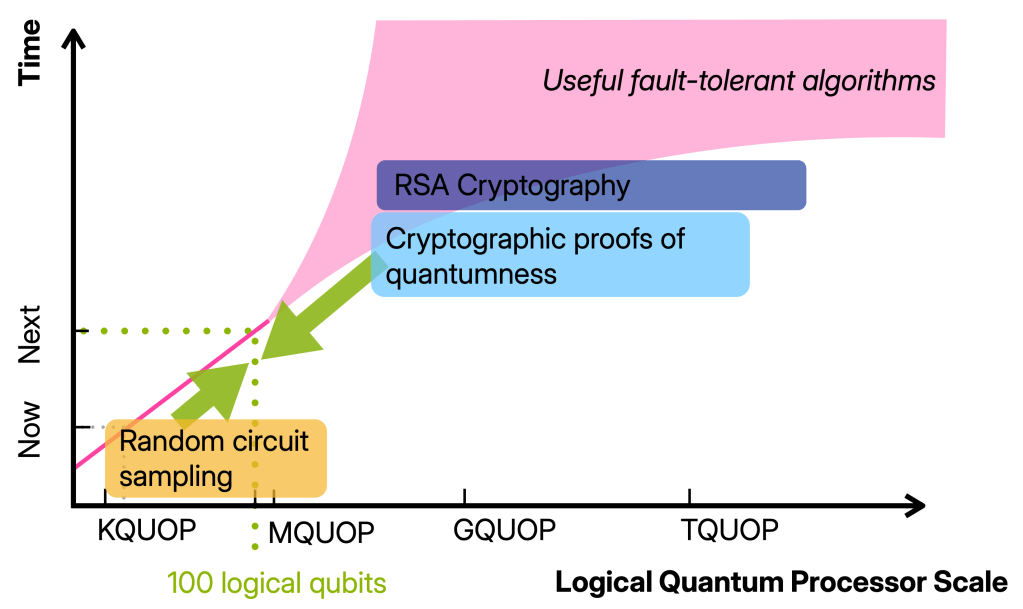
The 100 logical qubits regime
I want to have in mind the regime in which we have 100 well-functioning logical qubits, so 100 qubits on which we can run maybe 100 000 gates.

Building devices operating in this regime will require thousand(s) of physical qubits and is therefore well beyond the proof-of-principle quantum advantage and fault-tolerance experiments that have been done. At the same time, it is (so far) still one or more orders of magnitude away from any of the first applications such as simulating, say, the Fermi-Hubbard model or breaking cryptography. In other words, it is a qualitatively different regime from the early fault-tolerant computations we can do now. And yet, there is not a clear picture for what we can and should do with such devices.

The next milestone: classically verifiable quantum advantage

In this post, I want to argue that a key milestone we should aim for in the 100 logical qubit regime is classically verifiable quantum advantage. Achieving this will not only require the jump in quantum device capabilities but also finding advantage schemes that allow for classical verification using these limited resources.

Why is it an interesting and feasible goal and what is it anyway?

To my mind, the biggest weakness of the RCS experiments is the way they are verified. I discussed this extensively in the last posts—verification uses XEB which can be classically spoofed, and only actually measured in the simulatable regime. Really, in a quantum advantage experiment I would want there to be an efficient procedure that will without any reasonable doubt convince us that a computation must have been performed by a quantum computer when we run it. In what I think of as classically verifiable quantum advantage, a (classical) verifier would come up with challenge circuits which they would then send to a quantum server. These would be designed in such a way that once the server returns classical samples from those circuits, the verifier can convince herself that the server must have run a quantum computation.

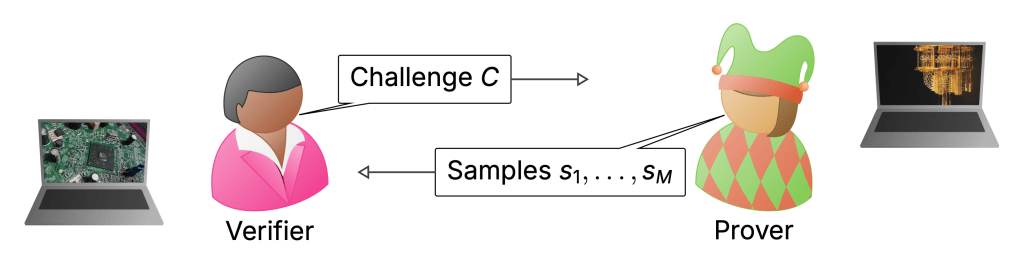
The theoretical computer scientist’s cartoon of verifying a quantum computer.

This is the jump from a physics-type experiment (the sense in which advantage has been achieved) to a secure protocol that can be used in settings where I do not want to trust the server and the data it provides me with. Such security may also allow a first application of quantum computers: to generate random numbers whose genuine randomness can be certified—a task that is impossible classically.

Here is the problem: On the one hand, we do know of schemes that allow us to classically verify that a computer is quantum and generate random numbers, so called cryptographic proofs of quantumness (PoQ). A proof of quantumness is a highly reliable scheme in that its security relies on well-established cryptography. Their big drawback is that they require a large number of qubits and operations, comparable to the resources required for factoring. On the other hand, the computations we can run in the advantage regime—basically, random circuits—are very resource-efficient but not verifiable.

The 100-logical-qubit regime lies right in the middle, and it seems more than plausible that classically verifiable advantage is possible in this regime. The theory challenge ahead of us is to find it: a quantum advantage scheme that is very resource-efficient like RCS and also classically verifiable like proofs of quantumness.

To achieve verifiable advantage in the 100-logical-qubit regime we need to close the gap between random circuit sampling and proofs of quantumness.

With this in mind, let me spell out some concrete goals that we can achieve using 100 logical qubits on the road to classically verifiable quantum advantage.

1. Demonstrate fault-tolerant quantum advantage

Before we talk about verifiable advantage, the first experiment I would like to see is one that combines the two big achievements of the past years, and shows that quantum advantage and fault-tolerance can be achieved simultaneously. Such an experiment would be similar in type to the RCS experiments, but run on encoded qubits with gate sets that match that encoding. During the computation, noise would be suppressed by correcting for errors using the code. In doing so, we could reach the near-perfect regime of RCS as opposed to the finite-fidelity regime that current RCS experiments operate in (as I discussed in detail in Part 2).

Random circuits with a quantum advantage that are particularly easy to implement fault-tolerantly are so-called IQP circuits. In those circuits, the gates are controlled-NOT gates and diagonal gates, so rotations Z(θ,z)Z(\theta,z), which just add a phase to a basis state |x⟩\ket x as Z(θ,z)|x⟩=exp⁡(iθz⋅x)|x⟩Z(\theta, z) \ket x = \exp(i \theta \, z \cdot x) \ket x. The only “quantumness” comes from the fact that each input qubit is in the superposition state |+⟩=|0⟩+|1⟩\ket + = \ket 0 + \ket 1, and that all qubits are measured in the XX basis. This is an example of an example of an IQP circuit:

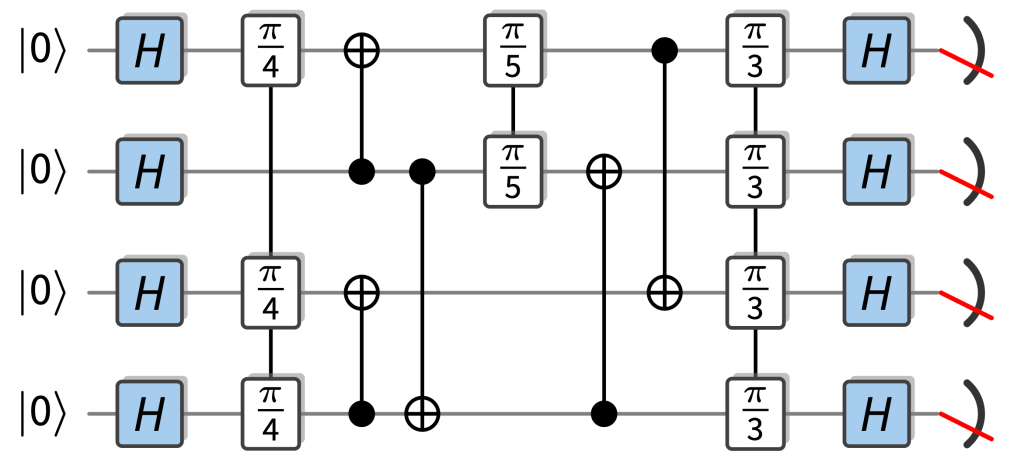
An IQP circuit starts from the all-|0⟩\ket 0 state by applying a Hadamard transform, followed by IQP gates (in this case Z(π/4,1011)Z(\pi/4,1011), some CNOT gates, Z(π/5,1100)Z(\pi/5,1100), some CNOT gates, Z(π/3,1111)Z(\pi/3,1111)) and ends in a measurement in the Hadamard basis.

As it so happens, IQP circuits are already really well understood since one of the first proposals for quantum advantage was based on IQP circuits (VerIQP1), and for a lot of the results in random circuits, we have precursors for IQP circuits, in particular, their ideal and noisy complexity (SimIQP). This is because their near-classical structure makes them relatively easy to study. Most importantly, their outcome probabilities are simple (but exponentially large) sums over phases eiθe^{i \theta } that can just be read off from which gates are applied in the circuit and we can use well-established classical techniques like Boolean analysis and coding theory to understand those.

IQP gates are natural for fault-tolerance because there are codes in which all the operations involved can be implemented transversally. This means that they only require parallel physical single- or two-qubit gates to implement a logical gate rather than complicated fault-tolerant protocols which are required for universal circuits. This is in stark contrast to universal circuit which require resource-intensive fault-tolerant protocols. Running computations with IQP circuits would also be a step towards running real computations in that they can involve structured components such as cascades of CNOT gates and the like. These show up all over fault-tolerant constructions of algorithmic primitives such as arithmetic or phase estimation circuits.

Our concrete proposal for an IQP-based fault-tolerant quantum advantage experiment in reconfigurable-atom arrays is based on interleaving diagonal gates and CNOT gates to achieve super-fast scrambling (ftIQP1). A medium-size version of this protocol was implemented by the Harvard group (LogicalExp) but with only a bit more effort, it could be performed in the advantage regime.

In those proposals, verification will still suffer from the same problems of standard RCS experiments, so what’s up next is to fix that!

2. Closing the verification loophole

I said that a key milestone for the 100-logical-qubit regime is to find schemes that lie in between RCS and proofs of quantumness in terms of their resource requirements but at the same time allow for more efficient and more convincing verification than RCS. Naturally, there are two ways to approach this space—we can make quantum advantage schemes more verifiable, and we can make proofs of quantumness more resource-efficient.

First, let’s focus on the former approach and set a more moderate goal than full-on classical verification of data from an untrusted server. Are there variants of RCS that allow us to efficiently verify that finite-fidelity RCS has been achieved if we trust the experimenter and the data they hand us?

2.1 Efficient quantum verification using random circuits with symmetries

Indeed, there are! I like to think of the schemes that achieve this as random circuits with symmetries. A symmetry is an operator SS such that the outcome state of the computation |C⟩\ket C (or some intermediate state) is invariant under the symmetry, so S|C⟩=|C⟩S \ket C =\ket C. The idea is then to find circuits CC that exhibit a quantum advantage and at the same time have symmetries that can be easily measured, say, using only single-qubit measurements or a single gate layer. Then, we can use these measurements to check whether or not the pre-measurement state respects the symmetries. This is a test for whether the quantum computer prepared the correct state, because errors or deviations from the true state would violate the symmetry (unless they were adversarially engineered).

In random circuits with symmetries, we can thus use small, well-characterized measurements whose outcomes we trust to probe whether a large quantum circuit has been run correctly. This is possible in a scenario I call the trusted experimenter scenario.

The trusted experimenter scenario
In this scenario, we receive data from an actual experiment in which we trust that certain measurements were actually and correctly performed.

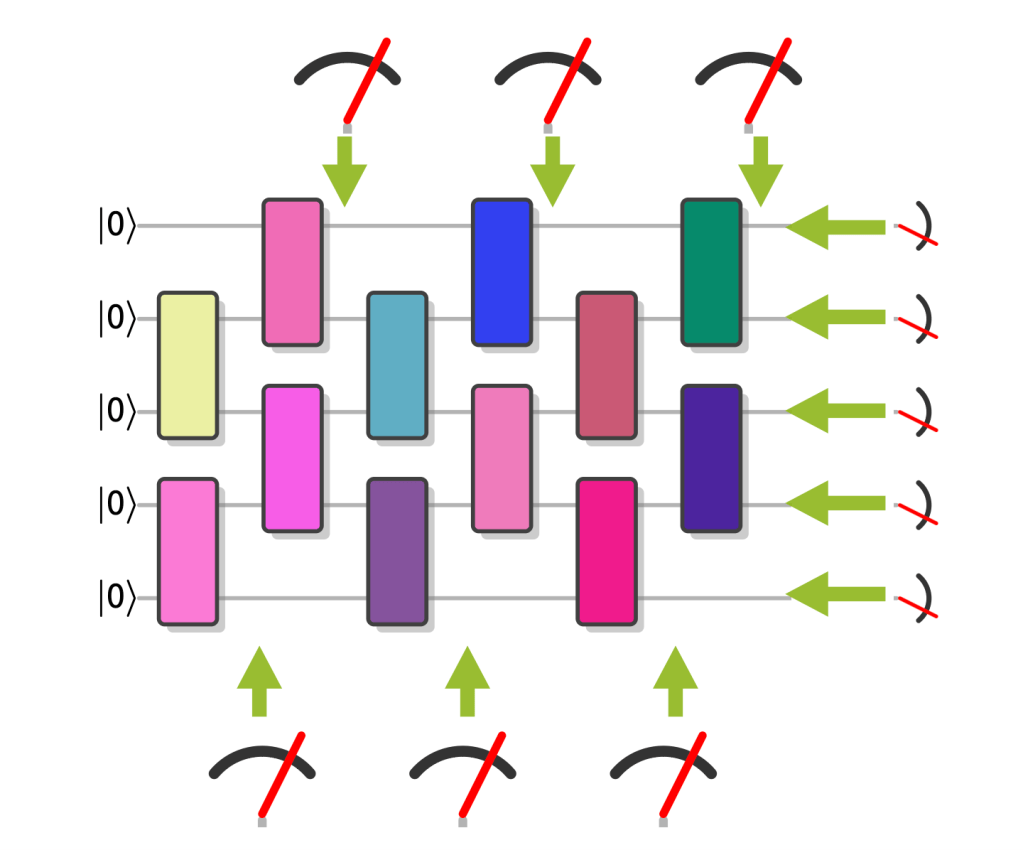
I think of random circuits with symmetries as introducing measurements in the circuit that check for errors.

Here are some examples of random circuits with symmetries, which allow for efficient verification of quantum advantage in the trusted experimenter scenario.

Graph states. My first example are locally rotated graph states (GStates). These are states that are prepared by CZ gates acting according to the edges of a graph on an initial all-|+⟩\ket + state, and a layer of single-qubit ZZ-rotations is performed before a measurement in the XX basis. (Yes, this is also an IQP circuit.) The symmetries of this circuit are locally rotated Pauli operators, and can therefore be measured using only single-qubit rotations and measurements. What is more, these symmetries fully determine the graph state. Determining the fidelity then just amounts to averaging the expectation values of the symmetries, which is so efficient you can even do it in your head. In this example, we need measuring the outcome state to obtain hard-to-reproduce samples and measuring the symmetries are done in two different (single-qubit) bases.

With 100 logical qubits, samples from classically intractable graph states on several 100 qubits could be easily generated.

Bell sampling. The drawback of this approach is that we need to make two different measurements for verification and sampling. But it would be much more neat if we could just verify the correctness of a set of classically hard samples by only using those samples. For an example where this is possible, consider two copies of the output state |C⟩\ket C of a random circuit, so |C⟩⊗|C⟩\ket C \otimes \ket C. This state is invariant under a swap of the two copies, and in fact the expectation value of the SWAP operator 𝕊\mathbb S in a noisy state preparation ρC\rho_C of |C⟩⊗|C⟩\ket C \otimes \ket C determines the purity of the state, so P=tr[ρ𝕊]P = \mathrm{tr}[ \rho \mathbb S]. It turns out that measuring all pairs of qubits in the state |C⟩⊗|C⟩\ket C \otimes \ket C in the pairwise basis of the four Bell states |σ⟩=(σ⊗𝟙)(|00⟩+|11⟩)\ket{\sigma} = (\sigma \otimes \mathbb 1) (\ket{00} + \ket{11}), where σ\sigma is one of the four Pauli matrices 𝟙,X,Y,Z\mathbb 1, X, Y, Z, this is hard to simulate classically (BellSamp). You may also observe that the SWAP operator is diagonal in the Bell basis, so its expectation value can be extracted from the Bell-basis measurements—our hard to simulate samples. To do this, we just average sign assignments to the samples according to their parity.

If the circuit is random, then under the same assumptions as those used in XEB for random circuits, the purity is a good estimator of the fidelity, so P≈F(ρC,|C⟩⊗|C⟩)P \approx F(\rho_C, \ket C \otimes \ket C). So here is an example, where efficient verification is possible directly from hard-to-simulate classical samples under the same assumptions as those used to argue that XEB equals fidelity.

With 100 logical qubits, we can achieve quantum advantage which is at least as hard as the current RCS experiments that can also be efficiently (physics-)verified from the classical data.

Fault-tolerant circuits. Finally, suppose that we run a fault-tolerant quantum advantage experiment. Then, there is a natural set of symmetries of the state at any point in the circuit, namely, the stabilizers of the code we use. In a fault-tolerant experiment we repeatedly measure those stabilizers mid-circuit, so why not use that data to assess the quality of the logical state? Indeed, it turns out that the logical fidelity can be estimated efficiently from stabilizer expectation values even in situations in which the logical circuit has a quantum advantage (SyndFid).

With 100 logical qubits, we could therefore just run fault-tolerant IQP circuits in the advantage regime (ftIQP1) and the syndrome data would allow us to estimate the logical fidelity.

In all of these examples of random circuits with symmetries, coming up with classical samples that pass the verification tests is very easy, so the trusted-experimenter scenario is crucial for this to work. (Note, however, that it may be possible to add tests to Bell sampling that make spoofing difficult.) At the same time, these proposals are very resource-efficient in that they only increase the cost of a pure random-circuit experiment by a relatively small amount. What is more, the required circuits have more structure than random circuits in that they typically require gates that are natural in fault-tolerant implementations of quantum algorithms.

Performing random circuit sampling with symmetries is therefore a natural next step en-route to both classically verifiable advantage that closes the no-efficient verification loophole, and towards implementing actual algorithms.

What if we do not want to afford that level of trust in the person who runs the quantum circuit, however?

2.2 Classical verification using random circuits with planted secrets

If we do not trust the experimenter, we are in the untrusted quantum server scenario.

The untrusted quantum server scenario
In this scenario, we delegate a quantum computation to an untrusted (presumably remote) quantum server—think of using a Google or Amazon cloud server to run your computation. We can communicate with this server using classical information.

In the untrusted server scenario, we can hope to use ideas from proofs of quantumness such as the use of classical cryptography to design families of quantum circuits in which some secret structure is planted. This secret structure should give the verifier a way to check whether a set of samples passes a certain verification test. At the same time it should not be detectable, or at least not be identifiable from the circuit description alone.

The simplest example of such secret structure could be a large peak in an otherwise flat output distribution of a random-looking quantum circuit. To do this, the verifier would pick a (random) string xx and design a circuit such that the probability of seeing xx in samples, is large. If the peak is hidden well, finding it just from the circuit description would require searching through all of the 2n2^n outcome bit strings and even just determining one of the outcome probabilities is exponentially difficult. A classical spoofer trying to fake the samples from a quantum computer would then be caught immediately: the list of samples they hand the verifier will not even contain xx unless they are unbelievably lucky, since there are exponentially many possible choices of xx.

Unfortunately, planting such secrets seems to be very difficult using universal circuits, since the output distributions are so unstructured. This is why we have not yet found good candidates of circuits with peaks, but some tries have been made (Peaks,ECPeaks,HPeaks)

We do have a promising candidate, though—IQP circuits! The fact that the output distributions of IQP circuits are quite simple could very well help us design sampling schemes with hidden secrets. Indeed, the idea of hiding peaks has been pioneered by Shepherd and Bremner (VerIQP1) who found a way to design classically hard IQP circuits with a large hidden Fourier coefficient. The presence of this large Fourier coefficient can easily be checked from a few classical samples, and random IQP circuits do not have any large Fourier coefficients. Unfortunately, for that construction and a variation thereof (VerIQP2), it turned out that the large coefficient can be detected quite easily from the circuit description (ClassIQP1,ClassIQP2).

To this day, it remains an exciting open question whether secrets can be planted in (maybe IQP) circuit families in a way that allows for efficient classical verification. Even finding a scheme with some large gap between verification and simulation times would be exciting, because it would for the first time allow us to verify a quantum computing experiment in the advantage regime using only classical computation.

Towards applications: certifiable random number generation

Beyond verified quantum advantage, sampling schemes with hidden secrets may be usable to generate classically certifiable random numbers: You sample from the output distribution of a random circuit with a planted secret, and verify that the samples come from the correct distribution using the secret. If the distribution has sufficiently high entropy, truly random numbers can be extracted from them. The same can be done for RCS, except that some acrobatics are needed to get around the problem that verification is just as costly as simulation (CertRand, CertRandExp). Again, a large gap between verification and simulation times would probably permit such certified random number generation.

The goal here is firstly a theoretical one: Come up with a planted-secret RCS scheme that has a large verification-simulation gap. But then, of course, it is an experimental one: actually perform such an experiment to classically verify quantum advantage.

Should an IQP-based scheme of circuits with secrets exist, 100 logical qubits is the regime where it should give a relevant advantage.

Three milestones

Altogether, I proposed three milestones for the 100 logical qubit regime.

  1. Perform fault-tolerant quantum advantage using random IQP circuits. This will allow an improvement of the fidelity towards performing near-perfect RCS and thus closes the scalability worries of noisy quantum advantage I discussed in my last post.
  2. Perform RCS with symmetries. This will allow for efficient verification of quantum advantage in the trusted experimenter scenario and thus make a first step toward closing the verification loophole.
  3. Find and perform RCS schemes with planted secrets. This will allow us to verify quantum advantage in the remote untrusted server scenario and presumably give a first useful application of quantum computers to generate classically certified random numbers.

All of these experiments are natural steps towards performing actually useful quantum algorithms in that they use more structured circuits than just random universal circuits and can be used to benchmark the performance of the quantum devices in an advantage regime. Moreover, all of them close some loophole of the previous quantum advantage demonstrations, just like follow-up experiments to the first Bell tests have closed the loopholes one by one.

I argued that IQP circuits will play an important role in achieving those milestones since they are a natural circuit family in fault-tolerant constructions and promising candidates for random circuit constructions with planted secrets. Developing a better understanding of the properties of the output distributions of IQP circuits will help us achieve the theory challenges ahead.

Experimentally, the 100 logical qubit regime is exactly the regime to shoot for with those circuits since while IQP circuits are somewhat easier to simulate than universal random circuits, 100 qubits is well in the classically intractable regime.

What I did not talk about

Let me close this mini-series by touching on a few things that I would have liked to discuss more.

First, there is the OTOC experiment by the Google team (OTOC) which has spawned quite a debate. This experiment claims to achieve quantum advantage for an arguably more natural task than sampling, namely, computing expectation values. Computing expectation values is at the heart of quantum-chemistry and condensed-matter applications of quantum computers. And it has the nice property that it is what the Google team called “quantum-verifiable” (and what I would call “hopefully-in-the-future-verifiable”) in the following sense: Suppose we perform an experiment to measure a classically hard expectation value on a noisy device now, and suppose this expectation value actually carries some signal, so it is significantly far away from zero. Once we have a trustworthy quantum computer in the future, we will be able to check that the outcome of this experiment was correct and hence quantum advantage was achieved. There is a lot of interesting science to discuss about the details of this experiment and maybe I will do so in a future post.

Finally, I want to mention an interesting theory challenge that relates to the noise-scaling arguments I discussed in detail in Part 2: The challenge is to understand whether quantum advantage can be achieved in the presence of a constant amount of local noise. What do we know about this? On the one hand, log-depth random circuits with constant local noise are easy to simulate classically (SimIQP,SimRCS), and we have good numerical evidence that random circuits at very low depths are easy to simulate classically even without noise (LowDSim). So is there a depth regime in between the very low depth and the log-depth regime in which quantum advantage persists under constant local noise? Is this maybe even true in a noise regime that does not permit fault-tolerance (see this interesting talk)? In the regime in which fault-tolerance is possible, it turns out that one can construct simple fault-tolerance schemes that do not require any quantum feedback, so there are distributions that are hard to simulate classically even in the presence of constant local noise.

So long, and thanks for all the fish!

I hope that in this mini-series I could convince you that quantum advantage has been achieved. There are some open loopholes but if you are happy with physics-level experimental evidence, then you should be convinced that the RCS experiments of the past years have demonstrated quantum advantage.

As the devices are getting better at a rapid pace, there is a clear goal that I hope will be achieved in the 100-logical-qubit regime: demonstrate fault-tolerant and verifiable advantage (for the experimentalists) and come up with the schemes to do that (for the theorists)! Those experiments would close the loopholes of the current RCS experiments. And they would work as a stepping stone towards actual algorithms in the advantage regime.

I want to end with a huge thanks to Spiros Michalakis, John Preskill and Frederik Hahn who have patiently read and helped me improve these posts!

References

Fault-tolerant quantum advantage

(ftIQP1) Hangleiter, D. et al. Fault-Tolerant Compiling of Classically Hard Instantaneous Quantum Polynomial Circuits on Hypercubes. PRX Quantum 6, 020338 (2025).

(LogicalExp) Bluvstein, D. et al. Logical quantum processor based on reconfigurable atom arrays. Nature 626, 58–65 (2024).

Random circuits with symmetries

(BellSamp) Hangleiter, D. & Gullans, M. J. Bell Sampling from Quantum Circuits. Phys. Rev. Lett. 133, 020601 (2024).

(GStates) Ringbauer, M. et al. Verifiable measurement-based quantum random sampling with trapped ions. Nat Commun 16, 1–9 (2025).

(SyndFid) Xiao, X., Hangleiter, D., Bluvstein, D., Lukin, M. D. & Gullans, M. J. In-situ benchmarking of fault-tolerant quantum circuits.
I. Clifford circuits. arXiv:2601.21472
II. Circuits with a quantum advantage. (coming soon!)

Verification with planted secrets

(PoQ) Brakerski, Z., Christiano, P., Mahadev, U., Vazirani, U. & Vidick, T. A Cryptographic Test of Quantumness and Certifiable Randomness from a Single Quantum Device. in 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS) 320–331 (2018).

(VerIQP1) Shepherd, D. & Bremner, M. J. Temporally unstructured quantum computation. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 465, 1413–1439 (2009).

(VerIQP2) Bremner, M. J., Cheng, B. & Ji, Z. Instantaneous Quantum Polynomial-Time Sampling and Verifiable Quantum Advantage: Stabilizer Scheme and Classical Security. PRX Quantum 6, 020315 (2025).

(ClassIQP1) Kahanamoku-Meyer, G. D. Forging quantum data: classically defeating an IQP-based quantum test. Quantum 7, 1107 (2023).

(ClassIQP2) Gross, D. & Hangleiter, D. Secret-Extraction Attacks against Obfuscated Instantaneous Quantum Polynomial-Time Circuits. PRX Quantum 6, 020314 (2025).

(Peaks) Aaronson, S. & Zhang, Y. On verifiable quantum advantage with peaked circuit sampling. arXiv:2404.14493

(ECPeaks) Deshpande, A., Fefferman, B., Ghosh, S., Gullans, M. & Hangleiter, D. Peaked quantum advantage using error correction. arXiv:2510.05262

(HPeaks) Gharibyan, H. et al. Heuristic Quantum Advantage with Peaked Circuits. arXiv:2510.25838

Certifiable random numbers

(CertRand) Aaronson, S. & Hung, S.-H. Certified Randomness from Quantum Supremacy. in Proceedings of the 55th Annual ACM Symposium on Theory of Computing 933–944 (Association for Computing Machinery, New York, NY, USA, 2023).

(CertRandExp) Liu, M. et al. Certified randomness amplification by dynamically probing remote random quantum states. arXiv:2511.03686

OTOC

(OTOC) Abanin, D. A. et al. Observation of constructive interference at the edge of quantum ergodicity. Nature 646, 825–830 (2025).

Noisy complexity

(SimIQP) Bremner, M. J., Montanaro, A. & Shepherd, D. J. Achieving quantum supremacy with sparse and noisy commuting quantum computations. Quantum 1, 8 (2017).

(SimRCS) Aharonov, D., Gao, X., Landau, Z., Liu, Y. & Vazirani, U. A polynomial-time classical algorithm for noisy random circuit sampling. in Proceedings of the 55th Annual ACM Symposium on Theory of Computing 945–957 (2023).

(LowDSim) Napp, J. C., La Placa, R. L., Dalzell, A. M., Brandão, F. G. S. L. & Harrow, A. W. Efficient Classical Simulation of Random Shallow 2D Quantum Circuits. Phys. Rev. X 12, 021021 (2022).

Has quantum advantage been achieved? Part 2: Considering the evidence

Posted on by
7

Welcome back to: Has quantum advantage been achieved?

In Part 1 of this mini-series on quantum advantage demonstrations, I told you about the idea of random circuit sampling (RCS) and the experimental implementations thereof. In this post, Part 2 out of 3, I will discuss the arguments and evidence for why I am convinced that the experiments demonstrate a quantum advantage.

Recall from Part 1 that to assess an experimental quantum advantage claim we need to check three criteria:

  1. Does the experiment correctly solve a computational task?
  2. Does it achieve a scalable advantage over classical computation?
  3. Does it achieve an in-practice advantage over the best classical attempt at solving the task?

What’s the issue?

When assessing these criteria for the RCS experiments there is an important problem: The early quantum computers we ran them on were very far from being reliable and the computation was significantly corrupted by noise. How should we interpret this noisy data? Or more concisely:

  1. Is random circuit sampling still classically hard even when we allow for whatever amount of noise the actual experiments had?
  2. Can we be convinced from the experimental data that this task has actually been solved?

I want to convince you today that we have developed a very good understanding of these questions that gives a solid underpinning to the advantage claim. Developing that understanding required a mix of methodologies from different areas of science, including theoretical computer science, algorithm design, and physics and has been an exciting journey over the past years.

The noisy sampling task

Let us start by answering the base question. What computational task did the experiments actually solve?

Recall that, in the ideal RCS scenario, we are given a random circuit CC on nnqubits and the task is to sample from the output distribution of the state obtained |C⟩\ket C from applying the circuit CC to a simple reference state. The output probability distribution of this state is determined by the Born rule when I measure every qubit in a fixed choice of basis.

Now what does a noisy quantum computer do when I execute all the gates on it and apply them to its state? Well, it prepares a noisy version ρC\rho_ C of the intended state |C⟩\ket C and once I measure the qubits, I obtain samples from the output distribution of that noisy state.

We should not make the task dependent on the specifics of that state or the noise that determined it, but we can define a computational task based on this observation by fixing how accurate that noisy state preparation is. The natural way to do this is to use the fidelity

F(C)=⟨C|ρC|C⟩, F(C) = \bra C \rho_C \ket C,

which is just the overlap between the ideal state and the noisy state. The fidelity is 1 if the noisy state is equal to the ideal state, and 0 if it is perfectly orthogonal to it.

Finite-fidelity random circuit sampling
Given a typical random circuit CC, sample from the output distribution of any quantum state whose fidelity with the ideal output state |C⟩\ket C is at least δ\delta.

Note that finite-fidelity RCS does not demand success for every circuit, but only for typical circuits from the random circuit ensemble. This matches what the experiments do: they draw random circuits and need the device to perform well on the overwhelming majority of those draws. Accordingly, when the experiments quote a single number as “fidelity”, it is really the typical (or, more precisely, circuit-averaged) fidelity that I will just call FF.

The noisy experiments claim to have solved finite-fidelity RCS for values of δ\delta around 0.1%. What is more, they consistently achieve this value even as the circuit sizes are increased in the later experiments. Both the actual value and the scaling will be important later.

What is the complexity of finite-fidelity RCS?

Quantum advantage of finite-fidelity RCS

Let’s start off by supposing that the quantum computation is (nearly) perfectly executed, so the required fidelity δ\delta is quite large, say, 90%. In this scenario, we have very good evidence based on computational complexity theory that there is a scalable and in-practice quantum advantage for RCS. This evidence is very strong, comparable to the evidence we have for the hardness of factoring and simulating quantum systems. The intuition behind it is that quantum output probabilities are extremely hard to compute because of a mechanism behind quantum advantages: destructive interference. If you are interested in the subtleties and the open questions, take a look at our survey.

The question is now, how far down in fidelity this classical hardness persists? Intuitively, the smaller we make δ\delta, the easier finite-fidelity RCS should become for a classical algorithm (and a quantum computer, too), since the freedom we have in deviating from the ideal state in our simulation becomes larger and larger. This increases the possibility of finding a state that turns out to be easy to simulate within the fidelity constraint.

Somewhat surprisingly, though, finite-fidelity RCS seems to remain hard even for very small values of δ\delta. I am not aware of any efficient classical algorithm that achieves the finite-fidelity task for δ\delta significantly away from the baseline trivial value of 2−n2^{-n}. This is the value a maximally mixed or randomly picked state achieves because a random state has no correlation with the ideal state (or any other state), and 2−n2^{-n} is exactly what you expect in that case (while 0 would correspond to perfect anti-correlation).

One can save some classical runtime compared to solving near-ideal RCS by exploiting a reduced fidelity, but the costs remain exponential. To classically solve finite-fidelity RCS, the best known approaches are reported in the papers that performed classical simulations of finite-fidelity RCS with the parameters of the first Google and USTC experiment (classSim1, classSim2). To achieve this, however, they needed to approximately simulate the ideal circuits at an immense cost. To the best of my knowledge, all but those first two experiments are far out of reach for these algorithms.

Getting the scaling right: weak noise and low depth

So what is the right value of δ\delta at which we can hope for a scalable and in-practice advantage of RCS experiments?

When thinking about this question, it is helpful to keep a model of the circuit in mind that a noisy experiment runs. So, let us consider a noisy circuit on nn qubits with dd layers of gates and single-qubit noise of strength ε\varepsilon on every qubit in every layer. In this scenario, the typical fidelity with the ideal state will decay as F∼exp⁡(−εnd)F \sim \exp(- \varepsilon n d).

Any reasonably testable value of the fidelity needs to scale as 1/𝗉𝗈𝗅𝗒(n)1/\mathsf{poly}(n), since eventually we need to estimate the average fidelity FF from the experimental samples and this typically requires at least 1/F21/F^2 samples, so exponentially small fidelities are experimentally invisible. The polynomial fidelity δ\delta is also much closer to the near-ideal scenario (δ≥\delta \geq90%) than the trivial scenario (δ=2−n\delta = 2^{-n}). While we cannot formally pin this down, the intuition behind the complexity-theoretic evidence for the hardness of near-ideal RCS persists into the δ∼1/𝗉𝗈𝗅𝗒(n)\delta \sim 1/\mathsf{poly}(n) regime: to sample up to such high precision, we still need a reasonably accurate estimate of the ideal probabilities, and getting this is computationally extremely difficult. Scalable quantum advantage in this regime is therefore a pretty safe bet.

How do the parameters of the experiment and the RCS instances need to scale with the number of qubits nn to experimentally achieve the fidelity regime? The limit to consider is one in which the noise rate decreases with the number of qubits, while the circuit depth is only allowed to increase very slowly. It depends on the circuit architecture, i.e., the choice of circuit connectivity, and the gate set, through a constant cAc_A as I will explain in more detail below.

Weak-noise and low-depth scaling
(Weak noise) The local noise rate of the quantum device scales as ε<cA/n\varepsilon \lt c_A/n.
(Low depth) The circuit depth scales as d≲log⁡nd \lesssim \log n.

This limit is such that we have a scaling of the fidelity as F≳n−cF \gtrsim n^{-c} for some constant cc. It is also a natural scaling limit for noisy devices whose error rates gradually improve through better engineering. You might be worried about the fact that the depth needs to be quite low but it turns out that there is a solid quantum advantage even for log⁡(n)\log(n)-depth circuits.

The precise definition of the weak-noise regime is motivated by the following observation. It turns out to be crucial for assessing the noisy data from the experiment.

Fidelity versus XEB: a phase transition

Remember from Part 1 that the experiments measured a quantity called the cross-entropy benchmark (XEB)

χ=22n𝔼C𝔼xpC(x)−1,\chi = 2^{2n} \mathbb E_C \mathbb E_{x} p_C(x) -1 ,

The XEB averages the ideal probabilities pC(x)p_C(x) corresponding to the sampled outcomes xx from experiments on random circuits CC. Thus, it correlates the experimental and ideal output distributions of those random circuits. You can think of it as a “classical version” of the fidelity: If the experimental distribution is correct, the XEB will essentially be 1. If it is uniformly random, the XEB is 0.

The experiments claimed that the XEB is a good proxy for the circuit-averaged fidelity given by F=𝔼CF(C)F = \mathbb E_C F(C), and so we need to understand when this is true. Fortunately, in the past few years, alongside with the improved experiments, we have developed a very good understanding of this question (WN, Spoof2, PT1, PT2).

It turns out that the quality of correspondence between XEB and average fidelity depends strongly on the noise in the experimental quantum state. In fact, there is a sharp phase transition: there is an architecture-dependent constant cAc_A such that when the experimental local noise rate ε<cA/n\varepsilon < c_A/n, then the XEB is a good and reliable proxy for the average fidelity for any system size nn and circuit depth dd. This is exactly the weak-noise regime. Above that threshold, in the strong noise regime, the XEB is an increasingly bad proxy for the fidelity (PT1, PT2).

Let me be more precise: In the weak-noise regime, when we consider the decay of the XEB as a function of circuit depth dd, the rate of decay is given by εn\varepsilon n, i.e., the XEB decays as exp⁡(−εnd)\exp(- \varepsilon n d ). Meanwhile, in the strong-noise regime the rate of decay is constant, giving an XEB decay as exp⁡(−Cd)\exp(- C d) for a constant CC. At the same time, the fidelity decays as exp⁡(−εnd)\exp(- \varepsilon n d ) regardless of the noise regime. Hence, in the weak-noise regime, the XEB is a good proxy of the fidelity, while in the strong noise regime, there is an exponentially increasing gap between the XEB (which remains large) and the fidelity (which continues to decay exponentially). regardless of the noise regime.

This is what the following plot shows. We computed it from an exact mapping of the behavior of the XEB to the dynamics of a statistical-mechanics model that can be evaluated efficiently. Using this mapping, we can also compute the noise threshold cAc_A for whichever random circuit family and architecture you are interested in.

From (PT2). The yy-axis label Δ(ln⁡χ)\Delta( \ln \chi ) is the decay rate of the XEB χ\chi, N=nN=n the number of qubits and ε\varepsilon is the local noise rate.

Where are the experiments?

We are now ready to take a look at the crux when assessing the noisy data: Can we trust the reported XEB values as an estimator of the fidelity? If so, do the experiments solve finite-fidelity RCS in the solidly hard regime where δ≥1/𝗉𝗈𝗅𝗒(n)\delta \geq 1/ \mathsf{poly}(n)?

In their more recent paper (PT1), the Google team explicitly verified that the experiment is well below the phase transition, and it turns out that the first experiment was just at the boundary. The USTC experiments had comparable noise rates, and the Quantinuum experiment much better ones. Since fidelity decays as exp⁡(−εnd)\exp(-\varepsilon n d), but the reported XEB values stayed consistently around 0.1% as nn was increased, the experimental error rate ε\varepsilon of the experiments improved even better than the 1/n1/n scaling required for the weak-noise regime, namely, more like ε∼1/(nd)\varepsilon \sim 1/(nd). Altogether, the experiments are therefore in the weak-noise regime both in terms of absolute numbers relative to cA/nc_A/n and the required scaling.

Of course, to derive the transition, we made some assumptions about the noise such as that the noise is local, and that it does not depend much on the circuit itself. In the advantage experiments, these assumptions about the noise are characterized and tested. This is done through a variety of means at increasing levels of complexity, including detailed characterization of the noise in individual gates, gates run in parallel, and eventually in a larger circuit. The importance of understanding the noise shows in the fact that a significant portion of the supplementary materials of the advantage experiments is dedicated to getting this right. All of this contributes to the experimental justification for using the XEB as a proxy for the fidelity!

The data shows that the experiments solved finite-fidelity RCS for values of δ\delta above the constant value of roughly 0.1% as the experiments grew. In the following plot, I compare the experimental fidelity values to the near-ideal scenario on the one hand, and the trivial 2−n2^{-n} value on the other hand. Viewed at this scale, the values of δ\delta for which the experiment solved finite-fidelity RCS are indeed vastly closer to the near-ideal value than the trivial baseline, which should boost our confidence that reproducing samples at a similar fidelity is extremely challenging.

The phase transition matters!

You might be tempted to say: “Well, but is all this really so important? Can’t I just use XEB and forget all about fidelity?”

The phase transition shows why that would change the complexity of the problem: in the strong-noise regime, XEB can stay high even when fidelity is exponentially small. And indeed, this discrepancy can be exploited by so-called spoofers for the XEB. These are efficient classical algorithms which can be used to succeed at a quantum advantage test even though they clearly do not achieve the intended advantage. These spoofers (Spoof1, Spoof2) can achieve high XEB scores comparable to those of the experiments and scaling like exp⁡(−cd)\exp(-cd) in the circuit depth dd for some constant cc.

Their basic idea is to introduce strong, judiciously chosen noise at specific circuit locations that has the effect of breaking up the simulation task up into smaller, much easier components, but at the same time still gives a high XEB score. In doing so, they exploit the strong-noise regime in which the XEB is a really bad proxy for the fidelity. This allows them to sample from states with exponentially low fidelity while achieving a high XEB value.

The discovery of the phase transition and the associated spoofers highlights the importance of modeling when assessing—and even formulating—the advantage claim based on noisy data.

But we can’t compute the XEB!

You might also be worried that the experiments did not actually compute the XEB in the advantage regime because to estimate it they would have needed to compute ideal probabilities—a task that is hard by definition of the advantage regime. Instead, they used a bunch of different ways to extrapolate the true XEB from XEB proxies (proxy of a proxy of the fidelity). Is this is a valid way of getting an estimate of the true XEB?

It totally is! Different extrapolations—from easy-to-simulate to hard-to-simulate, from small system to large system etc—all gave consistent answers for the experimental XEB value of the supremacy circuits. Think of this as having several lines that cross in the same point. For that crossing to be a coincidence, something crazy, conspiratorial must happen exactly when you move to the supremacy circuits from different directions. That is why it is reasonable to trust the reported value of the XEB.

That’s exactly how experiments work!

All of this is to say that establishing that the experiments correctly solved finite-fidelity RCS and therefore show quantum advantage involved a lot of experimental characterization of the noise as well as theoretical work to understand the effects of noise on the quantity we care about—the fidelity between the experimental and ideal states.

In this respect (and maybe also in the scale of the discovery), the quantum advantage experiments are similar to the recent experiments reporting discovery of the Higgs boson and gravitational waves. While I do not claim to understand any of the details, what I do understand is that in both experiments, there is an unfathomable amount of data that could not be interpreted without preselection and post-processing of the data, theories, extrapolations and approximations that model the experiment and measurement apparatus. All of those enter the respective smoking-gun plots that show the discoveries.

If you believe in the validity of experimental physics methodology, you should therefore also believe in the type of evidence underlying experimental claim of the quantum advantage demonstrations: that they sampled from the output distribution of a quantum state with the reported fidelities.

Put succinctly: If you believe in the Higgs boson and gravitational waves, you should probably also believe in the experimental demonstration of quantum advantage.

What are the counter-arguments?

The theoretical computer scientist

“The weak-noise limit is not physical. The appropriate scaling limit is one in which the local noise rate of the device is constant while the system size grows, and in that case, there is a classical simulation algorithm for RCS (SimIQP, SimRCS).”

In theoretical computer science, scaling of time or the system size in the input size is considered very natural: We say an algorithm is efficient if its runtime and space usage only depend polynomially on the input size.

But all scaling arguments are hypothetical concepts, and we only care about the scaling at relevant sizes. In the end, every scaling limit is going to hit the wall of physical reality—be it the amount of energy or human lifetime that limits the time of an algorithm, or the physical resources that are required to build larger and larger computers. To keep the scaling limit going as we increase the size of our computations, we need innovation that makes the components smaller and less noisy.

At the scales relevant to RCS, the 1/n1/n scaling of the noise is benign and even natural. Why? Well, currently, the actual noise in quantum computers is not governed by the fundamental limit, but by engineering challenges. Realizing this limit therefore amounts to engineering improvements in the system size and noise rate that are achieved over time. Sure, at some point that scaling limit is also going to hit a fundamental barrier below which the noise cannot be improved. But we are surely far away from that limit, yet. What is more, already now logical qubits are starting to work and achieve beyond-breakeven fidelities. So even if the engineering improvements should flatten out from here onward, QEC will keep the 1/n1/n noise limit going and even accelerate it in the intermediate future.

The complexity maniac

“All the hard complexity-theoretic evidence for quantum advantage is in the near-ideal regime, but now you are claiming advantage for the low-fidelity version of that task.”

This is probably the strongest counter-argument in my opinion, and I gave my best response above. Let me just add that this is a question about computational complexity. In the end, all of complexity theory is based on belief. The only real evidence we have for the hardness of any task is the absence of an efficient algorithm, or the reduction to a paradigmatic, well-studied task for which there is no efficient algorithm.

I am not sure how much I would bet that you cannot find an efficient algorithm for finite-fidelity RCS in the regime of the experiments, but it is certainly a pizza.

The enthusiastic skeptic

“There is no verification test that just depends on the classical samples, is efficient and does not make any assumptions about the device. In particular, you cannot unconditionally verify fidelity just from the classical samples. Why should I believe the data?”

Yes, sure, the current advantage demonstrations are not device-independent. But the comparison you should have in mind are Bell tests. The first proper Bell tests of Aspect and others in the 80s were not free of loopholes. They still allowed for contrived explanations of the data that did not violate local realism. Still, I can hardly believe that anyone would argue that Bell inequalities were not violated already back then.

As the years passed, these remaining loopholes were closed. To be a skeptic of the data, people needed to come up with more and more adversarial scenarios that could explain the data. We are working on the same to happen with quantum advantage demonstrations: come up with better schemes and better tests that require less and less assumptions or knowledge about the specifics of the device.

The “this is unfair” argument

“When you chose the gates and architecture of the circuit dependent on your device, you tailored the task too much to the device and that is unfair. Not even the different RCS experiments solve exactly the same task.”

This is not really an argument against the achievement of quantum advantage but more against the particular choices of circuit ensembles in the experiments. Sure, the specific computations solved are still somewhat tailored to the hardware itself and in this sense the experiments are not hardware-independent yet, but they still solve fine computational tasks. Moving away from such hardware-tailored task specifications is another important next step and we are working on it.

In the third and last part of this mini series I will address next steps in quantum advantage that aim at closing some of the remaining loopholes. The most important—and theoretically interesting—one is to enable efficient verification of quantum advantage using less or even no specific knowledge about the device that was used, but just the measurement outcomes.

References

(survey) Hangleiter, D. & Eisert, J. Computational advantage of quantum random sampling. Rev. Mod. Phys. 95, 035001 (2023).

(classSim1) Pan, F., Chen, K. & Zhang, P. Solving the sampling problem of the Sycamore quantum circuits. Phys. Rev. Lett. 129, 090502 (2022).

(classSim2) Kalachev, G., Panteleev, P., Zhou, P. & Yung, M.-H. Classical Sampling of Random Quantum Circuits with Bounded Fidelity. arXiv.2112.15083 (2021).

(WN) Dalzell, A. M., Hunter-Jones, N. & Brandão, F. G. S. L. Random Quantum Circuits Transform Local Noise into Global White Noise. Commun. Math. Phys. 405, 78 (2024).

(PT1)vMorvan, A. et al. Phase transitions in random circuit sampling. Nature 634, 328–333 (2024).

(PT2) Ware, B. et al. A sharp phase transition in linear cross-entropy benchmarking. arXiv:2305.04954 (2023).

(Spoof1) Barak, B., Chou, C.-N. & Gao, X. Spoofing Linear Cross-Entropy Benchmarking in Shallow Quantum Circuits. in 12th Innovations in Theoretical Computer Science Conference (ITCS 2021) (ed. Lee, J. R.) vol. 185 30:1-30:20 (2021).

(Spoof2) Gao, X. et al. Limitations of Linear Cross-Entropy as a Measure for Quantum Advantage. PRX Quantum 5, 010334 (2024).

(SimIQP) Bremner, M. J., Montanaro, A. & Shepherd, D. J. Achieving quantum supremacy with sparse and noisy commuting quantum computations. Quantum 1, 8 (2017).

(SimRCS) Aharonov, D., Gao, X., Landau, Z., Liu, Y. & Vazirani, U. A polynomial-time classical algorithm for noisy random circuit sampling. in Proceedings of the 55th Annual ACM Symposium on Theory of Computing 945–957 (2023).

Has quantum advantage been achieved?

Posted on by
8

Recently, I gave a couple of perspective talks on quantum advantage, one at the annual retreat of the CIQC and one at a recent KITP programme. I started off by polling the audience on who believed quantum advantage had been achieved. Just this one, simple question.

The audience was mostly experimental and theoretical physicists with a few CS theory folks sprinkled in. I was sure that these audiences would be overwhelmingly convinced of the successful demonstration of quantum advantage. After all, more than half a decade has passed since the first experimental claim (G1) of “quantum supremacy” as the patron of this blog’s institute called the idea “to perform tasks with controlled quantum systems going beyond what can be achieved with ordinary digital computers” (Preskill, p. 2) back in 2012. Yes, this first experiment by the Google team may have been simulated in the meantime, but it was only the first in an impressive series of similar demonstrations that became bigger and better with every year that passed. Surely, so I thought, a significant part of my audiences would have been convinced of quantum advantage even before Google’s claim, when so-called quantum simulation experiments claimed to have performed computations that no classical computer could do (e.g. (qSim)).

I could not have been more wrong.

In both talks, less than half of the people in the audience thought that quantum advantage had been achieved.

In the discussions that ensued, I came to understand what folks criticized about the experiments that have been performed and even the concept of quantum advantage to begin with. But more on that later. Most of all, it seemed to me, the community had dismissed Google’s advantage claim because of the classical simulation shortly after. It hadn’t quite kept track of all the advances—theoretical and experimental—since then.

In a mini-series of three posts, I want to remedy this and convince you that the existing quantum computers can perform tasks that no classical computer can do. Let me caution, though, that the experiments I am going to talk about solve a (nearly) useless task. Nothing of what I say implies that you should (yet) be worried about your bank accounts.

I will start off by recapping what quantum advantage is and how it has been demonstrated in a set of experiments over the past few years.

Part 1: What is quantum advantage and what has been done?

To state the obvious: we are now fairly convinced that noiseless quantum computers would be able solve problems efficiently that no classical computer could solve. In fact, we have been convinced of that already since the mid-90ies when Lloyd and Shor discovered two basic quantum algorithms: simulating quantum systems and factoring large numbers. Both of these are tasks where we are as certain as we could be that no classical computer can solve them. So why talk about quantum advantage 20 and 30 years later?

The idea of a quantum advantage demonstration—be it on a completely useless task even—emerged as a milestone for the field in the 2010s. Achieving quantum advantage would finally demonstrate that quantum computing was not just a random idea of a bunch of academics who took quantum mechanics too seriously. It would show that quantum speedups are real: We can actually build quantum devices, control their states and the noise in them, and use them to solve tasks which not even the largest classical supercomputers could do—and these are very large.

What is quantum advantage?

But what exactly do we mean by “quantum advantage”. It is a vague concept, for sure. But some essential criteria that a demonstration should certainly satisfy are probably the following.

  1. The quantum device needs to solve a pre-specified computational task. This means that there needs to be an input to the quantum computer. Given the input, the quantum computer must then be programmed to solve the task for the given input. This may sound trivial. But it is crucial because it delineates programmable computing devices from just experiments on any odd physical system.
  2. There must be a scaling difference in the time it takes for a quantum computer to solve the task and the time it takes for a classical computer. As we make the problem or input size larger, the difference between the quantum and classical solution times should increase disproportionately, ideally exponentially.
  3. And finally: the actual task solved by the quantum computer should not be solvable by any classical machine (at the time).

Achieving this last criterion using imperfect, noisy quantum devices is the challenge the idea of quantum supremacy set for the field. After all, running any of our favourite quantum algorithms in a classically hard regime on these devices is completely out of the question. They are too small and too noisy. So the field had to come up with the conceivably smallest and most noise-robust quantum algorithm that has a significant scaling advantage against classical computation.

Random circuits are really hard to simulate!

The idea is simple: we just run a random computation, constructed in a way that is as favorable as we can make it to the quantum device while being as hard as possible classically. This may strike as a pretty unfair way to come up with a computational task—it is just built to be hard for classical computers without any other purpose. But: it is a fine computational task. There is an input: the description of the quantum circuit, drawn randomly. The device needs to be programmed to run this exact circuit. And there is a task: just return whatever this quantum computation would return. These are strings of 0s and 1s drawn from a certain distribution. Getting the distribution of the strings right for a given input circuit is the computational task.

This task, dubbed random circuit sampling, can be solved on a classical as well as a quantum computer, but there is a (presumably) exponential advantage for the quantum computer. More on that in Part 2.

For now, let me tell you about the experimental demonstrations of random circuit sampling. Allow me to be slightly more formal. The task solved in random circuit sampling is to produce bit strings x∈{0,1}nx \in \{0,1\}^n distributed according to the Born-rule outcome distribution

pC(x)=|⟨x|C|0⟩|2p_C(x) = | \bra x C \ket {0}|^2

of a sequence of elementary quantum operations (unitary rotations of one or two qubits at a time) which is drawn randomly according to certain rules. This circuit CC is applied to a reference state |0⟩\ket 0 on the quantum computer and then measured, giving the string xx as an outcome.

The breakthrough: classically hard programmable quantum computations in the real world

In the first quantum supremacy experiment (G1) by the Google team, the quantum computer was built from 53 superconducting qubits arranged in a 2D grid. The operations were randomly chosen simple one-qubit gates (X,Y,X+Y\sqrt X, \sqrt Y, \sqrt{X+Y}) and deterministic two-qubit gates called fSim applied in the 2D pattern, and repeated a certain number of times (the depth of the circuit). The limiting factor in these experiments was the quality of the two-qubit gates and the measurements, with error probabilities around 0.6 % and 4 %, respectively.

A very similar experiment was performed by the USTC team on 56 qubits (U1) and both experiments were repeated with better fidelities (0.4 % and 1 % for two-qubit gates and measurements) and slightly larger system sizes (70 and 83 qubits, respectively) in the past two years (G2,U2).

Using a trapped-ion architecture, the Quantinuum team also demonstrated random circuit sampling on 56 qubits but with arbitrary connectivity (random regular graphs) (Q). There, the two-qubit gates were π/2\pi/2-rotations around Z⊗ZZ \otimes Z, the single-qubit gates were uniformly random and the error rates much better (0.15 % for both two-qubit gate and measurement errors).

All the experiments ran random circuits on varying system sizes and circuit depths, and collected thousands to millions of samples from a few random circuits at a given size. To benchmark the quality of the samples, the widely accepted benchmark is now the linear cross-entropy (XEB) benchmark defined as

χ=22n𝔼C𝔼xpC(x)−1,\chi = 2^{2n} \mathbb E_C \mathbb E_{x} p_C(x) -1 ,

for an nn-qubit circuit. The expectation over CC is over the random choice of circuit and the expectation over xx is over the experimental distribution of the bit strings. In other words, to compute the XEB given a list of samples, you ‘just’ need to compute the ideal probability of obtaining that sample from the circuit CC and average the outcomes.

The XEB is nice because it gives 1 for ideal samples from sufficiently random circuits and 0 for uniformly random samples, and it can be estimated accurately from just a few samples. Under the right conditions, it turns out to be a good proxy for the many-body fidelity of the quantum state prepared just before the measurement.

This tells us that we should expect an XEB score of (1−error per gate)# gates∼c−nd(1-\text{error per gate})^{\text{\# gates}} \sim c^{- n d } for some noise- and architecture-dependent constant cc. All of the experiments achieved a value of the XEB that was significantly (in the statistical sense) far away from 0 as you can see in the plot below. This shows that something nontrivial is going on in the experiments, because the fidelity we expect for a maximally mixed or random state is 2−n2^{-n} which is less than 10−1410^{-14} % for all the experiments.

The complexity of simulating these experiments is roughly governed by an exponential in either the number of qubits or the maximum bipartite entanglement generated. Figure 5 of the Quantinuum paper has a nice comparison.

It is not easy to say how much leverage an XEB significantly lower than 1 gives a classical spoofer. But one can certainly use it to judiciously change the circuit a tiny bit to make it easier to simulate.

Even then, reproducing the low scores between 0.05 % and 0.2 % of the experiments is extremely hard on classical computers. To the best of my knowledge, producing samples that match the experimental XEB score has only been achieved for the first experiment from 2019 (PCZ). This simulation already exploited the relatively low XEB score to simplify the computation, but even for the slightly larger 56 qubit experiments these techniques may not be feasibly run. So to the best of my knowledge, the only one of the experiments which may actually have been simulated is the 2019 experiment by the Google team.

If there are better methods, or computers, or more willingness to spend money on simulating random circuits today, though, I would be very excited to hear about it!

Proxy of a proxy of a benchmark

Now, you may be wondering: “How do you even compute the XEB or fidelity in a quantum advantage experiment in the first place? Doesn’t it require computing outcome probabilities of the supposedly hard quantum circuits?” And that is indeed a very good question. After all, the quantum advantage of random circuit sampling is based on the hardness of computing these probabilities. This is why, to get an estimate of the XEB in the advantage regime, the experiments needed to use proxies and extrapolation from classically tractable regimes.

This will be important for Part 2 of this series, where I will discuss the evidence we have for quantum advantage, so let me give you some more detail. To extrapolate, one can just run smaller circuits of increasing sizes and extrapolate to the size in the advantage regime. Alternatively, one can run circuits with the same number of gates but with added structure that makes them classically simulatable and extrapolate to the advantage circuits. Extrapolation is based on samples from different experiments from the quantum advantage experiments. All of the experiments did this.

A separate estimate of the XEB score is based on proxies. An XEB proxy uses the samples from the advantage experiments, but computes a different quantity than the XEB that can actually be computed and for which one can collect independent numerical and theoretical evidence that it matches the XEB in the relevant regime. For example, the Google experiments averaged outcome probabilities of modified circuits that were related to the true circuits but easier to simulate.

The Quantinuum experiment did something entirely different, which is to estimate the fidelity of the advantage experiment by inverting the circuit on the quantum computer and measuring the probability of coming back to the initial state.

All of the methods used to estimate the XEB of the quantum advantage experiments required some independent verification based on numerics on smaller sizes and induction to larger sizes, as well as theoretical arguments.

In the end, the advantage claims are thus based on a proxy of a proxy of the quantum fidelity. This is not to say that the advantage claims do not hold. In fact, I will argue in my next post that this is just the way science works. I will also tell you more about the evidence that the experiments I described here actually demonstrate quantum advantage and discuss some skeptical arguments.

Let me close this first post with a few notes.

In describing the quantum supremacy experiments, I focused on random circuit sampling which is run on programmable digital quantum computers. What I neglected to talk about is boson sampling and Gaussian boson sampling, which are run on photonic devices and have also been experimentally demonstrated. The reason for this is that I think random circuits are conceptually cleaner since they are run on processors that are in principle capable of running an arbitrary quantum computation while the photonic devices used in boson sampling are much more limited and bear more resemblance to analog simulators.

I want to continue my poll here, so feel free to write in the comments whether or not you believe that quantum advantage has been demonstrated (by these experiments) and if not, why.

References

[G1] Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).

[Preskill] Preskill, J. Quantum computing and the entanglement frontier. arXiv:1203.5813 (2012).

[qSim] Choi, J. et al. Exploring the many-body localization transition in two dimensions. Science 352, 1547–1552 (2016). .

[U1] Wu, Y. et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 127, 180501 (2021).

[G2] Morvan, A. et al. Phase transitions in random circuit sampling. Nature 634, 328–333 (2024).

[U2] Gao, D. et al. Establishing a New Benchmark in Quantum Computational Advantage with 105-qubit Zuchongzhi 3.0 Processor. Phys. Rev. Lett. 134, 090601 (2025).

[Q] DeCross, M. et al. Computational Power of Random Quantum Circuits in Arbitrary Geometries. Phys. Rev. X 15, 021052 (2025).

[PCZ] Pan, F., Chen, K. & Zhang, P. Solving the sampling problem of the Sycamore quantum circuits. Phys. Rev. Lett. 129, 090502 (2022).