“How good are you at calculus?”
This was the opening sentence of Greg Kuperberg’s Facebook status on July 4th, 2016.
“I have a joint paper (on isoperimetric inequalities in differential geometry) in which we need to know that
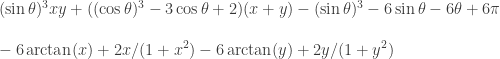
is non-negative for x and y non-negative and  between
between  and
and  . Also, the minimum only occurs for
. Also, the minimum only occurs for  .”
.”
Let’s take a moment to appreciate the complexity of the mathematical statement above. It is a non-linear inequality in three variables, mixing trigonometry with algebra and throwing in some arc-tangents for good measure. Greg, continued:
“We proved it, but only with the aid of symbolic algebra to factor an algebraic variety into irreducible components. The human part of our proof is also not really a cake walk.
A simpler proof would be way cool.”
I was hooked. The cubic terms looked a little intimidating, but if I converted x and y into  and
and 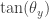 , respectively, as one of the comments on Facebook promptly suggested, I could at least get rid of the annoying arc-tangents and then calculus and trigonometry would take me the rest of the way. Greg replied to my initial comment outlining a quick route to the proof: “Let me just caution that we found the problem unyielding.” Hmm… Then, Greg revealed that the paper containing the original proof was over three years old (had he been thinking about this since then? that’s what true love must be like.) Titled “The Cartan-Hadamard Conjecture and The Little Prince“, the above inequality makes its appearance as Lemma 7.1 on page 45 (of 63). To quote the paper: “Although the lemma is evident from contour plots, the authors found it surprisingly tricky to prove rigorously.”
, respectively, as one of the comments on Facebook promptly suggested, I could at least get rid of the annoying arc-tangents and then calculus and trigonometry would take me the rest of the way. Greg replied to my initial comment outlining a quick route to the proof: “Let me just caution that we found the problem unyielding.” Hmm… Then, Greg revealed that the paper containing the original proof was over three years old (had he been thinking about this since then? that’s what true love must be like.) Titled “The Cartan-Hadamard Conjecture and The Little Prince“, the above inequality makes its appearance as Lemma 7.1 on page 45 (of 63). To quote the paper: “Although the lemma is evident from contour plots, the authors found it surprisingly tricky to prove rigorously.”
As I filled pages of calculations and memorized every trigonometric identity known to man, I realized that Greg was right: the problem was highly intractable. The quick solution that was supposed to take me two to three days turned into two weeks of hell, until I decided to drop the original approach and stick to doing calculus with the known unknowns, x and y. The next week led me to a set of three non-linear equations mixing trigonometric functions with fourth powers of x and y, at which point I thought of giving up. I knew what I needed to do to finish the proof, but it looked freaking insane. Still, like the masochist that I am, I continued calculating away until my brain was mush. And then, yesterday, during a moment of clarity, I decided to go back to one of the three equations and rewrite it in a different way. That is when I noticed the error. I had solved for  in terms of x and y, but I had made a mistake that had cost me 10 days of intense work with no end in sight. Once I found the mistake, the whole proof came together within about an hour. At that moment, I felt a mix of happiness (duh), but also sadness, as if someone I had grown fond of no longer had a reason to spend time with me and, at the same time, I had ran out of made-up reasons to hang out with them. But, yeah, I mostly felt happiness.
in terms of x and y, but I had made a mistake that had cost me 10 days of intense work with no end in sight. Once I found the mistake, the whole proof came together within about an hour. At that moment, I felt a mix of happiness (duh), but also sadness, as if someone I had grown fond of no longer had a reason to spend time with me and, at the same time, I had ran out of made-up reasons to hang out with them. But, yeah, I mostly felt happiness.

Greg Kuperberg pondering about the universe of mathematics.
Before I present the proof below, I want to take a moment to say a few words about Greg, whom I consider to be the John Preskill of mathematics: a lodestar of sanity in a sea of hyperbole (to paraphrase Scott Aaronson). When I started grad school at UC Davis back in 2003, quantum information theory and quantum computing were becoming “a thing” among some of the top universities around the US. So, I went to several of the mathematics faculty in the department asking if there was a course on quantum information theory I could take. The answer was to “read Nielsen and Chuang and then go talk to Professor Kuperberg”. Being a foolish young man, I skipped the first part and went straight to Greg to ask him to teach me (and four other brave souls) quantum “stuff”. Greg obliged with a course on… quantum probability and quantum groups. Not what I had in mind. This guy was hardcore. Needless to say, the five brave souls taking the class (mostly fourth year graduate students and me, the noob) quickly became three, then two gluttons for punishment (the other masochist became one of my best friends in grad school). I could not drop the class, not because I had asked Greg to do this as a favor to me, but because I knew that I was in the presence of greatness (or maybe it was Stockholm syndrome). My goal then, as an aspiring mathematician, became to one day have a conversation with Greg where, for some brief moment, I would not sound stupid. A man of incredible intelligence, Greg is that rare individual whose character matches his intellect. Much like the anti-heroes portrayed by Humphrey Bogart in Casablanca and the Maltese Falcon, Greg keeps a low-profile, seems almost cynical at times, but in the end, he works harder than everyone else to help those in need. For example, on MathOverflow, a question and answer website for professional mathematicians around the world, Greg is listed as one of the top contributors of all time.
But, back to the problem. The past four weeks thinking about it have oscillated between phases of “this is the most fun I’ve had in years!” to “this is Greg’s way of telling me I should drop math and become a go-go dancer”. Now that the ordeal is over, I can confidently say that the problem is anything but “dull” (which is how Greg felt others on MathOverflow would perceive it, so he never posted it there). In fact, if I ever have to teach Calculus, I will subject my students to the step-by-step proof of this problem. OK, here is the proof. This one is for you Greg. Thanks for being such a great role model. Sorry I didn’t get to tell you until now. And you are right not to offer a “bounty” for the solution. The journey (more like, a trip to Mordor and back) was all the money.
The proof: The first thing to note (and if I had read Greg’s paper earlier than today, I would have known as much weeks ago) is that the following equality holds (which can be verified quickly by differentiating both sides):
 .
.
Using the above equality (and the equivalent one for y), we get:

Now comes the fun part. We differentiate with respect to  , x and y, and set to zero to find all the maxima and minima of
, x and y, and set to zero to find all the maxima and minima of  (though we are only interested in the global minimum, which is supposed to be at
(though we are only interested in the global minimum, which is supposed to be at  . Some high-school level calculus yields:
. Some high-school level calculus yields:
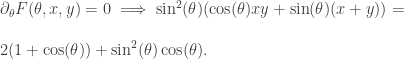
At this point, the most well-known trigonometric identity of all time, 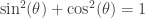 , can be used to show that the right-hand-side can be re-written as:
, can be used to show that the right-hand-side can be re-written as:
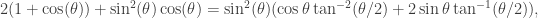
where I used (my now favorite) trigonometric identity:  (note to the reader:
(note to the reader: 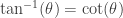 ). Putting it all together, we now have the very suggestive condition:
). Putting it all together, we now have the very suggestive condition:
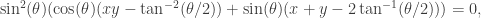
noting that, despite appearances, 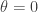 is not a solution (as can be checked from the original form of this equality, unless
is not a solution (as can be checked from the original form of this equality, unless  and
and  are infinite, in which case the expression is clearly non-negative, as we show towards the end of this post). This leaves us with
are infinite, in which case the expression is clearly non-negative, as we show towards the end of this post). This leaves us with 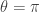 and
and

as candidates for where the minimum may be. A quick check shows that:
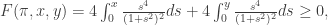
since x and y are non-negative. The following obvious substitution becomes our greatest ally for the rest of the proof:

Substituting the above in the remaining condition for  , and using again that
, and using again that  , we get:
, we get:

which can be further simplified to (if you are paying attention to minus signs and don’t waste a week on a wild-goose chase like I did):
 .
.
As Greg loves to say, we are finally cooking with gas. Note that the expression is symmetric in  and
and  , which should be obvious from the symmetry of
, which should be obvious from the symmetry of  in x and y. That observation will come in handy when we take derivatives with respect to x and y now. Factoring
in x and y. That observation will come in handy when we take derivatives with respect to x and y now. Factoring  , we get:
, we get:
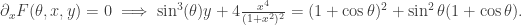
Substituting x and y with  , respectively and using the identities
, respectively and using the identities  and
and  the above expression simplifies significantly to the following expression:
the above expression simplifies significantly to the following expression:
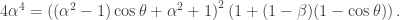
Using  , which we derived earlier by looking at the extrema of
, which we derived earlier by looking at the extrema of  with respect to
with respect to  , and noting that the global minimum would have to be an extremum with respect to all three variables, we get:
, and noting that the global minimum would have to be an extremum with respect to all three variables, we get:
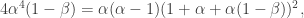
where we used  and
and

We may assume, without loss of generality, that 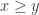 . If
. If 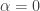 , then
, then 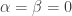 , which leads to the contradiction
, which leads to the contradiction  , unless the other condition,
, unless the other condition, 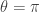 , holds, which leads to
, holds, which leads to 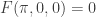 . Dividing through by
. Dividing through by  and re-writing
and re-writing  , yields:
, yields:

which can be further modified to:
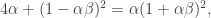
and, similarly for  (due to symmetry):
(due to symmetry):

Subtracting the two equations from each other, we get:
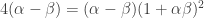 ,
,
which implies that 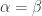 and/or
and/or  . The first leads to
. The first leads to 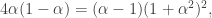 which immediately implies
which immediately implies 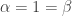 (since the left and right side of the equality have opposite signs otherwise). The second one implies that either
(since the left and right side of the equality have opposite signs otherwise). The second one implies that either 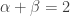 , or
, or  , which follows from the earlier equation
, which follows from the earlier equation 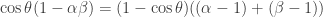 . If
. If 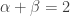 and
and  , it is easy to see that
, it is easy to see that 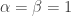 is the only solution by expanding
is the only solution by expanding  . If, on the other hand,
. If, on the other hand,  , then looking at the original form of
, then looking at the original form of  , we see that
, we see that 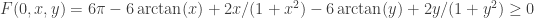 , since
, since 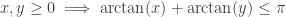 .
.
And that concludes the proof, since the only cases for which all three conditions are met lead to 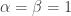 and, hence,
and, hence,  . The minimum of
. The minimum of 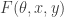 at these values is always zero. That’s right, all this work to end up with “nothing”. But, at least, the last four weeks have been anything but dull.
at these values is always zero. That’s right, all this work to end up with “nothing”. But, at least, the last four weeks have been anything but dull.
Update: Greg offered Lemma 7.4 from the same paper as another challenge (the sines, cosines and tangents are now transformed into hyperbolic trigonometric functions, with a few other changes, mostly in signs, thrown in there). This is a more hardcore-looking inequality, but the proof turns out to follow the steps of Lemma 7.1 almost identically. In particular, all the conditions for extrema are exactly the same, with the only difference being that cosine becomes hyperbolic cosine. It is an awesome exercise in calculus to check this for yourself. Do it. Unless you have something better to do.
. The motivation behind this project was to examine more closely the transformation between a topological insulator and a state exhibiting the anomalous hall effect (AHE).
and numerous other TIs with similar make-up.
exhibit this gap opening due to the surface state of
interacting via the proximity effect with a ferromagnet. Our contention is that a similar material, Cr-doped
, exhibits a similar effect, but more homogeneously because of reduced structural strain between atoms. Specifically, at temperatures below the Curie temperature (Tc), we expect to see a gap in the energy band and an overall increase in the gap magnitude. In short, the main goal of my summer project was to observe the gapping of our TI’s energy band.





















