This is a jubilee year.* In November 1964, John Bell submitted a paper to the obscure (and now defunct) journal Physics. That paper, entitled “On the Einstein Podolsky Rosen Paradox,” changed how we think about quantum physics.
The paper was about quantum entanglement, the characteristic correlations among parts of a quantum system that are profoundly different than correlations in classical systems. Quantum entanglement had first been explicitly discussed in a 1935 paper by Einstein, Podolsky, and Rosen (hence Bell’s title). Later that same year, the essence of entanglement was nicely and succinctly captured by Schrödinger, who said, “the best possible knowledge of a whole does not necessarily include the best possible knowledge of its parts.” Schrödinger meant that even if we have the most complete knowledge Nature will allow about the state of a highly entangled quantum system, we are still powerless to predict what we’ll see if we look at a small part of the full system. Classical systems aren’t like that — if we know everything about the whole system then we know everything about all the parts as well. I think Schrödinger’s statement is still the best way to explain quantum entanglement in a single vigorous sentence.
To Einstein, quantum entanglement was unsettling, indicating that something is missing from our understanding of the quantum world. Bell proposed thinking about quantum entanglement in a different way, not just as something weird and counter-intuitive, but as a resource that might be employed to perform useful tasks. Bell described a game that can be played by two parties, Alice and Bob. It is a cooperative game, meaning that Alice and Bob are both on the same side, trying to help one another win. In the game, Alice and Bob receive inputs from a referee, and they send outputs to the referee, winning if their outputs are correlated in a particular way which depends on the inputs they receive.
But under the rules of the game, Alice and Bob are not allowed to communicate with one another between when they receive their inputs and when they send their outputs, though they are allowed to use correlated classical bits which might have been distributed to them before the game began. For a particular version of Bell’s game, if Alice and Bob play their best possible strategy then they can win the game with a probability of success no higher than 75%, averaged uniformly over the inputs they could receive. This upper bound on the success probability is Bell’s famous inequality.**
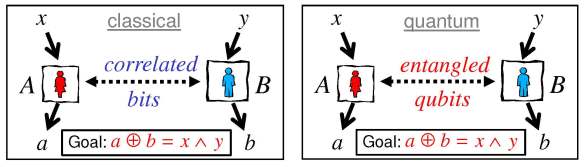
Classical and quantum versions of Bell’s game. If Alice and Bob share entangled qubits rather than classical bits, then they can win the game with a higher success probability.
There is also a quantum version of the game, in which the rules are the same except that Alice and Bob are now permitted to use entangled quantum bits (“qubits”) which were distributed before the game began. By exploiting their shared entanglement, they can play a better quantum strategy and win the game with a higher success probability, better than 85%. Thus quantum entanglement is a useful resource, enabling Alice and Bob to play the game better than if they shared only classical correlations instead of quantum correlations.
And experimental physicists have been playing the game for decades, winning with a success probability that violates Bell’s inequality. The experiments indicate that quantum correlations really are fundamentally different than, and stronger than, classical correlations.
Why is that such a big deal? Bell showed that a quantum system is more than just a probabilistic classical system, which eventually led to the realization (now widely believed though still not rigorously proven) that accurately predicting the behavior of highly entangled quantum systems is beyond the capacity of ordinary digital computers. Therefore physicists are now striving to scale up the weirdness of the microscopic world to larger and larger scales, eagerly seeking new phenomena and unprecedented technological capabilities.
1964 was a good year. Higgs and others described the Higgs mechanism, Gell-Mann and Zweig proposed the quark model, Penzias and Wilson discovered the cosmic microwave background, and I saw the Beatles on the Ed Sullivan show. Those developments continue to reverberate 50 years later. We’re still looking for evidence of new particle physics beyond the standard model, we’re still trying to unravel the large scale structure of the universe, and I still like listening to the Beatles.
Bell’s legacy is that quantum entanglement is becoming an increasingly pervasive theme of contemporary physics, important not just as the source of a quantum computer’s awesome power, but also as a crucial feature of exotic quantum phases of matter, and even as a vital element of the quantum structure of spacetime itself. 21st century physics will advance not only by probing the short-distance frontier of particle physics and the long-distance frontier of cosmology, but also by exploring the entanglement frontier, by elucidating and exploiting the properties of increasingly complex quantum states.
 Sometimes I wonder how the history of physics might have been different if there had been no John Bell. Without Higgs, Brout and Englert and others would have elucidated the spontaneous breakdown of gauge symmetry in 1964. Without Gell-Mann, Zweig could have formulated the quark model. Without Penzias and Wilson, Dicke and collaborators would have discovered the primordial black-body radiation at around the same time.
Sometimes I wonder how the history of physics might have been different if there had been no John Bell. Without Higgs, Brout and Englert and others would have elucidated the spontaneous breakdown of gauge symmetry in 1964. Without Gell-Mann, Zweig could have formulated the quark model. Without Penzias and Wilson, Dicke and collaborators would have discovered the primordial black-body radiation at around the same time.
But it’s not obvious which contemporary of Bell, if any, would have discovered his inequality in Bell’s absence. Not so many good physicists were thinking about quantum entanglement and hidden variables at the time (though David Bohm may have been one notable exception, and his work deeply influenced Bell.) Without Bell, the broader significance of quantum entanglement would have unfolded quite differently and perhaps not until much later. We really owe Bell a great debt.
*I’m stealing the title and opening sentence of this post from Sidney Coleman’s great 1981 lectures on “The magnetic monopole 50 years later.” (I’ve waited a long time for the right opportunity.)
**I’m abusing history somewhat. Bell did not use the language of games, and this particular version of the inequality, which has since been extensively tested in experiments, was derived by Clauser, Horne, Shimony, and Holt in 1969.
