One of the most enjoyable and inspiring physics papers I have read in recent years is this one by Mark Van Raamsdonk. Building on earlier observations by Maldacena and by Ryu and Takayanagi. Van Raamsdonk proposed that quantum entanglement is the fundamental ingredient underlying spacetime geometry.* Since my first encounter with this provocative paper, I have often mused that it might be a Good Thing for someone to take Van Raamsdonk’s idea really seriously.
Now someone has.
I love wormholes. (Who doesn’t?) Picture two balls, one here on earth, the other in the Andromeda galaxy. It’s a long trip from one ball to the other on the background space, but there’s a shortcut:You can walk into the ball on earth and moments later walk out of the ball in Andromeda. That’s a wormhole.
I’ve mentioned before that John Wheeler was one of my heros during my formative years. Back in the 1950s, Wheeler held a passionate belief that “everything is geometry,” and one particularly intriguing idea he called “charge without charge.” There are no pointlike electric charges, Wheeler proclaimed; rather, electric field lines can thread the mouth of a wormhole. What looks to you like an electron is actually a tiny wormhole mouth. If you were small enough, you could dive inside the electron and emerge from a positron far away. In my undergraduate daydreams, I wished this idea could be true.
But later I found out more about wormholes, and learned about “topological censorship.” It turns out that if energy is nonnegative, Einstein’s gravitational field equations prevent you from traversing a wormhole — the throat always pinches off (or becomes infinitely long) before you get to the other side. It has sometimes been suggested that quantum effects might help to hold the throat open (which sounds like a good idea for a movie), but today we’ll assume that wormholes are never traversable no matter what you do.
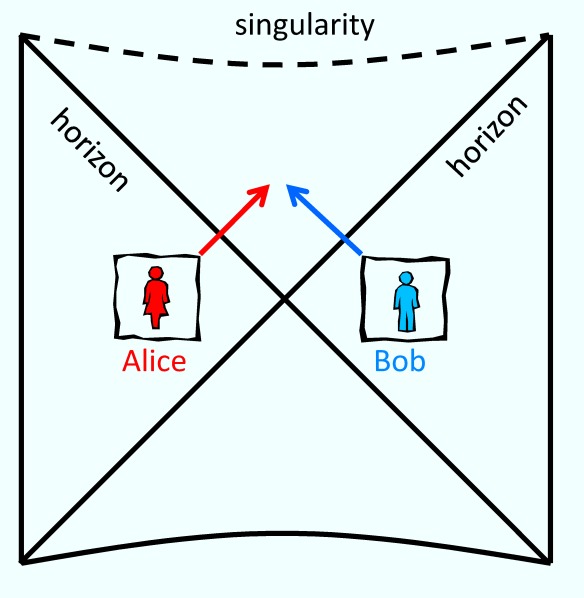
Love in a wormhole throat: Alice and Bob are in different galaxies, but each lives near a black hole, and their black holes are connected by a wormhole. If both jump into their black holes, they can enjoy each other’s company for a while before meeting a tragic end.
Are wormholes any fun if we can never traverse them? The answer might be yes if two black holes are connected by a wormhole. Then Alice on earth and Bob in Andromeda can get together quickly if each jumps into a nearby black hole. For solar mass black holes Alice and Bob will have only 10 microseconds to get acquainted before meeting their doom at the singularity. But if the black holes are big enough, Alice and Bob might have a fulfilling relationship before their tragic end.
This observation is exploited in a recent paper by Juan Maldacena and Lenny Susskind (MS) in which they reconsider the AMPS puzzle (named for Almheiri, Marolf, Polchinski, and Sully). I wrote about this puzzle before, so I won’t go through the whole story again. Here’s the short version: while classical correlations can easily be shared by many parties, quantum correlations are harder to share. If Bob is highly entangled with Alice, that limits his ability to entangle with Carrie, and if he entangles with Carrie instead he can’t entangle with Alice. Hence we say that entanglement is “monogamous.” Now, if, as most of us are inclined to believe, information is “scrambled” but not destroyed by an evaporating black hole, then the radiation emitted by an old black hole today should be highly entangled with radiation emitted a long time ago. And if, as most of us are inclined to believe, nothing unusual happens (at least not right away) to an observer who crosses the event horizon of a black hole, then the radiation emitted today should be highly entangled with stuff that is still inside the black hole. But we can’t have it both ways without violating the monogamy of entanglement!
The AMPS puzzle invites audacious reponses, and AMPS were suitably audacious. They proposed that an old black hole has no interior — a freely falling observer meets her doom right at the horizon rather than at a singularity deep inside.
MS are also audacious, but in a different way. They helpfully summarize their key point succinctly in a simple equation:
ER = EPR
Here, EPR means Einstein-Podolsky-Rosen, whose famous paper highlighted the weirdness of quantum correlations, while ER means Einstein-Rosen (sorry, Podolsky), who discovered wormhole solutions to the Einstein equations. (Both papers were published in 1935.) MS (taking Van Raamsdonk very seriously) propose that whenever any two quantum subsystems are entangled they are connected by a wormhole. In many cases, these wormholes are highly quantum mechanical, but in some cases (where the quantum system under consideration has a weakly coupled “gravitational dual”), the wormhole can have a smooth geometry like the one ER described. That wormholes are not traversable is important for the consistency of ER = EPR: just as Alice cannot use their shared entanglement to send a message to Bob instantaneously, so she is unable to send Bob a message through their shared wormhole.
AMPS imagined that Alice could distill qubit C from the black hole’s early radiation and carry it back to the black hole, successfully verifying its entanglement with another qubit B distilled from the recent radiation. Monogamy then ensures that qubit B cannot be entangled with qubit A behind the horizon. Hence when Alice falls through the horizon she will not observe the quiescent vacuum state in which A and B are entangled; instead she encounters a high-energy particle. MS agree with this conclusion.
AMPS go on to say that Alice’s actions before entering the black hole could not have created that energetic particle; it must have been there all along, one of many such particles constituting a seething firewall.
Here MS disagree. They argue that the excitation encountered by Alice as she crosses the horizon was actually created by Alice herself when she interacted with qubit C. How could Alice’s actions, executed far, far away from the black hole, dramatically affect the state of the black hole’s interior? Because C and A are connected by a wormhole!
The ER = EPR conjecture seems to allow us to view the early radiation with which the black hole is entangled as a complementary description of the black hole interior. It’s not clear yet whether this picture works in detail, and even if it does there could still be firewalls; maybe in some sense the early radiation is connected to the black hole via a wormhole, yet this wormhole is wildly fluctuating rather than a smooth geometry. Still, MS provide a promising new perspective on a deep problem.
As physicists we often rely on our sense of smell in judging scientific ideas, and earlier proposed resolutions of the AMPS puzzle (like firewalls) did not smell right. At first whiff, ER = EPR may smell fresh and sweet, but it will have to ripen on the shelf for a while. If this idea is on the right track, there should be much more to say about it. For now, wormhole lovers can relish the possibilities.
Eventually, Wheeler discarded “everything is geometry” in favor of an ostensibly deeper idea: “everything is information.” It would be a fitting vindication of Wheeler’s vision if everything in the universe, including wormholes, is made of quantum correlations.
*Update: Commenter JM reminded me to mention Brian Swingle’s beautiful 2009 paper, which preceded Van Raamsdonk’s and proposed a far-reaching connection between quantum entanglement and spacetime geometry.

Pingback: Space Emerging from Quantum Mechanics | Sean Carroll
Pingback: Espaço Emergindo da Mecânica Quântica | Universo Racionalista
Gheorghe Rakoczy, better known as
St. Germain, used a Cartesian coordinate system to illustrate what is
“in”, and what is “formless”.
The X axis represents polarities separated. The Y axis represents
polarities united and cancelled out.
At the arch defined by the diameter from the origin, 0, X to Y =
3.14159265… you have flat timespace. Within this arch going in toward
the origin you have timespaces with values less than 3.14159265…
By leaving the rigid (ting) orthogonality (chen) of flat timespace
matter gets more more tenuous, a tenuousity indistinguishable from that
which is called spirit.
Also, along that vector, the mind gets more and more powerful to
materialize its visualizations.
In flat timespace you have to earn what you get.
In, toward the origin a little, a ritual will get you what you want. In
further, a symbol will get you what you want. In still further, just
writing what you want will get it. In further than that, saying what you
want will get it. “If you have the faith of a mustard seed and say to
this mountain move, it shall be moved”. You go to the timeline where the
mountain is elsewhere.
So, you can see that going in along the fifth dimension, defined by Dr.
Lisa Randall, professor of quantum physics at Harvard University,
defined for the gravitational analogue, you get your power by having it
easier to move to the resonant timeline of your ideation, along the
sixth dimension, defined by the quantum physicist, Dr. Hugh Everett.
In a little more and your visualizations will all manifest. And, in
still more, and every thought will manifest as your reality. I don’t
know about you, but, I cannot control all my thoughts. And I can be
pessimistic. I don’t like to use the word “negative”. Many scientific
negatives are very good, and visa versa, many scientific positives are
very bad.
The power of the mind is will times imagination, just as sure as, power
in mechanics is force times velocity, power in electricity is voltage
times current, and power in thermodynamics is temperature times entropy
production rate, EPR.
We get “in” the easiest by EPR. In Dr. Stanislav Grof’s holotropic
breathing sessions (see http://www.holotropic.com ) assistants are
absolutely required to have experienced and safely handled holotropic
breathing themselves.
Why? When a client goes “in” by holotropic breathing, or any other
method of vagal stimulation, he brings all those near him in with him.
This is the secret of sacrifice.
Originally, sacrifice wasn’t giving up something you like. It was more
like “Eight Millimeter”, but, watch your Karma, it’s unethical.
Soviet anthropologists defined this vagal stimulation to be the real
witchcraft. Wiccans doing rituals isn’t real witchcraft.
Soviet anthropologists defined sorcery to be probability manipulations.
Rituals can be sorcery.
If we create our own fast EPR situation it will create the same field as
the person deep into holotropic breathing. EPR is identical with
polarity cancellation rate.
Take a good conductive electrolyte, to allow opposite polarities to
cancel out fast. Salt & vinegar in which copper has been dissolved to
produce a highly conductive copper acetate solution is easiest. A
lantern battery, used as like electroplating set up, will dissolve the
copper fast.
Sex magick. Mix your opposite polarities in the solution. And, it is
absolutely antiseptic. Authoritarians complained that the sex magick as
describes in Frater Achad’s (Stanfield Jone’s) “The Secrets of the
G.’.B.’.G.’.” was a public health hazard.
I haven’t even been able to find anything about the book on the
internet. I bought the book from Llewellyn in 1969. Even that Llewellyn
is gone. Chester-Kent took it over, and Isaac Bonawitz was fired for
publishing my material.
Such a brew is alchemy. It is harmful if taken internally. Bottle it,
and it will work for you, even if you are a thousand miles away from it.
Don’t worry, the polarities wont be used up. The polarities are
continually teleported to the bottle by probability transduction
teleportation.
Once you pass within the pi value of two, all quantumly entangled is
transduced into probability, which ranges from lightspeed to instant at
the origin, the core, the heart. Notice, the 61st Kang Xi radical is
heart, the Cantonese for heart is “sin”.
The 160th radical, which is crime, and criminal, is “sin” in Cantonese.
The name Cain in Hebrew is Qop Yod Nun = 160. The Kang Xi radicals and
the Hebrew kaballah dove tail.
The participants of this mixture (called a “shekina”) are quantumly
entangled with the shekina and with each other. It is said there is a
birth here, the Magickal Child. It is a group spirit, demon in Greek,
whose nature is determined by the thoughts at its conception. Make a
wish.
But, it tends to get more and more powerful as its “polarities”, come
together, and also, its conductivity increases. I have seen the thing
rotate inside by itself, like in the movie “Prince of Darkness”, were
the phenomena was implemented by a big shekina in the basement of a
church. That guy who played the part of Eg Chen in “Big Trouble in
Little China” starred in the movie.
It was also the bluish green liquid that levitated out of the bottle in
“Bram Stoker’s Dracula”. It was also levitating out of that big jar,
dripping up to the ceiling, in “Prince of Darkness” also.
When it reaches that degree you will find it easy to manifest your mind.
The subconscious mind gets the greatest power first. When my shekina
reached that degree, every enemy I ever had was dead in a week. I didn’t
even think of them. My subconscious mind did it.
Monsters from the subconscious mind, called the “id” in “The Forbidden
Planet”. I used to teach my students with videos. I used to fashion my
spirit guides after movie characters. Watch out, they incarnate fallen
angels. When I became a Christian I had them all spiritually washed out
by “deliverence” sessions.
Certainly, the legends of magick lamps with geniis in them were
references to these shekinas. Fire is a fast polarity cancellation rate.
Fire is love. There is no light without polarity cancellation.
The polarities that cancel in light bulbs and candles have been
conspicuously ignored by the “system”, just like there was no blueberry
candy commonly sold before this century.
To discover secrets, take universal sets, compare them, and see what’s
missing. There are so many ways to get in trouble beyond written laws.
Gomory is not written in the Bible. It must be alright.
In the Goetia there are 72 demons. They are real group spirits. Raum is
the group spirit of Nazi Germany. Notice I said is. Watch out he’s still
around. Vassago is the group spirit of the Mafia.
But, Gomory is the only “female” spirit in the Goetia. Stimulating the
vishuddha chakra tends to produce estrogen production. But, a Double Y
is a Double Y.
All Cro Magnon males were found to be Double Y’s. They were called
Anakim by their proclivity to profane the sacred mysteries.
Initiation is Hannaka in Hebrew, related to Qanak, Enoch, and the Anak
in Anakim. Homo Sapien orders of knighthood were able to identify Cro
Magnon men by their proclivities. Now the DNA can be easily read, and
female Cro Magnons are now found.
It has been complained that these writings are too complicated. Just
Google what you don’t understand. There are somethings that are even
censored from Google. And, the technicalities are to prove the facts.
Bent timespace doesn’t cause gravity. Fast velocity does both, but, the velocity can’t exceed the speed of light. Gravity bends timespace globally. It’s analogue in electrical engineering, current, of course, also bends timespace globally, which, due to leaving the rigid orthogonality of flat time space, allows faster polarity cancellation rates, also known as entropy production rates in thermodynamics. Visa versa, a fast polarity cancellation rate, entropy production rate, also bends timespace globally. These facts have been “top secret” to keep the people more controllable. The Philadelphia Experiment used the current analogue to teleport to anywhere, and to anytime, by lowering the pi value of that timespace below 2, and thereby all quantumly entangled were transduced into probability. Such travel is called probability transduction travel. Anyone, with enough privacy, can build a polarity cancellation device, like, for example a photon collider, to promote fast polarity cancellation. By lining up parallel mirrors, mirrored on both sides, and flooding them with light, will facilitate photon collisions. For each pair of collided photons there are differentiated a particle and an antiparticle which swiftly cancel out back into photons. Enough of these polarity cancellations bends timespace globally. Bending timespace below 2, all quantumly entangled is transduced into probability, and thereby will teleport to the place and time to which the traveler is tuned. The Philadelphia Experiment was followed up by experiments at Montauk, NY, and finally moved to, and continued at the Naval base in Nevada. To further facilitate the cancellation of these particles and antiparticles, a magnet keeps them nearby. That magnet is called a “flux capacitor”.
Pingback: GraniDiParole
Pingback: Wormhole Mengurai Paradoks Black Hole – Sainstory
Pingback: Here’s one way to get out of a black hole! | Quantum Frontiers
Pingback: Wormholes Untangle a Black Hole Paradox – The Science Page
I (layman) respectfully request strong Oversight consideration at CERN. I realise your involvement is minimal but your knowledgeable, watchfulness is greatly needed it would seem.
Thank you.
At the conclusion of the June 7, 2013 article was mentioned John Wheeler’s idea that “everything is information”. Wheeler also gave us a description of a black hole: ” It is mass without matter. …. There remains behind only gravitational attraction, the attraction of disembodied mass.”
To be noted is the uncanny similarity of that description and our current understanding of dark matter.
If taken seriously, it might lend potential support to the recent argument that black holes are dark matter.
John Wheeler in 1981 characterized a black hole as “Mass without matter”. (Proceedings of the American Philosophical Society 125: 25-37.)
What could that mean?
Wheeler also described spacetime by saying “Spacetime tells mass how to move; mass tells spacetime how to bend”. Stepping back from Einstein to Newton for a moment, the Third Law states that between two masses, “For every action there is an equal and opposite reaction”.
Applying Newton’s Third Law to Wheeler’s “Mass tells spacetime how to bend”, spacetime must be exerting an equal and opposite action on the mass that bends it. Rephrased simply, spacetime and mass interact gravitationally.
To the best of our knowledge, spacetime is not known to interact electromagnetically, nor in any way other than gravitationally. All of a sudden, we have then a description of spacetime that sounds awfully like that of dark matter.
Hence, Wheeler’s “Mass without matter” description of black holes might be modified to “Mass without visible matter”? In any case, as noted in the comment above on December 20, 2017, there is no shortage of speculation that black holes are dark matter.
More fundamentally, could spacetime, dark matter, and black holes be the same reality, albeit playing different roles (thus carrying different names), other than sharing the same description?
Another reason to revisit the June 7, 2013 article is the recent development of traversible wormholes. The thought is that such wormholes could impact the black hole information paradox.
In ER=EPR, the entanglement between two black holes can be thought of as the black holes measuring each other. No measurement can produce predictable outcomes in the quantum world.
Even if ERs are traversible, the above stipulation means information can only be passed to an unpredictable black hole. Quantum rules forbid “designating” a second black hole as the “predictable” recipient for any sending black hole.
Hawking says the message from a black hole is scrambled. He focuses on the message. The above pays heed to the recipients of messages. In a sense, similar to the message in Hawking radiation, the recipient black holes appear “randomly scrambled”, to the sending black hole.
In both cases, the result is that no reliable information can be faithfully passed through the worm holes. Can the information paradox be considered solved?
KC
I wrote about traversable wormholes here:
Thank you for the reminder.
Apologies for failing to link the April article for everyone’s convenience. That was inadvertent, due in part to distraction by a notion where, stealing your words, readers might “be put off by unfamiliar ideas and terminology”.
It is good that the no-cloning theorem is not violated. On the other hand, if one is serious about black holes being governed by quantum rules, there might be a more basic worry. Namely, a suggestion that quantum reality cannot be our familiar classical physical reality (“nonphysical” lacking proper terminology).
If that fundamental concern is valid, black holes could be devoid of interiors. Even the information they hold might be nonphysical, in the above strict sense.
Short of ready availability, a rather clumsy version of the thought experiment on which the conclusion of non-classical physical quantum reality is based can be found in http://www.preposterousuniverse.com/blog/2017/10/13/mind-blowing-quantum-mechanics/.
The possibility of this nonphysical quantum reality facilitated the linking of black holes and dark matter in the Dec 20 comment.
In turn, that has led to a refinement of what “nonphysical” may mean, in the quest to understand a little more, despite Feynman’s lament, what quantum reality might be, in addition to what it might not be.
KC
Pingback: IS A BLACK HOLE THE LITERAL LAKE OF FIRE THE LOST WHAT WOULD HAPPEN IF YOU FELL IN A BLACK HOLE »
Pingback: IS A BLACK HOLE THE LITERAL LAKE OF FIRE THE LOST WHAT WOULD HAPPEN IF YOU FELL IN A BLACK HOLE – SHOP NIGERIA
Pingback: ‘Espaço de Hilbert’, e os limites da ‘lógica simbólica’ | Questões Cosmológicas