Two weeks ago I attended an exciting workshop at Stanford, organized by the It from Qubit collaboration, which I covered enthusiastically on Twitter. Many of the talks at the workshop provided fodder for possible blog posts, but one in particular especially struck my fancy. In explaining how to recover information that has fallen into a black hole (under just the right conditions), Juan Maldacena offered a new perspective on a problem that has worried me for many years. I am eagerly awaiting Juan’s paper, with Douglas Stanford and Zhenbin Yang, which will provide more details.
My cell-phone photo of Juan Maldacena lecturing at Stanford, 22 March 2017.
Almost 10 years ago I visited the Perimeter Institute to attend a conference, and by chance was assigned an office shared with Patrick Hayden. Patrick was a professor at McGill at that time, but I knew him well from his years at Caltech as a Sherman Fairchild Prize Fellow, and deeply respected him. Our proximity that week ignited a collaboration which turned out to be one of the most satisfying of my career.
To my surprise, Patrick revealed he had been thinking about black holes, a long-time passion of mine but not previously a research interest of his, and that he had already arrived at a startling insight which would be central to the paper we later wrote together. Patrick wondered what would happen if Alice possessed a black hole which happened to be highly entangled with a quantum computer held by Bob. He imagined Alice throwing a qubit into the black hole, after which Bob would collect the black hole’s Hawking radiation and feed it into his quantum computer for processing. Drawing on his knowledge about quantum communication through noisy channels, Patrick argued that Bob would only need to grab a few qubits from the radiation in order to salvage Alice’s qubit successfully by doing an appropriate quantum computation.

Alice tosses a qubit into a black hole, which is entangled with Bob’s quantum computer. Bob grabs some Hawking radiation, then does a quantum computation to decode Alice’s qubit.
This idea got my adrenaline pumping, stirring a vigorous dialogue. Patrick had initially assumed that the subsystem of the black hole ejected in the Hawking radiation had been randomly chosen, but we eventually decided (based on a simple picture of the quantum computation performed by the black hole) that it should take a time scaling like M log M (where M is the black hole mass expressed in Planck units) for Alice’s qubit to get scrambled up with the rest of her black hole. Only after this scrambling time would her qubit leak out in the Hawking radiation. This time is actually shockingly short, about a millisecond for a solar mass black hole. The best previous estimate for how long it would take for Alice’s qubit to emerge (scaling like M3), had been about 1067 years.
This short time scale aroused memories of discussions with Lenny Susskind back in 1993, vividly recreated in Lenny’s engaging book The Black Hole War. Because of the black hole’s peculiar geometry, it seemed conceivable that Bob could distill a copy of Alice’s qubit from the Hawking radiation and then leap into the black hole, joining Alice, who could then toss her copy of the qubit to Bob. It disturbed me that Bob would then hold two perfect copies of Alice’s qubit; I was a quantum information novice at the time, but I knew enough to realize that making a perfect clone of a qubit would violate the rules of quantum mechanics. I proposed to Lenny a possible resolution of this “cloning puzzle”: If Bob has to wait outside the black hole for too long in order to distill Alice’s qubit, then when he finally jumps in it may be too late for Alice’s qubit to catch up to Bob inside the black hole before Bob is destroyed by the powerful gravitational forces inside. Revisiting that scenario, I realized that the scrambling time M log M, though short, was just barely long enough for the story to be self-consistent. It was gratifying that things seemed to fit together so nicely, as though a deep truth were being affirmed.
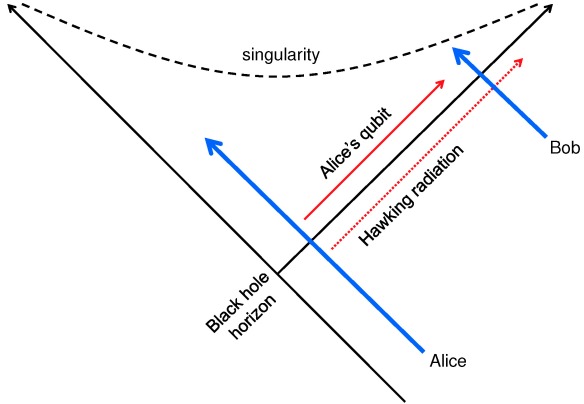
If Bob decodes the Hawking radiation and then jumps into the black hole, can he acquire two identical copies of Alice’s qubit?
Patrick and I viewed our paper as a welcome opportunity to draw the quantum information and quantum gravity communities closer together, and we wrote it with both audiences in mind. We had fun writing it, adding rhetorical flourishes which we hoped would draw in readers who might otherwise be put off by unfamiliar ideas and terminology.
In their recent work, Juan and his collaborators propose a different way to think about the problem. They stripped down our Hawking radiation decoding scenario to a model so simple that it can be analyzed quite explicitly, yielding a pleasing result. What had worried me so much was that there seemed to be two copies of the same qubit, one carried into the black hole by Alice and the other residing outside the black hole in the Hawking radiation. I was alarmed by the prospect of a rendezvous of the two copies. Maldacena et al. argue that my concern was based on a misconception. There is just one copy, either inside the black hole or outside, but not both. In effect, as Bob extracts his copy of the qubit on the outside, he destroys Alice’s copy on the inside!
To reach this conclusion, several ideas are invoked. First, we analyze the problem in the case where we understand quantum gravity best, the case of a negatively curved spacetime called anti-de Sitter space. In effect, this trick allows us to trap a black hole inside a bottle, which is very advantageous because we can study the physics of the black hole by considering what happens on the walls of the bottle. Second, we envision Bob’s quantum computer as another black hole which is entangled with Alice’s black hole. When two black holes in anti-de Sitter space are entangled, the resulting geometry has a “wormhole” which connects together the interiors of the two black holes. Third, we chose the entangled pair of black holes to be in a very special quantum state, called the “thermofield double” state. This just means that the wormhole connecting the black holes is as short as possible. Fourth, to make the analysis even simpler, we suppose there is just one spatial dimension, which makes it easier to draw a picture of the spacetime. Now each wall of the bottle is just a point in space, with the left wall lying outside Bob’s side of the wormhole, and the right wall lying outside Alice’s side.
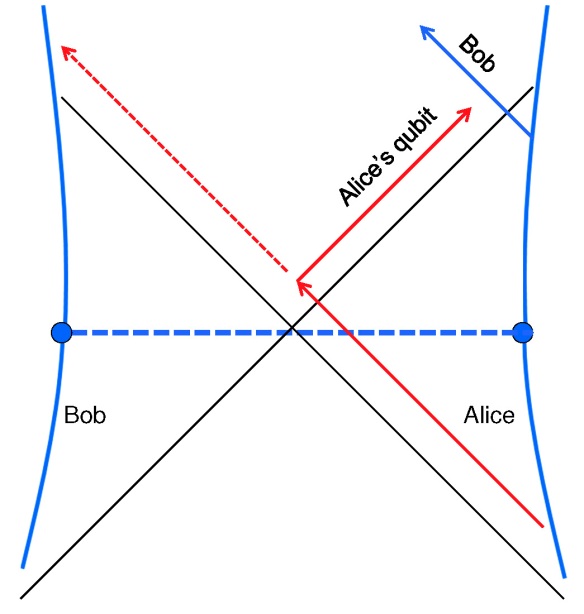
An important property of the wormhole is that it is not traversable. That is, when Alice throws her qubit into her black hole and it enters her end of the wormhole, the qubit cannot emerge from the other end. Instead it is stuck inside, unable to get out on either Alice’s side or Bob’s side. Most ways of manipulating the black holes from the outside would just make the wormhole longer and exacerbate the situation, but in a clever recent paper Ping Gao, Daniel Jafferis, and Aron Wall pointed out an exception. We can imagine a quantum wire connecting the left wall and right wall, which simulates a process in which Bob extracts a small amount of Hawking radiation from the right wall (that is, from Alice’s black hole), and carefully deposits it on the left wall (inserting it into Bob’s quantum computer). Gao, Jafferis, and Wall find that this procedure, by altering the trajectories of Alice’s and Bob’s walls, can actually make the wormhole traversable!

(a) A nontraversable wormhole. Alice’s qubit, thrown into the black hole, never reaches Bob. (b) Stealing some Hawking radiation from Alice’s side and inserting it on Bob’s side makes the wormhole traversable. Now Alice’s qubit reaches Bob, who can easily “decode” it.
This picture gives us a beautiful geometric interpretation of the decoding protocol that Patrick and I had described. It is the interaction between Alice’s wall and Bob’s wall that brings Alice’s qubit within Bob’s grasp. By allowing Alice’s qubit to reach Bob at the other end of the wormhole, that interaction suffices to perform Bob’s decoding task, which is especially easy in this case because Bob’s quantum computer was connected to Alice’s black hole by a short wormhole when she threw her qubit inside.
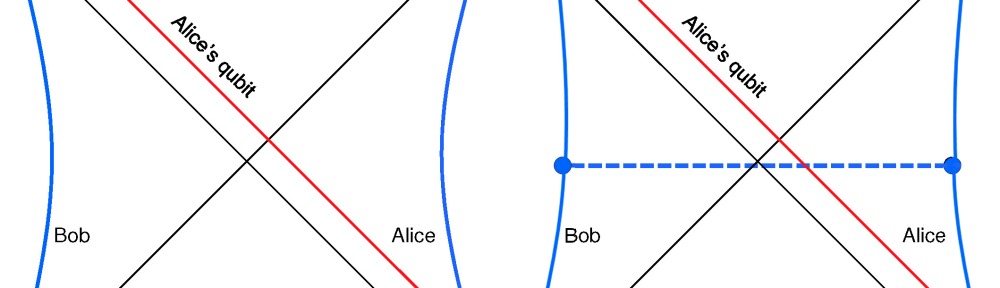
If, after a delay, Bob’s jumps into the black hole, he might find Alice’s qubit inside. But if he does, that qubit cannot be decoded by Bob’s quantum computer. Bob has no way to attain two copies of the qubit.
And what if Bob conducts his daring experiment, in which he decodes Alice’s qubit while still outside the black hole, and then jumps into the black hole to check whether the same qubit is also still inside? The above spacetime diagram contrasts two possible outcomes of Bob’s experiment. After entering the black hole, Alice might throw her qubit toward Bob so he can catch it inside the black hole. But if she does, then the qubit never reaches Bob’s quantum computer, and he won’t be able to decode it from the outside. On the other hand, Alice might allow her qubit to reach Bob’s quantum computer at the other end of the (now traversable) wormhole. But if she does, Bob won’t find the qubit when he enters the black hole. Either way, there is just one copy of the qubit, and no way to clone it. I shouldn’t have been so worried!
Granted, we have only described what happens in an oversimplified model of a black hole, but the lessons learned may be more broadly applicable. The case for broader applicability rests on a highly speculative idea, what Maldacena and Susskind called the ER=EPR conjecture, which I wrote about in this earlier blog post. One consequence of the conjecture is that a black hole highly entangled with a quantum computer is equivalent, after a transformation acting only on the computer, to two black holes connected by a short wormhole (though it might be difficult to actually execute that transformation). The insights of Gao-Jafferis-Wall and Maldacena-Stanford-Yang, together with the ER=EPR viewpoint, indicate that we don’t have to worry about the same quantum information being in two places at once. Quantum mechanics can survive the attack of the clones. Whew!
Thanks to Juan, Douglas, and Lenny for ongoing discussions and correspondence which have helped me to understand their ideas (including a lucid explanation from Douglas at our Caltech group meeting last Wednesday). This story is still unfolding and there will be more to say. These are exciting times!
Really. If a black hole shreds a star over few light years then a human space craft and human beings will Only be spaghetti 1 billion km long. fo
It is amazing to read these stupid theories when we still cannot even land a space craft on Venus with only 95 atmospheric pressures and more or less equal gravity. So multiply that by 1 billion. 1 000 000 000. That’s the number. Of the magnitude of the strength of gravity, pressure and electro magnetic forces around a black hole even approaching it from 1 light year away. A star got ripped apart approaching a black hole from that distance.
So pls be factual.
For about 15 years we have had the ability to do deep space travel LM developed the TR3b Astra.
Excellent.
☺😎😇
The first thought that came to my mind after reading this was ” I wonder if an application could be developed to allow DNA to transfer the black hole”.
Dear John, it’s all very interesting but I find some basic claims of your and Hayden’s paper, and this blog post, puzzling.
After 1/2 of the initial entropy has been radiated via Hawking radiation, isn’t it simply true that a measurement on that radiation is in principle enough to find out – after some quantum calculation etc. – the exact microstate of the remaining, “halved” black hole? So it’s also enough to calculate the probability amplitudes for all subsequent Hawking particles and their correlations.
I don’t see what is the “further information” released by the black hole after the half-point that you talk about.
An important issue is that quantum information isn’t classical information so it always matters what actual measurements one is doing and in which order. At the half-point, Bob can make a complete set of commuting observables on the Hawking radiation, and that will collapse the black hole to some particular pure state from his perspective. But a generic observable to be done later is only predicted probabilistically again, right? It’s because when another observable is measured later, it is probably an observable that doesn’t commute with the previous ones done at the half-point. When that new observable or observables (I find it dumb to talk about qubits because there’s nothing intrinsically binary about the black hole information but I guess you would probably write “qubit” instead of every appearance of “observable”) is measured later, it means a further collapse, and so on.
I surely agree with the natural protection of quantum gravity against quantum clones. When two black holes are entangled, the outcomes of the observations by the two observers inside can be said to agree with one another by “coincidence”, so it doesn’t matter whether we say that it’s a result of the entanglement or whether the degrees of freedom inside are “doubled to start with”.
The point is that the entanglement between the two black holes – i.e. between the “degrees of freedom in their interiors” – is a necessary condition, a pre-existing fact, for both infalling observers to even exist. So they can’t change it. Their relevant Hilbert spaces *are* truncated from two copies to one because causally, they ony have the access – ability to collapse – their one-half of the degrees of freedom (if we imagine them to be doubled at all).
Hi Lubos. In the quantum case, what does it mean to say that Alice throws her qubit into the black hole and Bob later “decodes” it? It means that for any observable M, when Bob measures M his probability distribution of outcomes is the same as Alice would have found if she had measured M instead. (We explain in the paper, but I did not mention in the post, that this statement is not exact; rather, the two probability distributions match to an accuracy which improves exponentially with the number of qubits Bob recovers from the Hawking radiation.)
What seemed surprising when we wrote our paper is that Bob is able to do the decoding after a very short waiting time. You might have thought that Alice’s qubit would stay concealed inside the black hole for a time comparable to the black hole’s evaporation lifetime, but that’s not what happens — it comes out much faster. That’s why we called the paper “Black holes as mirrors”.
Dear John, I am also a bit puzzled by your arguments in the first half of the blog, before talking about Juan’s model. If Alice’s qubit is scrambled up with the black hole and leaks out in the Hawking radiation, from which Bob can extract one qubit information, then doesn’t it mean that Alice’s original qubit has already been destroyed? — in a way that her qubit is now highly entangled with the rest of the black hole and the radiation, such that there is no longer a single pure isolated qubit living there waiting for Bob to compare with his copy of the qubit. Instead, Alice’s qubit would be in a mixed state after the scrambling time?
The problem is to reconcile that expectation with the black hole’s semiclassical causal structure, which seems to indicate that there are two copies of the qubit on the same time slice, one outside the black hole encoded in the Hawking radiation, the other inside the black hole.
Thanks for your answer, Dr. Preskill. Indeed, in the semi-classical picture, Alice’s qubit is safely there in her perspective, and it surely raises up a “cloning paradox” if she can receive Bob’s copy. I’ve sort of jumped out of the semi-classical picture when I thought that Alice’s original qubit must be destroyed after the scrambling time scale.
If Juan’s model problem shows that the underlying quantum dynamics indeed destroy the original qubit, that would make perfect sense.
Dear John, thanks for that answer. Concerning your definition of “decoding”, it may sound problem-free but it’s not.
You may invent a quantum algorithm that is applied to the Hawking radiation and isolates a qubit with the same probability amplitudes as a qubit that an observer inside the black hole may get, assuming the same initial wave function before the black hole is formed.
But that doesn’t mean that the two results – inside and outside (on the quantum computer) – are in any sense equal. The infalling observer has probably made other measurements before this one (but already while inside), and they collapsed her wave function in various ways. But these previous collapses (that already occurred inside) did *not* affect the wave function that the outside observer with the quantum computer should be using.
So the wave functions and the probabilities are unavoidably different whatever you do. Do you disagree? I tried to maximally use the framework of your comment to get back to my point and it seems that we’re back there – I did so because I think that you didn’t really address the beef of my comment. In particular, my comment wasn’t a question about the definition of decoding or anything else.
And when you’re outside, you can’t really emulate the precise sequence of measurements that the observer inside was doing because up to the consistency and required decoherence etc., they were up to her. These choices – the Heisenberg choices – reflected her free will which must be considered independent of the free will of any observer outside.
Dear Lubos, while I know that you are a big defender of the Copenhagen interpretation I must agree with the comments made long ago by Murray Gell-Mann that physicists should strive to reformulate QM problems in a way that does not appeal to observers or free wills. I fully appreciate that by free will you must mean a wholly independent physical process but the language is definitely getting in the way of a crisp understanding of the situation. Surely a free will can decide many things including coordinating based on preconceived protocols so it is unclear what either of you are claiming here.
Dear Ignacio, what came out from Gell-Mann’s approach is really the consistent histories approach (he is one of the co-fathers of it) which is, up to cosmetic changes of the wording, equivalent to the Copenhagen interpretation – and I approve it as a way to state all these things. In that formulation, one needs someone to decide what is the set of alternative histories that may be distinguished. The choice must satisfy some conditions but it is not unique – just like it’s not unique to pick which observable should be observed by an observer. It’s really the same thing as the free will in the Heisenberg choice to choose the observables that are measured – basically just the same applied at all the moments at once.
But my comment doesn’t depend on any “philosophical” aspects of quantum mechanics. No important, quantitative, well-defined question in quantum mechanical theories does. Only people who are wrong and/or vague and sloppy are hiding behind ludicrous claims that “it’s up to the interpretation”. It can never be so. Quantum mechanics is ultimately a well-defined theory and the prescriptions to use it are known, leaving no room for “tangibly” different interpretations. This issue is entirely technical, too. Of course I can reformulate it without any reference to observers or free will. The claim that the events inside and outside (on quantum computer) won’t really be the same is basically equivalent to the statement that observables inside and outside cannot decohere simultaneously. The two “preferred bases” as derived from decoherence are different if we compute them from interactions with the environment inside the black hole; or those with the environment outside. And there’s no decoherence that would make both of them diagonalized.
The free will itself may be given a completely meaningful sense in the context of basic tests and properties of quantum mechanics. And John Conway and Simon Kochen have proven several versions of the free-will theorem, a version of no-go theorem against hidden variables that implies that the random numbers coming from the measurements are really calculated locally and particles etc. therefore have free will, too. The phrase may sound as an unscientific one but within the appropriate context, it is also given a completely meaningful content.
At any rate, comments like yours are being emitted by people who still have serious psychological problems with the basics of quantum mechanics. I guess that John doesn’t really belong to this category, it would make his thinking about quantum computers and quantum gravity impossible.
Dear Lubos you have no idea what I believe or don’t believe beyond what I said in my post. I have no problem at all with QM because I don’t believe it contains inconsistencies. My problem is with your language which plainly obscures the subject. Of course Gell-Mann developed the sum over histories and also advocated changing the language to avoid conveying unintended meanings. It’s online. Search it.
Ignacio, on the contrary, the language or its synonym is absolutely vital to *clarify* all the issues – the language is referring to all the important principles that changed when classical physics was superseded by quantum mechanics. One either misunderstands or obscures quantum mechanics if he tries to *avoid* the language.
I haven’t experienced any “unintended” consequences of my – or Heisenberg’s and Bohr’s etc. – language on the foundations of quantum mechanics. I assure you that the things you vaguely sketched to were fully intended and they are paramount.
Lubos, the puzzle I referred to arises because two copies of Alice’s qubit are both available on the same time slice, but there is more to it than that.
One point you are making, I think, is that there is no sharp paradox if the two copies remain isolated from one another (one inside the black hole and one outside). I agree. To have an operationally meaningful violation of the no-cloning principle, there should be a “referee” who can verify that the cloning has occurred. That’s why I considered the scenario in which Bob extracts one copy of the qubit from outside the black hole, and then sends that copy into the black hole to unite it with the other copy which is already inside. (I left it unsaid that Bob could then do further measurements to verify the cloning. To make the verification statistically convincing, he should actually clone many qubits, and perform measurements on each of the cloned pairs. See below.)
When Hayden and I considered this scenario, we concluded that the verification of the cloning could not be carried out within the domain of applicability of semiclassical approximations. But in their recent work, Maldacena, Stanford, and Yang go further, because they have better control (based on AdS/CFT) of the relevant quantum gravity effects.
As a matter of principle there are a variety of ways to do the cloning test. Suppose I present you with a black box, which I claim is a cloning machine. You insert an input qubit and two output qubits pop out. Are the two output qubits really two copies of the input qubit?
To test this assertion, you use the machine many times in succession (or if you have many identical machines, you can conduct the test many times in parallel). You prepare many input qubits, deciding in each case to prepare an eigenstate with eigenvalue +1 of either sigma_x or sigma_z (two anticommuting Pauli matrices). You keep a record of how the qubit was prepared in each case, but you ensure this record concealed from the machine.
After the machine maps each input qubit to two output qubits, you consult your record; then you measure sigma_x for both copies if the input had been a sigma_x eigenstate, and you measure sigma_z for both copies if the input had been a sigma_z eigenstate. If the cloning had been successful, you would find the measurement outcome +1 for every measurement.
Note that this test is different than verifying entanglement. If the machine produced an entangled state of the two output qubits (which is allowed by quantum mechanics), then neither output qubit would be in an eigenstate of sigma_x (or sigma_z).
In the black hole story, Alice and Bob can cooperate to conduct the test. Here is one way. Alice produces the record specifying how each of n qubits were prepared outside the black hole, and shares this record with Bob. Alice carries all the qubits into the black hole and measures them, checking that the results are what she expected. When Bob extracts the n qubits from the Hawking radiation, he throws them into the black hole and Alice again measures each qubit in the basis specified by her record to complete the cloning verification test.
What we are trying to understand is why this test will not succeed. Hayden and I said that, because Bob has to wait for a while before he can decode the Hawking radiation, his qubits will hit the singularity before Alice can catch up with them. Maldacena et al. explain in greater detail why it is not possible to measure both copies.
Thank for the lucid explanation. Can you elaborate a little more on the connection with this new work by Jafferis and his student? Does the new work by Maldacena allow for traversable wormholes? I thought Maldacena always stressed the point that wormholes are not traversable. Beyond the difficulties of maintaining a negative energy wormhole is there some other discrepancy between the two camps? Or are there two camps?
I’m not sure what new work you are referring to, but as far as I know there is only one camp. Gao, Jafferis, and Wall pointed out that an interaction coupling the two boundaries can make the wormhole traversable. Maldacena, Stanford, and Yang agree.
Dear John, thanks for your services. It’s sort of possible to follow the way how you think about these cloning experiments – and the basic questions are obviously the same for anyone who thinks about these matters – but I don’t know why you try to follow this logic. I hope to clarify what I find illogical.
There is no clear “theoretical framework” in which you try to discuss these matters – because your framework seems to be “mostly” quantum mechanics but not quite because you seem to allow it to be generalized it in some way and you don’t specify the rules of the generalizations or what you’re willing to sacrifice.
Just two examples. One is trivial or perhaps terminological. You say that there’s no sharp paradox because there’s no “referee” who can see the clones. Great that you understand me. I just don’t understand why you call him a “referee” which seems to be a new, and therefore potentially ill-defined, term. As far as I can see, the “referee” should be replaced with the ordinary “observer”. This term “observer” is exactly what it always meant in quantum mechanics and why it was introduced in the mid 1920s at all.
As long as observers – their manipulation with the information – are constrained by the causal diagrams of the spacetime they inhabit, there is no observer who can see both the complete radiation of the black hole – as well as something in the interior. That’s why there can’t be a paradox from the would-be cloning.
You know, my problem is that you don’t make it clear whether you assume the postulates of quantum mechanics and which ones, or whether you try to be phenomenological and allow some non-quantum theories. Your wording doesn’t quite agree with either possibility.
Second, you talk about measurements of sigma_x followed by sigma_z, and talk about a “cloning successful” scenario where both are guaranteed to end up with +1. I don’t understand why you’re discussing such a “possibility” at all. When a spin is observer as sigma_x = +1, then the local laws of QM and basics mathematics of the spin guarantee that the measurement of sigma_z has 50:50 chances of being +1 and –1, right? So the “possibility” you discuss isn’t really possible as long as you respect the postulates of QM, and as long as the low-energy physics – of the spin in a region – is obeyed.
Such paradoxical results may be possible in some non-quantum theory but I would like to see a sketch what such a theory could look like, otherwise you are talking about isolated and theoretical incoherent “episodes from someone’s life”, not something that may be studied by physics which always requires some theoretical framework.
So one can talk about the question whether 1) the postulates of quantum mechanics are obeyed, 2) whether the usual laws of e.g. effective field theory are obeyed in a region, up to some precision. Now, I would just always assume both assumptions. It makes no sense not to assume them because 1) there is no known conceivable framework that could share successes of QM, but wasn’t following its rules, 2) laws of effective QFTs etc. seem experimentally verified. So why don’t you just assume these two things? If you do, then the guaranteed sigma_z=+1 following sigma_x=+1 is obviously impossible, just like it’s generally possible for the linear evolution operator to be quadratic or bilinear.
Even if you assume them, there is a possibility that all the measurable operators may be defined as acting on an appropriate Hilbert space but many degrees of freedom “look” doubled at a spacelike slice. The tasks really reduce to the task how to embed the local field operators into a Hilbert space of some predetermined size so that the postulates of QM hold exactly and the dynamical laws of effective QFT hold approximately and very well. And it may be done especially because the Hilbert space of black hole microstates has an exponentially large dimension. This is really a sensible approach, not just mine etc. Raju, Papadodimas, and surely many others, approach the thing in the same way.
In your paradox-thirsty approach, it looks like in every other sentence, you want to assume something that obviously cannot be true. I don’t know what’s the purpose of this game, except for fooling yourself into thinking that quantum gravity really is plagued by logical paradox – but it demonstrably isn’t.
The literal cloning may only be “demonstrated” if you assume the locality of the effective QFT to be exactly true. It doesn’t have to be exactly true, so the Hilbert space for 2 regions doesn’t contain the simple tensor product but may be and almost certainly is smaller. But the locality may still hold with a huge precision – up to experiments testing a rather large number of things rather precisely.
21.06: Eller ignorera som i fallet med stridsfordon där man frÃ¥n FM konstaterar att trenden med lätta stridsfordon är bruten. Vi är Ã¥ter tillbaka pÃ¥ det som diskuterades i förra inlägget – ansvar. Det blÃ¥ser pÃ¥ toppen. Lyssna pÃ¥ ekots kvällssändning där GD FM och FMV kastar pajer pÃ¥ varandra tillsammans med fÃrstvarsminirse¶n.J K: Vad tror du om "inom ram"…?
Lubos, In the cloning test I described, one does not measure sigma_z following a measurement of sigma_x on the same qubit. Rather, when testing two putative clones of an input qubit, one either measures sigma_x on both or measures sigma_z on both. I was just trying to clarify what I mean by a test to verify cloning. The reason I described the test is that when one encounters an apparent paradox, it’s important to check that the paradox really has a clear operational meaning. I think you agree with that.
Though I don’t consider myself to be “paradox-thirsty” I do think that paradoxes can be useful for helping us to sharpen our thinking.
You and I share the goal of preserving the successes of local effective field theory, while reconciling those successes with the phenomena in quantum gravity for which local effective field theory is not the whole story. Understanding how cloning is avoided in the case of an evaporating black hole is part of that program.
Dear John, indeed, it’s very important to say accurately how the test of the proposed paradox is carried if one wants to claim that there is one.
When one is guaranteed to get sigma_z=+1 on a spin, he can’t be simultaneously guaranteed to get sigma_x=+1 on the same spin (even if you only make one of the two measurements), and he can’t be guaranteed a perfect correlation (or perfect anticorrelation) of sigma_x with another spin, either.
This is easily shown using the mathematics of 2D or 4D Hilbert spaces and you know it very well. “Guaranteed sigma_z=+1” means that the state is an eigenstate of sigma_z with the positive eigenvalue. Because sigma_z,sigma_x don’t commute, the state cannot be an eigenstate of sigma_x. Also, because sigma_z=+1 determines the state of one spin completely (up an an overall complex normalization), the state of a 2-part system can’t be entangled.
Trying to convince oneself that you get results that contradict these basic facts of quantum mechanics isn’t sharpening one’s thinking. It is numbing his thinking. People are sometimes numbing their thinking in order to be led astray. For example, Joe Polchinski has similarly convinced himself that there is really a paradox in order to “sacrifice” something in a big way – in his case, the very existence of the event horizon.
But there is no paradox and therefore there is no reason to sacrifice (or a justification for sacrificing) anything (e.g. the event horizon) in a big way. The same degrees of freedom may be read as some information about the black hole microstate and, by observers inside, about their observations; or as detailed information about the Hawking radiation. These are two or three bases on the same Hilbert space, two or three choices of interesting observables on it.
Imagine that all the degrees of freedom that may be observed are visualized as being in a part of a spaceship. There is a switch in the spaceship that basically changes the time-dependent Hamiltonian. The switch is doing “inside/outside” black hole. OK, so if the switch is set to “inside”, the apparatuses inside the spaceship are arranged so that they measure the “interior fields” of the black hole. When the switch is set to “out”, they arrange to measure some complicated correlations between the Hawking particles – the same quantum information – instead. There’s clearly no cloning, just two different systems to measure something about the information in the spaceship. When an observer makes a measurement with the switch on “inside”, it will clearly affect the subsequent measurements as well, and vice versa. One can’t simultaneously measure both without the disturbance.
This is morally equivalent to the situation of the information inside the black hole and the radiation. The only *counterintuitive* thing is that the fields inside and outside the black hole look totally independent because they’re spacelike separated. But that perfect separation is only valid in some low-energy approximation. When all the detailed short-distance information is maximally taken into account, one discovers that the operators inside and outside don’t quite commute with each other.
Every system of ideas where it is assumed that the vanishing of the commutator – the mutual locality – is perfect is simply wrong and it is unsuprising that when this is taken as an assumption, one may prove *anything*, just like when you assume 1+1=3. That’s exactly how Joe et al. “proved” that there is a firewall on the surface of each black hole that prevents anyone from experiencing anything inside. Anything – including this self-evidently wrong statement – may be proven if one makes a sharply invalid assumption. Such big proven conclusions are not sharp. They are just rudimentary games and random examples of a “liar” in some children’s logical games.
In quantum gravity and even in any quantum mechanics, the question isn’t *whether* two generic observables commute – they almost never do – but what the commutator is and how all these algebras behave. I think that for many years if not decades, quantum gravity has been actually solving this question. I don’t think that it’s in the stage of impressing itself with the cloning paradox anymore – how wonderfully illogical it would be if the quantum information could be cloned. It can’t be cloned and despite that mundane conclusion, one doesn’t need to sacrifice any common-sense predictions of GR or low-energy effective QFT. All the new effects that enter and guarantee the absence of paradoxes are only visible if one has a basically unlimited capability to measure the microstate and/or correlations of the Hawking particles.
Lubos, I think you and I are pretty well aligned in our thinking about the interior of a black hole. I agree that it cannot be precisely correct to regard the inside and outside of a black hole as two subsystems such that observables acting on the interior commute with those acting on the exterior. I would like to understand better the correct way to think about how the interior and exterior are related. I like the recent work of Maldacena, Stanford, and Yang because I feel that it illuminates the issue.
Dear Lubos. You make clearer points below. Nevertheless you, like the people you accuse in your own blog, have an inconsistency in your language. You put down philosophical debates but at the same time you insist that you are quite certain that there is no “objective reality”. Mermin likewise insists that this must be inconsistent with quantum mechanics. In pursuing this point of view you castigate alternative statements with the zeal of Torquemada, while simultaneously accusing those who like to think of alternative constructions of “anti-quantum zeal”. You go so far as to state that different interpretations of quantum mechanics are a total waste of time. This is truly a bold statement. It would be pretty much the only time in the history of science in which a scientific theory can be regarded as final. Yet that is the view you vehemently spouse. Which is not to say that Everett’s work contributes significantly to advance the field but that almost certainly future generations will gain a deeper understanding of this theory. It does remain troubling that one must consider observers outside of the universe to perform observations of the universe. Wishing to find an alternative interpretation for QM is simply natural, though I would agree that so far there hasn’t been much progress in that direction.
I would add one final thought for you. Have considered that Polchinski in advancing what may well be an erroneous notion about firewalls has made more of a contribution to this subject that you have while launching a thousand attacks at anyone who wants to revisit the subject?
That said it is true that I read your blog and have learned a great deal from its contents. But to my mind you CLEARLY go too far.
With every little thing which seems to be building throughout this subject matter, all your perspectives are generally quite refreshing. Neevltheress, I beg your pardon, because I can not subscribe to your entire idea, all be it exciting none the less. It appears to everybody that your comments are generally not entirely justified and in simple fact you are your self not even completely certain of your point. In any event I did take pleasure in reading through it.
Oh my gosh, I think that you’ve solved a problem that my son asked me about something like two years ago!
https://www.youtube.com/edit?o=U&video_id=8Gd1q9tUwfU
In regard to Scott J Robertson’s recent (and oft-cited) Journal of Physics B article “The theory of Hawking radiation in laboratory analogues” (arXiv:1508.02569), which QIP-focussed gedanken experiments involving black holes (if any), are outside the scope of the (perhaps simpler?) theoretical context of QED laboratory analogues?
Here is the student-friendly “rhetorical flourish” that concludes Robertson’s article (hopefully the WordPress spam-filter will allow these paragraphs through):
—————
Despite some tantalizing experimental results — the realization of an analogue black hole in BEC, the detection of a signal from laser pulse filaments in nonlinear optical media, and the observation of the classical stimulated Hawking effect for surface water waves — Hawking radiation remains stubbornly in the realms of theory.
But the idea of its experimental realization is flourishing. Its concepts are constantly being applied to newer analogue systems. The goal is no longer a deeper understanding of gravity — and perhaps, given the surprising emergence of the “horizonless” regime, not so much about general black or white holes either.
Instead, we are aiming to paint a picture of the quantum vacuum — of the content of nothing, of physics at its most fundamental.
—————
To borrow a rhetorical flourish from Feynman’s “Simulating physics with computers” (1982), one lesson of Robertson’s survey is that researchers (young ones especially) can fruitfully “entertain [themselves] by squeezing the difficulty of quantum mechanics into a smaller and smaller place” … that smaller place being QED in the Galilean limit (e.g., liquid helium and/or BECs in classical electromagnetic fields).
Whoever edits and puhsilbes these articles really knows what they’re doing.
there are no “walls” in quantum mechanics
That “there are no ‘walls’ in quantum mechanics” is a (Bohr-style) Great Truth, which is to say, a truth whose opposite is also a Great Truth.
When we examine in detail any real-world device whose performance is optimized to approach quantum limits — that is, any quantum-limited device comprised of atoms interacting electromagnetically — we find diverse walls that are carefully engineered to variously:
* reflect photons (coated mirrors)
* confine photons (single-mode fibers)
* emit photons (lasers)
* detect photons (photodiodes)
* emit phonons (piezoemitters)
* detect phonons (tuned RF cavities)
* confine electrons (metals)
* confine condensates (superconductors)
* confine ions (BEC traps and electrodes)
None of these QED technologies work perfectly, and indeed there are fundamental reasons why QED technologies can no more work perfectly, than a finite-size black holes can cease to emit Hawking radiation.
Indeed there is no predicted quantum phenomenon associated to black holes (known to me), that lacks an illuminating analog in QED devices.
PS An illuminating (literally!) QED example is described by Evans et al. “Observation of Parametric Instability in Advanced LIGO” (arXiv:1502.06058), whose concluding acknoledgment is:
—–
The authors would like to acknowledge the extensive theoretical analysis of parametric instabilities by our Moscow State University colleagues Vladimir Braginsky, Sergey Strigin, and Sergey Vyatchanin, without which these instabilities would have come as a terrible surprise.
—–
Here the phrase “terrible surprise” is a rhetorical flourish reminds that “terrible surprises” all-too-commonly go hand-in-hand with “awesome achievements” … like the awesome achievement of Advanced LIGO’s second observational run (“O2”), which concludes this month! 🙂
In summary, we all share reasons to hope that sustained, scrupulously respectful attention to the diverse quantum mysteries that black holes and QED technologies alike convey to us — including truths that we may experience as “terrible surprises” — will continue to yield “awesome achievements” such as the dawning era of gravitational wave astronomy.
Pingback: Reading List (Apr 9, 2017) | Bespoke Quantitative Solutions
I thought string theory replaced black holes with fuzzballs.
No singularity, no event horizon (in the usual sense).
So in what context are we talking about all this?
Hi John, I tried replying to your comment on Lubos Motl’s blogpost in which he criticises your interpretation of quantum mechanics. However it seems Lubos prohibited my comment from appearing. Here it is anyway:
Hi John,Your support for Everett interpretation is similar to Sidney Coleman. Coleman supports it in his lecture ‘Quantum Mechanics in Your Face’ and you mention his work in your old quantum info notes. But do you then actually believe the universe splits upon every measurement and that the wave function is a real entity instead of a measure of our ignorance? And Lubos, don’t you agree with Coleman’s interpretation in one of your previous posts?
Any comments, John? I’m interested in your current view of Everett interpretation.
And Lubos you may clarify your stance as well w.r.t. Coleman.
Thanks.
The vacuum immediately outside of a black-hole is teeming with high energy Hawking Radiation. I’d assume every single time, the q-bit decoheres well before it gets deep enough for its info to become a hologram on the way out. For an artificial worm-hole you can maybe shed (much of) the Hawking Radiation and such a communications system might form the balance of power (against robots/AI/insanity/evil) beyond 5 or so light years.
Pingback: Guest Post: Nicole Yunger Halpern on What Makes Extraordinary Science Extraordinary | Sean Carroll