Two weeks ago I attended an exciting workshop at Stanford, organized by the It from Qubit collaboration, which I covered enthusiastically on Twitter. Many of the talks at the workshop provided fodder for possible blog posts, but one in particular especially struck my fancy. In explaining how to recover information that has fallen into a black hole (under just the right conditions), Juan Maldacena offered a new perspective on a problem that has worried me for many years. I am eagerly awaiting Juan’s paper, with Douglas Stanford and Zhenbin Yang, which will provide more details.
My cell-phone photo of Juan Maldacena lecturing at Stanford, 22 March 2017.
Almost 10 years ago I visited the Perimeter Institute to attend a conference, and by chance was assigned an office shared with Patrick Hayden. Patrick was a professor at McGill at that time, but I knew him well from his years at Caltech as a Sherman Fairchild Prize Fellow, and deeply respected him. Our proximity that week ignited a collaboration which turned out to be one of the most satisfying of my career.
To my surprise, Patrick revealed he had been thinking about black holes, a long-time passion of mine but not previously a research interest of his, and that he had already arrived at a startling insight which would be central to the paper we later wrote together. Patrick wondered what would happen if Alice possessed a black hole which happened to be highly entangled with a quantum computer held by Bob. He imagined Alice throwing a qubit into the black hole, after which Bob would collect the black hole’s Hawking radiation and feed it into his quantum computer for processing. Drawing on his knowledge about quantum communication through noisy channels, Patrick argued that Bob would only need to grab a few qubits from the radiation in order to salvage Alice’s qubit successfully by doing an appropriate quantum computation.

Alice tosses a qubit into a black hole, which is entangled with Bob’s quantum computer. Bob grabs some Hawking radiation, then does a quantum computation to decode Alice’s qubit.
This idea got my adrenaline pumping, stirring a vigorous dialogue. Patrick had initially assumed that the subsystem of the black hole ejected in the Hawking radiation had been randomly chosen, but we eventually decided (based on a simple picture of the quantum computation performed by the black hole) that it should take a time scaling like M log M (where M is the black hole mass expressed in Planck units) for Alice’s qubit to get scrambled up with the rest of her black hole. Only after this scrambling time would her qubit leak out in the Hawking radiation. This time is actually shockingly short, about a millisecond for a solar mass black hole. The best previous estimate for how long it would take for Alice’s qubit to emerge (scaling like M3), had been about 1067 years.
This short time scale aroused memories of discussions with Lenny Susskind back in 1993, vividly recreated in Lenny’s engaging book The Black Hole War. Because of the black hole’s peculiar geometry, it seemed conceivable that Bob could distill a copy of Alice’s qubit from the Hawking radiation and then leap into the black hole, joining Alice, who could then toss her copy of the qubit to Bob. It disturbed me that Bob would then hold two perfect copies of Alice’s qubit; I was a quantum information novice at the time, but I knew enough to realize that making a perfect clone of a qubit would violate the rules of quantum mechanics. I proposed to Lenny a possible resolution of this “cloning puzzle”: If Bob has to wait outside the black hole for too long in order to distill Alice’s qubit, then when he finally jumps in it may be too late for Alice’s qubit to catch up to Bob inside the black hole before Bob is destroyed by the powerful gravitational forces inside. Revisiting that scenario, I realized that the scrambling time M log M, though short, was just barely long enough for the story to be self-consistent. It was gratifying that things seemed to fit together so nicely, as though a deep truth were being affirmed.
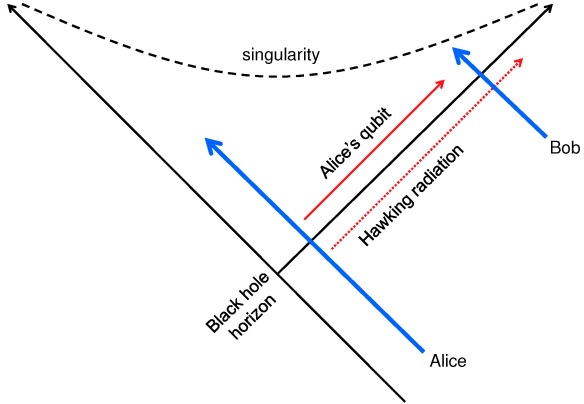
If Bob decodes the Hawking radiation and then jumps into the black hole, can he acquire two identical copies of Alice’s qubit?
Patrick and I viewed our paper as a welcome opportunity to draw the quantum information and quantum gravity communities closer together, and we wrote it with both audiences in mind. We had fun writing it, adding rhetorical flourishes which we hoped would draw in readers who might otherwise be put off by unfamiliar ideas and terminology.
In their recent work, Juan and his collaborators propose a different way to think about the problem. They stripped down our Hawking radiation decoding scenario to a model so simple that it can be analyzed quite explicitly, yielding a pleasing result. What had worried me so much was that there seemed to be two copies of the same qubit, one carried into the black hole by Alice and the other residing outside the black hole in the Hawking radiation. I was alarmed by the prospect of a rendezvous of the two copies. Maldacena et al. argue that my concern was based on a misconception. There is just one copy, either inside the black hole or outside, but not both. In effect, as Bob extracts his copy of the qubit on the outside, he destroys Alice’s copy on the inside!
To reach this conclusion, several ideas are invoked. First, we analyze the problem in the case where we understand quantum gravity best, the case of a negatively curved spacetime called anti-de Sitter space. In effect, this trick allows us to trap a black hole inside a bottle, which is very advantageous because we can study the physics of the black hole by considering what happens on the walls of the bottle. Second, we envision Bob’s quantum computer as another black hole which is entangled with Alice’s black hole. When two black holes in anti-de Sitter space are entangled, the resulting geometry has a “wormhole” which connects together the interiors of the two black holes. Third, we chose the entangled pair of black holes to be in a very special quantum state, called the “thermofield double” state. This just means that the wormhole connecting the black holes is as short as possible. Fourth, to make the analysis even simpler, we suppose there is just one spatial dimension, which makes it easier to draw a picture of the spacetime. Now each wall of the bottle is just a point in space, with the left wall lying outside Bob’s side of the wormhole, and the right wall lying outside Alice’s side.
An important property of the wormhole is that it is not traversable. That is, when Alice throws her qubit into her black hole and it enters her end of the wormhole, the qubit cannot emerge from the other end. Instead it is stuck inside, unable to get out on either Alice’s side or Bob’s side. Most ways of manipulating the black holes from the outside would just make the wormhole longer and exacerbate the situation, but in a clever recent paper Ping Gao, Daniel Jafferis, and Aron Wall pointed out an exception. We can imagine a quantum wire connecting the left wall and right wall, which simulates a process in which Bob extracts a small amount of Hawking radiation from the right wall (that is, from Alice’s black hole), and carefully deposits it on the left wall (inserting it into Bob’s quantum computer). Gao, Jafferis, and Wall find that this procedure, by altering the trajectories of Alice’s and Bob’s walls, can actually make the wormhole traversable!

(a) A nontraversable wormhole. Alice’s qubit, thrown into the black hole, never reaches Bob. (b) Stealing some Hawking radiation from Alice’s side and inserting it on Bob’s side makes the wormhole traversable. Now Alice’s qubit reaches Bob, who can easily “decode” it.
This picture gives us a beautiful geometric interpretation of the decoding protocol that Patrick and I had described. It is the interaction between Alice’s wall and Bob’s wall that brings Alice’s qubit within Bob’s grasp. By allowing Alice’s qubit to reach Bob at the other end of the wormhole, that interaction suffices to perform Bob’s decoding task, which is especially easy in this case because Bob’s quantum computer was connected to Alice’s black hole by a short wormhole when she threw her qubit inside.
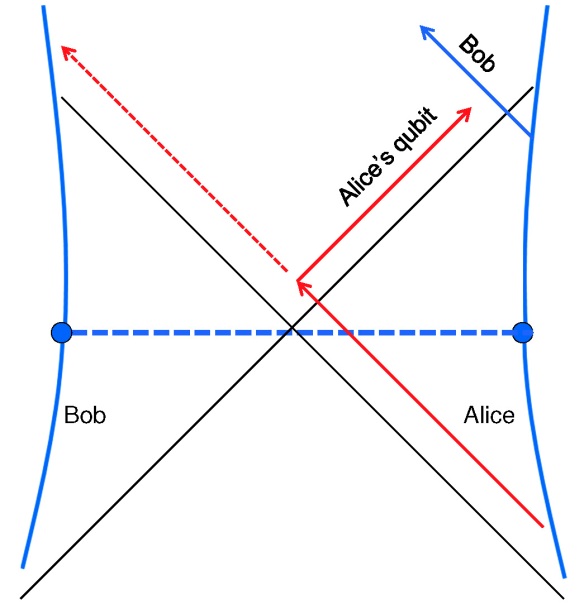
If, after a delay, Bob’s jumps into the black hole, he might find Alice’s qubit inside. But if he does, that qubit cannot be decoded by Bob’s quantum computer. Bob has no way to attain two copies of the qubit.
And what if Bob conducts his daring experiment, in which he decodes Alice’s qubit while still outside the black hole, and then jumps into the black hole to check whether the same qubit is also still inside? The above spacetime diagram contrasts two possible outcomes of Bob’s experiment. After entering the black hole, Alice might throw her qubit toward Bob so he can catch it inside the black hole. But if she does, then the qubit never reaches Bob’s quantum computer, and he won’t be able to decode it from the outside. On the other hand, Alice might allow her qubit to reach Bob’s quantum computer at the other end of the (now traversable) wormhole. But if she does, Bob won’t find the qubit when he enters the black hole. Either way, there is just one copy of the qubit, and no way to clone it. I shouldn’t have been so worried!
Granted, we have only described what happens in an oversimplified model of a black hole, but the lessons learned may be more broadly applicable. The case for broader applicability rests on a highly speculative idea, what Maldacena and Susskind called the ER=EPR conjecture, which I wrote about in this earlier blog post. One consequence of the conjecture is that a black hole highly entangled with a quantum computer is equivalent, after a transformation acting only on the computer, to two black holes connected by a short wormhole (though it might be difficult to actually execute that transformation). The insights of Gao-Jafferis-Wall and Maldacena-Stanford-Yang, together with the ER=EPR viewpoint, indicate that we don’t have to worry about the same quantum information being in two places at once. Quantum mechanics can survive the attack of the clones. Whew!
Thanks to Juan, Douglas, and Lenny for ongoing discussions and correspondence which have helped me to understand their ideas (including a lucid explanation from Douglas at our Caltech group meeting last Wednesday). This story is still unfolding and there will be more to say. These are exciting times!
