Little ray of sunshine

Posted on July 27, 2025 by Nicole Yunger Halpern

A common saying goes, you should never meet your heroes, because they’ll disappoint you. But you shouldn’t trust every common saying; some heroes impress you more, the better you know them. Ray Laflamme was such a hero.

I first heard of Ray in my undergraduate quantum-computation course. The instructor assigned two textbooks: the physics-centric “Schumacher and Westmoreland” and “Kaye, Laflamme, and Mosca,” suited to computer scientists. Back then—in 2011—experimentalists were toiling over single quantum logic gates, implemented on pairs and trios of qubits. Some of today’s most advanced quantum-computing platforms, such as ultracold atoms, resembled the scrawnier of the horses at a racetrack. My class studied a stepping stone to those contenders: linear quantum optics (quantum light). Laflamme, as I knew him then, had helped design the implementation.

Imagine my awe upon meeting Ray the following year, as a master’s student at the Perimeter Institute for Theoretical Physics. He belonged to Perimeter’s faculty and served as a co-director of the nearby Institute for Quantum Computing (IQC). Ray was slim, had thinning hair of a color similar to mine, and wore rectangular glasses frames. He often wore a smile, too. I can hear his French-Canadian accent in my memory, but not without hearing him smile at the ends of most sentences.

My master’s program entailed a research project, which I wanted to center on quantum information theory, one of Ray’s specialties. He met with me and suggested a project, and I began reading relevant papers. I then decided to pursue research with another faculty member and a postdoc, eliminating my academic claim on Ray’s time. But he agreed to keep meeting with me. Heaven knows how he managed; institute directorships devour one’s schedule like ravens dining on a battlefield. Still, we talked approximately every other week.

My master’s program intimidated me, I confessed. It crammed graduate-level courses, which deserved a semester each, into weeks. My class raced through Quantum Field Theory I and Quantum Field Theory II—a year’s worth of material—in part of an autumn. General relativity, condensed matter, and statistical physics swept over us during the same season. I preferred to learn thoroughly, deeply, and using strategies I’d honed over two decades. But I didn’t have time, despite arriving at Perimeter’s library at 8:40 every morning and leaving around 9:30 PM.

In response, Ray confessed that his master’s program had intimidated him. Upon completing his undergraduate degree, Ray viewed himself as a nobody from nowhere. He chafed in the legendary, if idiosyncratically named, program he attended afterward: Part III of the Mathematical Tripos at the University of Cambridge. A Cambridge undergraduate can earn a master’s degree in three steps (tripos) at the Department of Applied Mathematics and Theoretical Physics. Other students, upon completing bachelor’s degrees elsewhere, undertake the third step to earn their master’s. Ray tackled this step, Part III.

He worked his rear off, delving more deeply into course material than lecturers did. Ray would labor over every premise in a theorem’s proof, including when nobody could explain the trickiest step to him.¹ A friend and classmate helped him survive. The two studied together, as I studied with a few fellow Perimeter students; and Ray took walks with his friend on Sundays, as I planned lunches with other students on weekends.

Yet the program’s competitiveness appalled Ray. All students’ exam scores appeared on the same piece of paper, posted where everyone could read it. The department would retain the highest scorers in its PhD program; the other students would have to continue their studies elsewhere. Hearing about Ray’s program, I appreciated more than ever the collaboration characteristic of mine.

Ray addressed that trickiest proof step better than he’d feared, come springtime: his name appeared near the top of the exam list. Once he saw the grades, a faculty member notified him that his PhD advisor was waiting upstairs. Ray didn’t recall climbing those stairs, but he found Stephen Hawking at the top.

As one should expect of a Hawking student, Ray studied quantum gravity during his PhD. But by the time I met him, Ray had helped co-found quantum computation. He’d also extended his physics expertise as far from 1980s quantum gravity as one can, by becoming an experimentalist. The nobody from nowhere had earned his wings—then invented novel wings that nobody had dreamed of. But he descended from the heights every other week, to tell stories to a nobody of a master’s student.

The author’s copy of “Kaye, Laflamme, and Mosca”…

Seven and a half years later, I advertised openings in the research group I was establishing in Maryland. A student emailed from the IQC, whose co-directorship Ray had relinquished in 2017. The student had seen me present a talk, it had inspired him to switch fields into quantum thermodynamics, and he asked me to co-supervise his PhD. His IQC supervisor had blessed the request: Ray Laflamme.

The student was Shayan Majidy, now a postdoc at Harvard. Co-supervising him with Ray Laflamme reminded me of cooking in the same kitchen as Julia Child. I still wonder how I, green behind the ears, landed such a gig. Shayan delighted in describing the difference between his supervisors’ advising styles. An energetic young researcher,² I’d respond to emails as early as 6:00 AM. I’d press Shayan about literature he’d read, walk him through what he hadn’t grasped, and toss a paper draft back and forth with him multiple times per day. Ray, who’d mellowed during his career, mostly poured out support and warmth like hollandaise sauce.

Once, Shayan emailed Ray and me to ask if he could take a vacation. I responded first, as laconically as my PhD advisor would have: “Have fun!” Ray replied a few days later. He elaborated on his pleasure at Shayan’s plans and on how much Shayan deserved the break.

When I visited Perimeter in 2022, Shayan insisted on a selfie with both his PhD advisors.

This June, an illness took Ray earlier than expected. We physicists lost an intellectual explorer, a co-founder of the quantum-computing community, and a scientist of my favorite type: a wonderful physicist who was a wonderful human being. Days after he passed, I was holed up in a New York hotel room, wincing over a web search. I was checking whether a quantum system satisfies certain tenets of quantum error correction, and we call those tenets the Knill–Laflamme conditions. Our community will keep checking the Knill–Laflamme conditions, keep studying quantum gates implementable with linear optics, and more. Part of Ray won’t leave us anytime soon—the way he wouldn’t leave a nobody of a master’s student who needed a conversation.

¹For the record, some of the most rigorous researchers I know work in Cambridge’s Department of Applied Mathematics and Theoretical Physics today. I’ve even blogged about some.

²As I still am, thank you very much.

A (quantum) complex legacy: Part trois

Posted on June 22, 2025 by Nicole Yunger Halpern

When I worked in Cambridge, Massachusetts, a friend reported that MIT’s postdoc association had asked its members how it could improve their lives. The friend confided his suggestion to me: throw more parties.¹ This year grants his wish on a scale grander than any postdoc association could. The United Nations has designated 2025 as the International Year of Quantum Science and Technology (IYQ), as you’ve heard unless you live under a rock (or without media access—which, come to think of it, sounds not unappealing).

A metaphorical party cracker has been cracking since January. Governments, companies, and universities are trumpeting investments in quantum efforts. Institutions pulled out all the stops for World Quantum Day, which happens every April 14 but which scored a Google doodle this year. The American Physical Society (APS) suffused its Global Physics Summit in March with quantum science like a Bath & Body Works shop with the scent of Pink Pineapple Sunrise. At the summit, special symposia showcased quantum research, fellow blogger John Preskill dished about quantum-science history in a dinnertime speech, and a “quantum block party” took place one evening. I still couldn’t tell you what a quantum block party is, but this one involved glow sticks.

Attending the summit, I felt a satisfaction—an exultation, even—redolent of twelfth grade, when American teenagers summit the Mont Blanc of high school. It was the feeling that this year is our year. Pardon me while I hum “Time of your life.”²

Speakers and organizer of a Kavli Symposium, a special session dedicated to interdisciplinary quantum science, at the APS Global Physics Summit

Just before the summit, editors of the journal PRX Quantum released a special collection in honor of the IYQ.³ The collection showcases a range of advances, from chemistry to quantum error correction and from atoms to attosecond-length laser pulses. Collaborators and I contributed a paper about quantum complexity, a term that has as many meanings as companies have broadcast quantum news items within the past six months. But I’ve already published two Quantum Frontiers posts about complexity, and you surely study this blog as though it were the Bible, so we’re on the same page, right?

Just joshing.

Imagine you have a quantum computer that’s running a circuit. The computer consists of qubits, such as atoms or ions. They begin in a simple, “fresh” state, like a blank notebook. Post-circuit, they store quantum information, such as entanglement, as a notebook stores information post-semester. We say that the qubits are in some quantum state. The state’s quantum complexity is the least number of basic operations, such as quantum logic gates, needed to create that state—via the just-completed circuit or any other circuit.

Today’s quantum computers can’t create high-complexity states. The reason is, every quantum computer inhabits an environment that disturbs the qubits. Air molecules can bounce off them, for instance. Such disturbances corrupt the information stored in the qubits. Wait too long, and the environment will degrade too much of the information for the quantum computer to work. We call the threshold time the qubits’ lifetime, among more-obscure-sounding phrases. The lifetime limits the number of gates we can run per quantum circuit.

The ability to perform many quantum gates—to perform high-complexity operations—serves as a resource. Other quantities serve as resources, too, as you’ll know if you’re one of the three diehard Quantum Frontiers fans who’ve been reading this blog since 2014 (hi, Mom). Thermodynamic resources include work: coordinated energy that one can harness directly to perform a useful task, such as lifting a notebook or staying up late enough to find out what a quantum block party is.

My collaborators: Jonas Haferkamp, Philippe Faist, Teja Kothakonda, Jens Eisert, and Anthony Munson (in an order of no significance here)

My collaborators and I showed that work trades off with complexity in information- and energy-processing tasks: the more quantum gates you can perform, the less work you have to spend on a task, and vice versa. Qubit reset exemplifies such tasks. Suppose you’ve filled a notebook with a calculation, you want to begin another calculation, and you have no more paper. You have to erase your notebook. Similarly, suppose you’ve completed a quantum computation and you want to run another quantum circuit. You have to reset your qubits to a fresh, simple state.

Three methods suggest themselves. First, you can “uncompute,” reversing every quantum gate you performed.⁴ This strategy requires a long lifetime: the information imprinted on the qubits by a gate mustn’t leak into the environment before you’ve undone the gate.

Second, you can do the quantum equivalent of wielding a Pink Pearl Paper Mate: you can rub the information out of your qubits, regardless of the circuit you just performed. Thermodynamicists inventively call this strategy erasure. It requires thermodynamic work, just as applying a Paper Mate to a notebook does.

Third, you can

Suppose your qubits have finite lifetimes. You can undo as many gates as you have time to. Then, you can erase the rest of the qubits, spending work. How does complexity—your ability to perform many gates—trade off with work? My collaborators and I quantified the tradeoff in terms of an entropy we invented because the world didn’t have enough types of entropy.⁵

Complexity trades off with work not only in qubit reset, but also in data compression and likely other tasks. Quantum complexity, my collaborators and I showed, deserves a seat at the great soda fountain of quantum thermodynamics.

The great soda fountain of quantum thermodynamics

…as quantum information science deserves a seat at the great soda fountain of physics. When I embarked upon my PhD, faculty members advised me to undertake not only quantum-information research, but also some “real physics,” such as condensed matter. The latter would help convince physics departments that I was worth their money when I applied for faculty positions. By today, the tables have turned. A condensed-matter theorist I know has wound up an electrical-engineering professor because he calculates entanglement entropies.

So enjoy our year, fellow quantum scientists. Party like it’s 1925. Burnish those qubits—I hope they achieve the lifetimes of your life.

¹Ten points if you can guess who the friend is.

²Whose official title, I didn’t realize until now, is “Good riddance.” My conception of graduation rituals has just turned a somersault.

³PR stands for Physical Review, the brand of the journals published by the APS. The APS may have intended for the X to evoke exceptional, but I like to think it stands for something more exotic-sounding, like ex vita discedo, tanquam ex hospitio, non tanquam ex domo.

⁴Don’t ask me about the notebook analogue of uncomputing a quantum state. Explaining it would require another blog post.

⁵For more entropies inspired by quantum complexity, see this preprint. You might recognize two of the authors from earlier Quantum Frontiers posts if you’re one of the three…no, not even the three diehard Quantum Frontiers readers will recall; but trust me, two of the authors have received nods on this blog before.

Congratulations, class of 2025! Words from a new graduate

Posted on June 9, 2025 by jleschack

Editor’s note (Nicole Yunger Halpern): Jade LeSchack, the Quantum Steampunk Laboratory’s first undergraduate, received her bachelor’s degree from the University of Maryland this spring. Kermit the Frog presented the valedictory address, but Jade gave the following speech at the commencement ceremony for the university’s College of Mathematical and Natural Sciences. Jade heads to the University of Southern California for a PhD in physics this fall.

Good afternoon, everyone. My name is Jade, and it is my honor and pleasure to speak before you.

Today, I’m graduating with my Bachelor of Science, but when I entered UMD, I had no idea what it meant to be a professional scientist or where my passion for quantum science would take me. I want you to picture where you were four years ago. Maybe you were following a long-held passion into college, or maybe you were excited to explore a new technical field. Since then, you’ve spent hours titrating solutions, debugging code, peering through microscopes, working out proofs, and all the other things our disciplines require of us. Now, we’re entering a world of uncertainty, infinite possibility, and lifelong connections. Let me elaborate on each of these.

First, there is uncertainty. Unlike simplified projectile motion, you can never predict the exact trajectory of your life or career. Plans will change, and unexpected opportunities will arise. Sometimes, the best path forward isn’t the one you first imagined. Our experiences at Maryland have prepared us to respond to the challenges and curveballs that life will throw at us. And, we’re going to get through the rough patches.

Second, let’s embrace the infinite possibilities ahead of us. While the concept of the multiverse is best left to the movies, it’s exciting to think about all the paths before us. We’ve each found our own special interests over the past four years here, but there’s always more to explore. Don’t put yourself in a box. You can be an artist and a scientist, an entrepreneur and a humanitarian, an athlete and a scholar. Continue to redefine yourself and be open to your infinite potential.

Third, as we move forward, we are equipped not only with knowledge but with connections. We’ve made lasting relationships with incredible people here. As we go from place to place, the people who we’re close to will change. But we’re lucky that, these days, people are only an email or phone call away. We’ll always have our UMD communities rooting for us.

Now, the people we met here are certainly not the only important ones. We’ve each had supporters along the various stages of our journeys. These are the people who championed us, made sacrifices for us, and gave us a shoulder to cry on. I’d like to take a moment to thank all my mentors, teachers, and friends for believing in me. To my mom, dad, and sister sitting up there, I couldn’t have done this without you. Thank you for your endless love and support.

To close, I’d like to consider this age-old question that has always fascinated me: Is mathematics discovered or invented? People have made a strong case for each side. If we think about science in general, and our future contributions to our fields, we might ask ourselves: Are we discoverers or inventors? My answer is both! Everyone here with a cap on their head is going to contribute to both. We’re going to unearth new truths about nature and innovate scientific technologies that better society. This uncertain, multitudinous, and interconnected world is waiting for us, the next generation of scientific thinkers! So let’s be bold and stay fearless.

Congratulations to the class of 2024 and the class of 2025! We did it!

Author’s note: I was deeply grateful for the opportunity to serve as the student speaker at my commencement ceremony. I hope that the science-y references tickle the layman and SME alike. You can view a recording of the speech here. I can’t wait for my next adventures in quantum physics!

I know I am but what are you? Mind and Matter in Quantum Mechanics

Posted on May 27, 2025 by jeffreymepstein

Nowadays it is best to exercise caution when bringing the words “quantum” and “consciousness” anywhere near each other, lest you be suspected of mysticism or quackery. Eugene Wigner did not concern himself with this when he wrote his “Remarks on the Mind-Body Question” in 1967. (Perhaps he was emboldened by his recent Nobel prize for contributions to the mathematical foundations of quantum mechanics, which gave him not a little no-nonsense technical credibility.) The mind-body question he addresses is the full-blown philosophical question of “the relation of mind to body”, and he argues unapologetically that quantum mechanics has a great deal to say on the matter. The workhorse of his argument is a thought experiment that now goes by the name “Wigner’s Friend”. About fifty years later, Daniela Frauchiger and Renato Renner formulated another, more complex thought experiment to address related issues in the foundations of quantum theory. In this post, I’ll introduce Wigner’s goals and argument, and evaluate Frauchiger’s and Renner’s claims of its inadequacy, concluding that these are not completely fair, but that their thought experiment does do something interesting and distinct. Finally, I will describe a recent paper of my own, in which I formalize the Frauchiger-Renner argument in a way that illuminates its status and isolates the mathematical origin of their paradox.

* * *

Wigner takes a dualist view about the mind, that is, he believes it to be non-material. To him this represents the common-sense view, but is nevertheless a newly mainstream attitude. Indeed,

[until] not many years ago, the “existence” of a mind or soul would have been passionately denied by most physical scientists. The brilliant successes of mechanistic and, more generally, macroscopic physics and of chemistry overshadowed the obvious fact that thoughts, desires, and emotions are not made of matter, and it was nearly universally accepted among physical scientists that there is nothing besides matter.

He credits the advent of quantum mechanics with

the return, on the part of most physical scientists, to the spirit of Descartes’s “Cogito ergo sum”, which recognizes the thought, that is, the mind, as primary. [With] the creation of quantum mechanics, the concept of consciousness came to the fore again: it was not possible to formulate the laws of quantum mechanics in a fully consistent way without reference to the consciousness.

What Wigner has in mind here is that the standard presentation of quantum mechanics speaks of definite outcomes being obtained when an observer makes a measurement. Of course this is also true in classical physics. In quantum theory, however, the principles of linear evolution and superposition, together with the plausible assumption that mental phenomena correspond to physical phenomena in the brain, lead to situations in which there is no mechanism for such definite observations to arise. Thus there is a tension between the fact that we would like to ascribe particular observations to conscious agents and the fact that we would like to view these observations as corresponding to particular physical situations occurring in their brains.

Once we have convinced ourselves that, in light of quantum mechanics, mental phenomena must be considered on an equal footing with physical phenomena, we are faced with the question of how they interact. Wigner takes it for granted that “if certain physico-chemical conditions are satisfied, a consciousness, that is, the property of having sensations, arises.” Does the influence run the other way? Wigner claims that the “traditional answer” is that it does not, but argues that in fact such influence ought indeed to exist. (Indeed this, rather than technical investigation of the foundations of quantum mechanics, is the central theme of his essay.) The strongest support Wigner feels he can provide for this claim is simply “that we do not know of any phenomenon in which one subject is influenced by another without exerting an influence thereupon”. Here he recalls the interaction of light and matter, pointing out that while matter obviously affects light, the effects of light on matter (for example radiation pressure) are typically extremely small in magnitude, and might well have been missed entirely had they not been suggested by the theory.

Quantum mechanics provides us with a second argument, in the form of a demonstration of the inconsistency of several apparently reasonable assumptions about the physical, the mental, and the interaction between them. Wigner works, at least implicitly, within a model where there are two basic types of object: physical systems and consciousnesses. Some physical systems (those that are capable of instantiating the “certain physico-chemical conditions”) are what we might call mind-substrates. Each consciousness corresponds to a mind-substrate, and each mind-substrate corresponds to at most one consciousness. He considers three claims (this organization of his premises is not explicit in his essay):

1. Isolated physical systems evolve unitarily.

2. Each consciousness has a definite experience at all times.

3. Definite experiences correspond to pure states of mind-substrates, and arise for a consciousness exactly when the corresponding mind-substrate is in the corresponding pure state.

The first and second assumptions constrain the way the model treats physical and mental phenomena, respectively. Assumption 1 is often paraphrased as the `”completeness of quantum mechanics”, while Assumption 2 is a strong rejection of solipsism – the idea that only one’s own mind is sure to exist. Assumption 3 is an apparently reasonable assumption about the relation between mental and physical phenomena.

With this framework established, Wigner’s thought experiment, now typically known as Wigner’s Friend, is quite straightforward. Suppose that an observer, Alice (to name the friend), is able to perform a measurement of some physical quantity $q$ of a particle, which may take two values, $0$ and $1$ . Assumption 1 tells us that if Alice performs this measurement when the particle is in a superposition state, the joint system of Alice’s brain and the particle will end up in an entangled state. Now Alice’s mind-substrate is not in a pure state, so by Assumption 3 does not have a definite experience. This contradicts Assumption 2. Wigner’s proposed resolution to this paradox is that in fact Assumption 1 is incorrect, and that there is an influence of the mental on the physical, namely objective collapse or, as he puts it, that the “statistical element which, according to the orthodox theory, enters only if I make an observation enters equally if my friend does”.

* * *

Decades after the publication of Wigner’s essay, Daniela Frauchiger and Renato Renner formulated a new thought experiment, involving observers making measurements of other observers, which they intended to remedy what they saw as a weakness in Wigner’s argument. In their words, “Wigner proposed an argument […] which should show that quantum mechanics cannot have unlimited validity”. In fact, they argue, Wigner’s argument does not succeed in doing so. They assert that Wigner’s paradox may be resolved simply by noting a difference in what each party knows. Whereas Wigner, describing the situation from the outside, does not initially know the result of his friend’s measurement, and therefore assigns the “absurd” entangled state to the joint system composed of both her body and the system she has measured, his friend herself is quite aware of what she has observed, and so assigns to the system either, but not both, of the states corresponding to definite measurement outcomes. “For this reason”, Frauchiger and Renner argue, “the Wigner’s Friend Paradox cannot be regarded as an argument that rules out quantum mechanics as a universally valid theory.”

This criticism strikes me as somewhat unfair to Wigner. In fact, Wigner’s objection to admitting two different states as equally valid descriptions is that the two states correspond to different sets of \textit{physical} properties of the joint system consisting of Alice and the system she measures. For Wigner, physical properties of physical systems are distinct from mental properties of consciousnesses. To engage in some light textual analysis, we can note that the word ‘conscious’, or ‘consciousness’, appears forty-one times in Wigner’s essay, and only once in Frauchiger and Renner’s, in the title of a cited paper. I have the impression that the authors pay inadequate attention to how explicitly Wigner takes a dualist position, including not just physical systems but also, and distinctly, consciousnesses in his ontology. Wigner’s argument does indeed achieve his goals, which are developed in the context of this strong dualism, and differ from the goals of Frauchiger and Renner, who appear not to share this philosophical stance, or at least do not commit fully to it.

Nonetheless, the thought experiment developed by Frauchiger and Renner does achieve something distinct and interesting. We can understand Wigner’s no-go theorem to be of the following form: “Within a model incorporating both mental and physical phenomena, a set of apparently reasonable conditions on how the model treats physical phenomena, mental phenomena, and their interaction cannot all be satisfied”. The Frauchiger-Renner thought experiment can be cast in the same form, with different choices about how to implement the model and which conditions to consider. The major difference in the model itself is that Frauchiger and Renner do not take consciousnesses to be entities in their own rights, but simply take some states of certain physical systems to correspond to conscious experiences. Within such a model, Wigner’s assumption that each mind has a single, definite conscious experience at all times seems far less natural than it did within his model, where consciousnesses are distinct entities from the physical systems that determine them. Thus Frauchiger and Renner need to weaken this assumption, which was so natural to Wigner. The weakening they choose is a sort of transitivity of theories of mind. In their words (Assumption C in their paper):

Suppose that agent A has established that “I am certain that agent A’, upon reasoning within the same theory as the one I am using, is certain that $x =\xi$ at time $t$ .” Then agent A can conclude that “I am certain that $x=\xi$ at time $t$ .”

Just as Assumption 3 above was, for Wigner, a natural restriction on how a sensible theory ought to treat mental phenomena, this serves as Frauchiger’s and Renner’s proposed constraint. Just as Wigner designed a thought experiment that demonstrated the incompatibility of his assumption with an assumption of the universal applicability of unitary quantum mechanics to physical systems, so do Frauchiger and Renner.

* * *

In my recent paper “Reasoning across spacelike surfaces in the Frauchiger-Renner thought experiment”, I provide two closely related formalizations of the Frauchiger-Renner argument. These are motivated by a few observations:

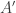1. Assumption C ought to make reference to the (possibly different) times at which agents $A$ and $A'$ are certain about their respective judgments, since these states of knowledge change.

2. Since Frauchiger and Renner do not subscribe to Wigner’s strong dualism, an agent’s certainty about a given proposition, like any other mental state, corresponds within their implicit model to a physical state. Thus statements like “Alice knows that P” should be understood as statements about the state of some part of Alice’s brain. Conditional statements like “if upon measuring a quantity q Alice observes outcome $x$ , she knows that P” should be understood as claims about the state of the composite system composed of the part of Alice’s brain responsible for knowing P and the part responsible for recording outcomes of the measurement of q.

3. Because the causal structure of the protocol does not depend on the absolute times of each event, an external agent describing the protocol can choose various “spacelike surfaces”, corresponding to fixed times in different spacetime embeddings of the protocol (or to different inertial frames). There is no reason to privilege one of these surfaces over another, and so each of them should be assigned a quantum state. This may be viewed as an implementation of a relativistic principle.

A visual representation of the formalization of the Frauchiger-Renner protocol and the arguments of the no-go theorem. The graphical conventions are explained in detail in “Reasoning across spacelike surfaces in the Frauchiger-Renner thought experiment”.

After developing a mathematical framework based on these observations, I recast Frauchiger’s and Renner’s Assumption C in two ways: first, in terms of a claim about the validity of iterating the “relative state” construction that captures how conditional statements are interpreted in terms of quantum states; and second, in terms of a deductive rule that allows chaining of inferences within a system of quantum logic. By proving that these claims are false in the mathematical framework, I provide a more formal version of the no-go theorem. I also show that the first claim can be rescued if the relative state construction is allowed to be iterated only “along” a single spacelike surface, and the second if a deduction is only allowed to chain inferences “along” a single surface. In other words, the mental transitivity condition desired by Frauchiger and Renner can in fact be combined with universal physical applicability of unitary quantum mechanics, but only if we restrict our analysis to a single spacelike surface. Thus I hope that the analysis I offer provides some clarification of what precisely is going on in Frauchiger and Renner’s thought experiment, what it tells us about combining the physical and the mental in light of quantum mechanics, and how it relates to Wigner’s thought experiment.

* * *

In view of the fact that “Quantum theory cannot consistently describe the use of itself” has, at present, over five hundred citations, and “Remarks on the Mind-Body Question” over thirteen hundred, it seems fitting to close with a thought, cautionary or exultant, from Peter Schwenger’s book on asemic, that is meaningless, writing. He notes that

commentary endlessly extends language; it is in the service of an impossible quest to extract the last, the final, drop of meaning.

I provide no analysis of this claim.

The most steampunk qubit

Posted on May 25, 2025 by Nicole Yunger Halpern

I never imagined that an artist would update me about quantum-computing research.

Last year, steampunk artist Bruce Rosenbaum forwarded me a notification about a news article published in Science. The article reported on an experiment performed in physicist Yiwen Chu’s lab at ETH Zürich. The experimentalists had built a “mechanical qubit”: they’d stored a basic unit of quantum information in a mechanical device that vibrates like a drumhead. The article dubbed the device a “steampunk qubit.”

I was collaborating with Bruce on a quantum-steampunk sculpture, and he asked if we should incorporate the qubit into the design. Leave it for a later project, I advised. But why on God’s green Earth are you receiving email updates about quantum computing?

My news feed sends me everything that says “steampunk,” he explained. So keeping a bead on steampunk can keep one up to date on quantum science and technology—as I’ve been preaching for years.

Other ideas displaced Chu’s qubit in my mind until I visited the University of California, Berkeley this January. Visiting Berkeley in January, one can’t help noticing—perhaps with a trace of smugness—the discrepancy between the temperature there and the temperature at home. And how better to celebrate a temperature difference than by studying a quantum-thermodynamics-style throwback to the 1800s?

One sun-drenched afternoon, I learned that one of my hosts had designed another steampunk qubit: Alp Sipahigil, an assistant professor of electrical engineering. He’d worked at Caltech as a postdoc around the time I’d finished my PhD there. We’d scarcely interacted, but I’d begun learning about his experiments in atomic, molecular, and optical physics then. Alp had learned about my work through Quantum Frontiers, as I discovered this January. I had no idea that he’d “met” me through the blog until he revealed as much to Berkeley’s physics department, when introducing the colloquium I was about to present.

Alp and collaborators proposed that a qubit could work as follows. It consists largely of a cantilever, which resembles a pendulum that bobs back and forth. The cantilever, being quantum, can have only certain amounts of energy. When the pendulum has a particular amount of energy, we say that the pendulum is in a particular energy level.

One might hope to use two of the energy levels as a qubit: if the pendulum were in its lowest-energy level, the qubit would be in its 0 state; and the next-highest level would represent the 1 state. A bit—a basic unit of classical information—has 0 and 1 states. A qubit can be in a superposition of 0 and 1 states, and so the cantilever could be.

A flaw undermines this plan, though. Suppose we want to process the information stored in the cantilever—for example, to turn a 0 state into a 1 state. We’d inject quanta—little packets—of energy into the cantilever. Each quantum would contain an amount of energy equal to (the energy associated with the cantilever’s 1 state) – (the amount associated with the 0 state). This equality would ensure that the cantilever could accept the energy packets lobbed at it.

But the cantilever doesn’t have only two energy levels; it has loads. Worse, all the inter-level energy gaps equal each other. However much energy the cantilever consumes when hopping from level 0 to level 1, it consumes that much when hopping from level 1 to level 2. This pattern continues throughout the rest of the levels. So imagine starting the cantilever in its 0 level, then trying to boost the cantilever into its 1 level. We’d probably succeed; the cantilever would probably consume a quantum of energy. But nothing would stop the cantilever from gulping more quanta and rising to higher energy levels. The cantilever would cease to serve as a qubit.

We can avoid this problem, Alp’s team proposed, by placing an atomic-force microscope near the cantilever. An atomic force microscope maps out surfaces similarly to how a Braille user reads: by reaching out a hand and feeling. The microscope’s “hand” is a tip about ten nanometers across. So the microscope can feel surfaces far more fine-grained than a Braille user can. Bumps embossed on a page force a Braille user’s finger up and down. Similarly, the microscope’s tip bobs up and down due to forces exerted by the object being scanned.

Imagine placing a microscope tip such that the cantilever swings toward it and then away. The cantilever and tip will exert forces on each other, especially when the cantilever swings close. This force changes the cantilever’s energy levels. Alp’s team chose the tip’s location, the cantilever’s length, and other parameters carefully. Under the chosen conditions, boosting the cantilever from energy level 1 to level 2 costs more energy than boosting from 0 to 1.

So imagine, again, preparing the cantilever in its 0 state and injecting energy quanta. The cantilever will gobble a quantum, rising to level 1. The cantilever will then remain there, as desired: to rise to level 2, the cantilever would have to gobble a larger energy quantum, which we haven’t provided.¹

Will Alp build the mechanical qubit proposed by him and his collaborators? Yes, he confided, if he acquires a student nutty enough to try the experiment. For when he does—after the student has struggled through the project like a dirigible through a hurricane, but ultimately triumphed, and a journal is preparing to publish their magnum opus, and they’re brainstorming about artwork to represent their experiment on the journal’s cover—I know just the aesthetic to do the project justice.

¹Chu’s team altered their cantilever’s energy levels using a superconducting qubit, rather than an atomic force microscope.

Quantum automata

Posted on April 27, 2025 by Nicole Yunger Halpern

Do you know when an engineer built the first artificial automaton—the first human-made machine that operated by itself, without external control mechanisms that altered the machine’s behavior over time as the machine undertook its mission?

The ancient Greek thinker Archytas of Tarentum reportedly created it about 2,300 years ago. Steam propelled his mechanical pigeon through the air.

For centuries, automata cropped up here and there as curiosities and entertainment. The wealthy exhibited automata to amuse and awe their peers and underlings. For instance, the French engineer Jacques de Vauconson built a mechanical duck that appeared to eat and then expel grains. The device earned the nickname the Digesting Duck…and the nickname the Defecating Duck.

Vauconson also invented a mechanical loom that helped foster the Industrial Revolution. During the 18th and 19th centuries, automata began to enable factories, which changed the face of civilization. We’ve inherited the upshots of that change. Nowadays, cars drive themselves, Roombas clean floors, and drones deliver packages.¹ Automata have graduated from toys to practical tools.²

Rather, classical automata have. What of their quantum counterparts?

Scientists have designed autonomous quantum machines, and experimentalists have begun realizing them. The roster of such machines includes autonomous quantum engines, refrigerators, and clocks. Much of this research falls under the purview of quantum thermodynamics, due to the roles played by energy in these machines’ functioning: above, I defined an automaton as a machine free of time-dependent control (exerted by a user). Equivalently, according to a thermodynamicist mentality, we can define an automaton as a machine on which no user performs any work as the machine operates. Thermodynamic work is well-ordered energy that can be harnessed directly to perform a useful task. Often, instead of receiving work, an automaton receives access to a hot environment and a cold environment. Heat flows from the hot to the cold, and the automaton transforms some of the heat into work.

Quantum automata appeal to me because quantum thermodynamics has few practical applications, as I complained in my previous blog post. Quantum thermodynamics has helped illuminate the nature of the universe, and I laud such foundational insights. Yet we can progress beyond laudation by trying to harness those insights in applications. Some quantum thermal machines—quantum batteries, engines, etc.—can outperform their classical counterparts, according to certain metrics. But controlling those machines, and keeping them cold enough that they behave quantum mechanically, costs substantial resources. The machines cost more than they’re worth. Quantum automata, requiring little control, offer hope for practicality.

To illustrate this hope, my group partnered with Simone Gasparinetti’s lab at Chalmer’s University in Sweden. The experimentalists created an autonomous quantum refrigerator from superconducting qubits. The quantum refrigerator can help reset, or “clear,” a quantum computer between calculations.

Artist’s conception of the autonomous-quantum-refrigerator chip. Credit: Chalmers University of Technology/Boid AB/NIST.

After we wrote the refrigerator paper, collaborators and I raised our heads and peered a little farther into the distance. What does building a useful autonomous quantum machine take, generally? Collaborators and I laid out guidelines in a “Key Issues Review” published in Reports in Progress on Physics last November.

We based our guidelines on DiVincenzo’s criteria for quantum computing. In 1996, David DiVincenzo published seven criteria that any platform, or setup, must meet to serve as a quantum computer. He cast five of the criteria as necessary and two criteria, related to information transmission, as optional. Similarly, our team provides ten criteria for building useful quantum automata. We regard eight of the criteria as necessary, at least typically. The final two, optional guidelines govern information transmission and machine transportation.

Time-dependent external control and autonomy

DiVincenzo illustrated his criteria with multiple possible quantum-computing platforms, such as ions. Similarly, we illustrate our criteria in two ways. First, we show how different quantum automata—engines, clocks, quantum circuits, etc.—can satisfy the criteria. Second, we illustrate how quantum automata can consist of different platforms: ultracold atoms, superconducting qubits, molecules, and so on.

Nature has suggested some of these platforms. For example, our eyes contain autonomous quantum energy transducers called photoisomers, or molecular switches. Suppose that such a molecule absorbs a photon. The molecule may use the photon’s energy to switch configuration. This switching sets off chemical and neurological reactions that result in the impression of sight. So the quantum switch transduces energy from light into mechanical, chemical, and electric energy.

Photoisomer. (Image by Todd Cahill, from *Quantum Steampunk*.)

My favorite of our criteria ranks among the necessary conditions: every useful quantum automata must produce output worth the input. How one quantifies a machine’s worth and cost depends on the machine and on the user. For example, an agent using a quantum engine may care about the engine’s efficiency, power, or efficiency at maximum power. Costs can include the energy required to cool the engine to the quantum regime, as well as the control required to initialize the engine. The agent also chooses which value they regard as an acceptable threshold for the output produced per unit input. I like this criterion because it applies a broom to dust that we quantum thermodynamicists often hide under a rug: quantum thermal machines’ costs. Let’s begin building quantum engines that perform more work than they require to operate.

One might object that scientists and engineers are already sweating over nonautonomous quantum machines. Companies, governments, and universities are pouring billions of dollars into quantum computing. Building a full-scale quantum computer by hook or by crook, regardless of classical control, is costing enough. Eliminating time-dependent control sounds even tougher. Why bother?

Fellow Quantum Frontiers blogger John Preskill pointed out one answer, when I described my new research program to him in 2022: control systems are classical—large and hot. Consider superconducting qubits—tiny quantum circuits—printed on a squarish chip about the size of your hand. A control wire terminates on each qubit. The rest of the wire runs off the edge of the chip, extending to classical hardware standing nearby. One can fit only so many wires on the chip, so one can fit only so many qubits. Also, the wires, being classical, are hotter than the qubits should be. The wires can help decohere the circuits, introducing errors into the quantum information they store. The more we can free the qubits from external control—the more autonomy we can grant them—the better.

Besides, quantum automata exemplify quantum steampunk, as my coauthor Pauli Erker observed. I kicked myself after he did, because I’d missed the connection. The irony was so thick, you could have cut it with the retractible steel knife attached to a swashbuckling villain’s robotic arm. Only two years before, I’d read The Watchmaker of Filigree Street, by Natasha Pulley. The novel features a Londoner expatriate from Meiji Japan, named Mori, who builds clockwork devices. The most endearing is a pet-like octopus, called Katsu, who scrambles around Mori’s workshop and hoards socks.

Does the world need a quantum version of Katsu? Not outside of quantum-steampunk fiction…yet. But a girl can dream. And quantum automata now have the opportunity to put quantum thermodynamics to work.

¹And deliver pizzas. While visiting the University of Pittsburgh a few years ago, I was surprised to learn that the robots scurrying down the streets were serving hungry students.

²And minions of starving young scholars.

Quantum Algorithms: A Call To Action

Posted on April 20, 2025 by robbieking1000

Quantum computing finds itself in a peculiar situation. On the technological side, after billions of dollars and decades of research, working quantum computers are nearing fruition. But still, the number one question asked about quantum computers is the same as it was two decades ago: What are they good for? The honest answer reveals an elephant in the room: We don’t fully know yet. For theorists like me, this is an opportunity, a call to action.

Technological momentum

Suppose we do not have quantum computers in a few decades time. What will be the reason? It’s unlikely that we’ll encounter some insurmountable engineering obstacle. The theoretical basis of quantum error-correction is solid, and several platforms are approaching or below the error-correction threshold (Harvard, Yale, Google). Experimentalists believe today’s technology can scale to 100 logical qubits and $10^6$ gates—the megaquop era. If mankind spends $100 billion over the next few decades, it’s likely we could build a quantum computer.

A more concerning reason that quantum computing might fail is that there is not enough incentive to justify such a large investment in R&D and infrastructure. Let’s make a comparison to nuclear fusion. Like quantum hardware, they have challenging science and engineering problems to solve. However, if a nuclear fusion lab were to succeed in their mission of building a nuclear fusion reactor, the application would be self-evident. This is not the case for quantum computing—it is a sledgehammer looking for nails to hit.

Nevertheless, industry investment in quantum computing is currently accelerating. To maintain the momentum, it is critical to match investment growth and hardware progress with algorithmic capabilities. The time to discover quantum algorithms is now.

Empowered theorists

Theory research is forward-looking and predictive. Theorists such as Geoffrey Hinton laid the foundations of the current AI revolution. But decades later, with an abundance of computing hardware, AI has become much more of an empirical field. I look forward to the day that quantum hardware reaches a state of abundance, but that day is not yet here.

Today, quantum computing is an area where theorists have extraordinary leverage. A few pages of mathematics by Peter Shor inspired thousands of researchers, engineers and investors to join the field. Perhaps another few pages by someone reading this blog will establish a future of world-altering impact for the industry. There are not many places where mathematics has such potential for influence. An entire community of experimentalists, engineers, and businesses are looking to the theorists for ideas.

The Challenge

Traditionally, it is thought that the ideal quantum algorithm would exhibit three features. First, it should be provably correct, giving a guarantee that executing the quantum circuit reliably will achieve the intended outcome. Second, the underlying problem should be classically hard—the output of the quantum algorithm should be computationally hard to replicate with a classical algorithm. Third, it should be useful, with the potential to solve a problem of interest in the real world. Shor’s algorithm comes close to meeting all of these criteria. However, demanding all three in an absolute fashion may be unnecessary and perhaps even counterproductive to progress.

Provable correctness is important, since today we cannot yet empirically test quantum algorithms on hardware at scale. But what degree of evidence should we require for classical hardness? Rigorous proof of classical hardness is currently unattainable without resolving major open problems like P vs NP, but there are softer forms of proof, such as reductions to well-studied classical hardness assumptions.

I argue that we should replace the ideal of provable hardness with a more pragmatic approach: The quantum algorithm should outperform the best known classical algorithm that produces the same output by a super-quadratic speedup.¹ Emphasizing provable classical hardness might inadvertently impede the discovery of new quantum algorithms, since a truly novel quantum algorithm could potentially introduce a new classical hardness assumption that differs fundamentally from established ones. The back-and-forth process of proposing and breaking new assumptions is a productive direction that helps us triangulate where quantum advantage lies.

It may also be unproductive to aim directly at solving existing real-world problems with quantum algorithms. Fundamental computational tasks with quantum advantage are special and we have very few examples, yet they necessarily provide the basis for any eventual quantum application. We should search for more of these fundamental tasks and match them to applications later.

That said, it is important to distinguish between quantum algorithms that could one day provide the basis for a practically relevant computation, and those that will not. In the real world, computations are not useful unless they are verifiable or at least repeatable. For instance, consider a quantum simulation algorithm that computes a physical observable. If two different quantum computers run the simulation and get the same answer, one can be confident that this answer is correct and that it makes a robust prediction about the world. Some problems such as factoring are naturally easy to verify classically, but we can set the bar even lower: The output of a useful quantum algorithm should at least be repeatable by another quantum computer.

There is a subtle fourth requirement of paramount importance that is often overlooked, captured by the following litmus test: If given a quantum computer tomorrow, could you implement your quantum algorithm? In order to do so, you need not only a quantum algorithm but also a distribution over its inputs on which to run it. Classical hardness must then be judged in the average case over this distribution of inputs, rather than in the worst case.

I’ll end this section with a specific caution regarding quantum algorithms whose output is the expectation value of an observable. A common reason these proposals fail to be classically hard is that the expectation value exponentially concentrates over the distribution of inputs. When this happens, a trivial classical algorithm can replicate the quantum result by simply outputting the concentrated (typical) value for every input. To avoid this, we must seek ensembles of quantum circuits whose expectation values exhibit meaningful variation and sensitivity to different inputs.

We can crystallize these priorities into the following challenge:

The Challenge
Find a quantum algorithm and a distribution over its inputs with the following features:
— (Provable correctness.) The quantum algorithm is provably correct.
— (Classical hardness.) The quantum algorithm outperforms the best known classical algorithm that performs the same task by a super-quadratic speedup, in the average-case over the distribution of inputs.
— (Potential utility.) The output is verifiable, or at least repeatable.

Examples and non-examples

Category	Classically verifiable	Quantumly repeatable	Potentially useful	Provable classical hardness	Examples
Search problem	Yes	Yes	Yes	No	Shor ‘99 Regev’s reduction: CLZ22, YZ24, Jor+24 Planted inference: Has20, SOKB24
Compute a value	No	Yes	Yes	No	Condensed matter physics? Quantum chemistry?
Proof of quantumness	Yes, with key	Yes, with respect to key	No	Yes, under crypto assumptions	BCMVV21
Sampling	No	No	No	Almost, under complexity assumptions	BJS10, AA11, Google ‘20

We can categorize quantum algorithms by the form of their output. First, there are quantum algorithms for search problems, which produce a bitstring satisfying some constraints. This could be the prime factors of a number, a planted feature in some dataset, or the solution to an optimization problem. Next, there are quantum algorithms that compute a value to some precision, for example the expectation value of some physical observable. Then there are proofs of quantumness, which involve a verifier who generates a test using some hidden key, and the key can be used to verify the output. Finally, there are quantum algorithms which sample from some distribution.

Hamiltonian simulation is perhaps the most widely heralded source of quantum utility. Physics and chemistry contain many quantities that Nature computes effortlessly, yet remain beyond the reach of even our best classical simulations. Quantum computation is capable of simulating Nature directly, giving us strong reason to believe that quantum algorithms can compute classically-hard quantities.

There are already many examples where a quantum computer could help us answer an unsolved scientific question, like determining the phase diagram of the Hubbard model or the ground energy of FeMoCo. These undoubtedly have scientific value. However, they are isolated examples, whereas we would like evidence that the pool of quantum-solvable questions is inexhaustible. Can we take inspiration from strongly correlated physics to write down a concrete ensemble of Hamiltonian simulation instances where there is a classically-hard observable? This would gather evidence for the sustained, broad utility of quantum simulation, and would also help us understand where and how quantum advantage arises.

Over in the computer science community, there has been a lot of work on oracle separations such as welded trees and forrelation, which should give us confidence in the abilities of quantum computers. Can we instantiate these oracles in a way that pragmatically remains classically hard? This is necessary in order to pass our earlier litmus test of being ready to run the quantum algorithm tomorrow.

In addition to Hamiltonian simulation, there are several other broad classes of quantum algorithms, including quantum algorithms for linear systems of equations and differential equations, variational quantum algorithms for machine learning, and quantum algorithms for optimization. These frameworks sometimes come with proofs of BQP-completeness.

The issue with these broad frameworks is that they often do not specify a distribution over inputs. Can we find novel ensembles of inputs to these frameworks which exhibit super-quadratic speedups? BQP-completeness shows that one has translated the notion of quantum computation into a different language, which allows one to embed an existing quantum algorithm such as Shor’s algorithm into your framework. But in order to discover a new quantum algorithm, you must find an ensemble of BQP computations which does not arise from Shor’s algorithm.

Table I claims that sampling tasks alone are not useful since they are not even quantumly repeatable. One may wonder if sampling tasks could be useful in some way. After all, classical Monte Carlo sampling algorithms are widely used in practice. However, applications of sampling typically use samples to extract meaningful information or specific features of the underlying distribution. For example, Monte Carlo sampling can be used to evaluate integrals in Bayesian inference and statistical physics. In contrast, samples obtained from random quantum circuits lack any discernible features. If a collection of quantum algorithms generated samples containing meaningful signals from which one could extract classically hard-to-compute values, those algorithms would effectively transition into the compute a value category.

Table I also claims that proofs of quantumness are not useful. This is not completely true—one potential application is generating certifiable randomness. However, such applications are generally cryptographic rather than computational in nature. Specifically, proofs of quantumness cannot help us solve problems or answer questions whose solutions we do not already know.

Finally, there are several exciting directions proposing applications of quantum technologies in sensing and metrology, communication, learning with quantum memory, and streaming. These are very interesting, and I hope that mankind’s second century of quantum mechanics brings forth all flavors of capabilities. However, the technological momentum is mostly focused on building quantum computers for the purpose of computational advantage, and so this is where breakthroughs will have the greatest immediate impact.

Don’t be too afraid

At the annual QIP conference, only a handful of papers out of hundreds each year attempt to advance new quantum algorithms. Given the stakes, why is this number so low? One common explanation is that quantum algorithm research is simply too difficult. Nevertheless, we have seen substantial progress in quantum algorithms in recent years. After an underwhelming lack of end-to-end proposals with the potential for utility between the years 2000 and 2020, Table I exhibits several breakthroughs from the past 5 years.

In between blind optimism and resigned pessimism, embracing a mission-driven mindset can propel our field forward. We should allow ourselves to adopt a more exploratory, scrappier approach: We can hunt for quantum advantages in yet-unstudied problems or subtle signals in the third decimal place. The bar for meaningful progress is lower than it might seem, and even incremental advances are valuable. Don’t be too afraid!

Quadratic speedups are widespread but will not form the basis of practical quantum advantage due to the overheads associated with quantum error-correction. ↩︎

How writing a popular-science book led to a Nature Physics paper

Posted on March 30, 2025 by Nicole Yunger Halpern

Several people have asked me whether writing a popular-science book has fed back into my research. Nature Physics published my favorite illustration of the answer this January. Here’s the story behind the paper.

In late 2020, I was sitting by a window in my home office (AKA living room) in Cambridge, Massachusetts. I’d drafted 15 chapters of my book Quantum Steampunk. The epilogue, I’d decided, would outline opportunities for the future of quantum thermodynamics. So I had to come up with opportunities for the future of quantum thermodynamics. The rest of the book had related foundational insights provided by quantum thermodynamics about the universe’s nature. For instance, quantum thermodynamics had sharpened the second law of thermodynamics, which helps explain time’s arrow, into more-precise statements. Conventional thermodynamics had not only provided foundational insights, but also accompanied the Industrial Revolution, a paragon of practicality. Could quantum thermodynamics, too, offer practical upshots?

Quantum thermodynamicists had designed quantum engines, refrigerators, batteries, and ratchets. Some of these devices could outperform their classical counterparts, according to certain metrics. Experimentalists had even realized some of these devices. But the devices weren’t useful. For instance, a simple quantum engine consisted of one atom. I expected such an atom to produce one electronvolt of energy per engine cycle. (A light bulb emits about 10²¹ electronvolts of light per second.) Cooling the atom down and manipulating it would cost loads more energy. The engine wouldn’t earn its keep.

Autonomous quantum machines offered greater hope for practicality. By autonomous, I mean, not requiring time-dependent external control: nobody need twiddle knobs or push buttons to guide the machine through its operation. Such control requires work—organized, coordinated energy. Rather than receiving work, an autonomous machine accesses a cold environment and a hot environment. Heat—random, disorganized energy cheaper than work—flows from the hot to the cold. The machine transforms some of that heat into work to power itself. That is, the machine sources its own work from cheap heat in its surroundings. Some air conditioners operate according to this principle. So can some quantum machines—autonomous quantum machines.

Thermodynamicists had designed autonomous quantum engines and refrigerators. Trapped-ion experimentalists had realized one of the refrigerators, in a groundbreaking result. Still, the autonomous quantum refrigerator wasn’t practical. Keeping the ion cold and maintaining its quantum behavior required substantial work.

My community needed, I wrote in my epilogue, an analogue of solar panels in southern California. (I probably drafted the epilogue during a Boston winter, thinking wistfully of Pasadena.) If you built a solar panel in SoCal, you could sit back and reap the benefits all year. The panel would fulfill its mission without further effort from you. If you built a solar panel in Rochester, you’d have to scrape snow off of it. Also, the panel would provide energy only a few months per year. The cost might not outweigh the benefit. Quantum thermal machines resembled solar panels in Rochester, I wrote. We needed an analogue of SoCal: an appropriate environment. Most of it would be cold (unlike SoCal), so that maintaining a machine’s quantum nature would cost a user almost no extra energy. The setting should also contain a slightly warmer environment, so that net heat would flow. If you deposited an autonomous quantum machine in such a quantum SoCal, the machine would operate on its own.

Where could we find a quantum SoCal? I had no idea.

Sunny SoCal. (Specifically, the Huntington Gardens.)

A few months later, I received an email from quantum experimentalist Simone Gasparinetti. He was setting up a lab at Chalmers University in Sweden. What, he asked, did I see as opportunities for experimental quantum thermodynamics? We’d never met, but we agreed to Zoom. Quantum Steampunk on my mind, I described my desire for practicality. I described autonomous quantum machines. I described my yearning for a quantum SoCal.

I have it, Simone said.

Simone and his colleagues were building a quantum computer using superconducting qubits. The qubits fit on a chip about the size of my hand. To keep the chip cold, the experimentalists put it in a dilution refrigerator. You’ve probably seen photos of dilution refrigerators from Google, IBM, and the like. The fridges tend to be cylindrical, gold-colored monstrosities from which wires stick out. (That is, they look steampunk.) You can easily develop the impression that the cylinder is a quantum computer, but it’s only the fridge.

The fridge, Simone said, resembles an onion: it has multiple layers. Outer layers are warmer, and inner layers are colder. The quantum computer sits in the innermost layer, so that it behaves as quantum mechanically as possible. But sometimes, even the fridge doesn’t keep the computer cold enough.

Imagine that you’ve finished one quantum computation and you’re preparing for the next. The computer has written quantum information to certain qubits, as you’ve probably written on scrap paper while calculating something in a math class. To prepare for your next math assignment, given limited scrap paper, you’d erase your scrap paper. The quantum computer’s qubits need erasing similarly. Erasing, in this context, means cooling down even more than the dilution refrigerator can manage.

Why not use an autonomous quantum refrigerator to cool the scrap-paper qubits?

I loved the idea, for three reasons. First, we could place the quantum refrigerator beside the quantum computer. The dilution refrigerator would already be cold, for the quantum computations’ sake. Therefore, we wouldn’t have to spend (almost any) extra work on keeping the quantum refrigerator cold. Second, Simone could connect the quantum refrigerator to an outer onion layer via a cable. Heat would flow from the warmer outer layer to the colder inner layer. From the heat, the quantum refrigerator could extract work. The quantum refrigerator would use that work to cool computational qubits—to erase quantum scrap paper. The quantum refrigerator would service the quantum computer. So, third, the quantum refrigerator would qualify as practical.

Over the next three years, we brought that vision to life. (By we, I mostly mean Simone’s group, as my group doesn’t have a lab.)

Postdoc Aamir Ali spearheaded the experiment. Then-master’s student Paul Jamet Suria and PhD student Claudia Castillo-Moreno assisted him. Maryland postdoc Jeffrey M. Epstein began simulating the superconducting qubits numerically, then passed the baton to PhD student José Antonio Marín Guzmán.

The experiment provided a proof of principle: it demonstrated that the quantum refrigerator could operate. The experimentalists didn’t apply the quantum refrigerator in a quantum computation. Also, they didn’t connect the quantum refrigerator to an outer onion layer. Instead, they pumped warm photons to the quantum refrigerator via a cable. But even in such a stripped-down experiment, the quantum refrigerator outperformed my expectations. I thought it would barely lower the “scrap-paper” qubit’s temperature. But that qubit reached a temperature of 22 milliKelvin (mK). For comparison: if the qubit had merely sat in the dilution refrigerator, it would have reached a temperature of 45–70 mK. State-of-the-art protocols had lowered scrap-paper qubits’ temperatures to 40–49 mK. So our quantum refrigerator outperformed our competitors, through the lens of temperature. (Our quantum refrigerator cooled more slowly than they did, though.)

Simone, José Antonio, and I have followed up on our autonomous quantum refrigerator with a forward-looking review about useful autonomous quantum machines. Keep an eye out for a blog post about the review…and for what we hope grows into a subfield.

In summary, yes, publishing a popular-science book can benefit one’s research.

The first and second centuries of quantum mechanics

Posted on March 20, 2025 by preskill

At this week’s American Physical Society Global Physics Summit in Anaheim, California, John Preskill spoke at an event celebrating 100 years of groundbreaking advances in quantum mechanics. Here are his remarks.

Welcome, everyone, to this celebration of 100 years of quantum mechanics hosted by the Physical Review Journals. I’m John Preskill and I’m honored by this opportunity to speak today. I was asked by our hosts to express some thoughts appropriate to this occasion and to feel free to share my own personal journey as a physicist. I’ll embrace that charge, including the second part of it, perhaps even more that they intended. But over the next 20 minutes I hope to distill from my own experience some lessons of broader interest.

I began graduate study in 1975, the midpoint of the first 100 years of quantum mechanics, 50 years ago and 50 years after the discovery of quantum mechanics in 1925 that we celebrate here. So I’ll seize this chance to look back at where quantum physics stood 50 years ago, how far we’ve come since then, and what we can anticipate in the years ahead.

As an undergraduate at Princeton, I had many memorable teachers; I’ll mention just one: John Wheeler, who taught a full-year course for sophomores that purported to cover all of physics. Wheeler, having worked with Niels Bohr on nuclear fission, seemed implausibly old, though he was actually 61. It was an idiosyncratic course, particularly because Wheeler did not refrain from sharing with the class his current research obsessions. Black holes were a topic he shared with particular relish, including the controversy at the time concerning whether evidence for black holes had been seen by astronomers. Especially notably, when covering the second law of thermodynamics, he challenged us to ponder what would happen to entropy lost behind a black hole horizon, something that had been addressed by Wheeler’s graduate student Jacob Bekenstein, who had finished his PhD that very year. Bekenstein’s remarkable conclusion that black holes have an intrinsic entropy proportional to the event horizon area delighted the class, and I’ve had had many occasions to revisit that insight in the years since then. The lesson being that we should not underestimate the potential impact of sharing our research ideas with undergraduate students.

Stephen Hawking made that connection between entropy and area precise the very next year when he discovered that black holes radiate; his resulting formula for black hole entropy, a beautiful synthesis of relativity, quantum theory, and thermodynamics ranks as one of the shining achievements in the first 100 years of quantum mechanics. And it raised a deep puzzle pointed out by Hawking himself with which we have wrestled since then, still without complete success — what happens to information that disappears inside black holes?

Hawking’s puzzle ignited a titanic struggle between cherished principles. Quantum mechanics tells us that as quantum systems evolve, information encoded in a system can get scrambled into an unrecognizable form, but cannot be irreversibly destroyed. Relativistic causality tells us that information that falls into a black hole, which then evaporates, cannot possibly escape and therefore must be destroyed. Who wins – quantum theory or causality? A widely held view is that quantum mechanics is the victor, that causality should be discarded as a fundamental principle. This calls into question the whole notion of spacetime — is it fundamental, or an approximate property that emerges from a deeper description of how nature works? If emergent, how does it emerge and from what? Fully addressing that challenge we leave to the physicists of the next quantum century.

I made it to graduate school at Harvard and the second half century of quantum mechanics ensued. My generation came along just a little too late to take part in erecting the standard model of particle physics, but I was drawn to particle physics by that intoxicating experimental and theoretical success. And many new ideas were swirling around in the mid and late 70s of which I’ll mention only two. For one, appreciation was growing for the remarkable power of topology in quantum field theory and condensed matter, for example the theory of topological solitons. While theoretical physics and mathematics had diverged during the first 50 years of quantum mechanics, they have frequently crossed paths in the last 50 years, and topology continues to bring both insight and joy to physicists. The other compelling idea was to seek insight into fundamental physics at very short distances by searching for relics from the very early history of the universe. My first publication resulted from contemplating a question that connected topology and cosmology: Would magnetic monopoles be copiously produced in the early universe? To check whether my ideas held water, I consulted not a particle physicist or a cosmologist, but rather a condensed matter physicist (Bert Halperin) who provided helpful advice. The lesson being that scientific opportunities often emerge where different subfields intersect, a realization that has helped to guide my own research over the following decades.

Looking back at my 50 years as a working physicist, what discoveries can the quantumists point to with particular pride and delight?

I was an undergraduate when Phil Anderson proclaimed that More is Different, but as an arrogant would be particle theorist at the time I did not appreciate how different more can be. In the past 50 years of quantum mechanics no example of emergence was more stunning than the fractional quantum Hall effect. We all know full well that electrons are indivisible particles. So how can it be that in a strongly interacting two-dimensional gas an electron can split into quasiparticles each carrying a fraction of its charge? The lesson being: in a strongly-correlated quantum world, miracles can happen. What other extraordinary quantum phases of matter await discovery in the next quantum century?

Another thing I did not adequately appreciate in my student days was atomic physics. Imagine how shocked those who elucidated atomic structure in the 1920s would be by the atomic physics of today. To them, a quantum measurement was an action performed on a large ensemble of similarly prepared systems. Now we routinely grab ahold of a single atom, move it, excite it, read it out, and induce pairs of atoms to interact in precisely controlled ways. When interest in quantum computing took off in the mid-90s, it was ion-trap clock technology that enabled the first quantum processors. Strong coupling between single photons and single atoms in optical and microwave cavities led to circuit quantum electrodynamics, the basis for today’s superconducting quantum computers. The lesson being that advancing our tools often leads to new capabilities we hadn’t anticipated. Now clocks are so accurate that we can detect the gravitational redshift when an atom moves up or down by a millimeter in the earth’s gravitational field. Where will the clocks of the second quantum century take us?

Surely one of the great scientific triumphs of recent decades has been the success of LIGO, the laser interferometer gravitational-wave observatory. If you are a gravitational wave scientist now, your phone buzzes so often to announce another black hole merger that it’s become annoying. LIGO would not be possible without advanced laser technology, but aside from that what’s quantum about LIGO? When I came to Caltech in the early 1980s, I learned about a remarkable idea (from Carl Caves) that the sensitivity of an interferometer can be enhanced by a quantum strategy that did not seem at all obvious — injecting squeezed vacuum into the interferometer’s dark port. Now, over 40 years later, LIGO improves its detection rate by using that strategy. The lesson being that theoretical insights can enhance and transform our scientific and technological tools. But sometimes that takes a while.

What else has changed since 50 years ago? Let’s give thanks for the arXiv. When I was a student few scientists would type their own technical papers. It took skill, training, and patience to operate the IBM typewriters of the era. And to communicate our results, we had no email or world wide web. Preprints arrived by snail mail in Manila envelopes, if you were lucky enough to be on the mailing list. The Internet and the arXiv made scientific communication far faster, more convenient, and more democratic, and LaTeX made producing our papers far easier as well. And the success of the arXiv raises vexing questions about the role of journal publication as the next quantum century unfolds.

I made a mid-career shift in research direction, and I’m often asked how that came about. Part of the answer is that, for my generation of particle physicists, the great challenge and opportunity was to clarify the physics beyond the standard model, which we expected to provide a deeper understanding of how nature works. We had great hopes for the new phenomenology that would be unveiled by the Superconducting Super Collider, which was under construction in Texas during the early 90s. The cancellation of that project in 1993 was a great disappointment. The lesson being that sometimes our scientific ambitions are thwarted because the required resources are beyond what society will support. In which case, we need to seek other ways to move forward.

And then the next year, Peter Shor discovered the algorithm for efficiently finding the factors of a large composite integer using a quantum computer. Though computational complexity had not been part of my scientific education, I was awestruck by this discovery. It meant that the difference between hard and easy problems — those we can never hope to solve, and those we can solve with advanced technologies — hinges on our world being quantum mechanical. That excited me because one could anticipate that observing nature through a computational lens would deepen our understanding of fundamental science. I needed to work hard to come up to speed in a field that was new to me — teaching a course helped me a lot.

Ironically, for 4 ½ years in the mid-1980s I sat on the same corridor as Richard Feynman, who had proposed the idea of simulating nature with quantum computers in 1981. And I never talked to Feynman about quantum computing because I had little interest in that topic at the time. But Feynman and I did talk about computation, and in particular we were both very interested in what one could learn about quantum chromodynamics from Euclidean Monte Carlo simulations on conventional computers, which were starting to ramp up in that era. Feynman correctly predicted that it would be a few decades before sufficient computational power would be available to make accurate quantitative predictions about nonperturbative QCD. But it did eventually happen — now lattice QCD is making crucial contributions to the particle physics and nuclear physics programs. The lesson being that as we contemplate quantum computers advancing our understanding of fundamental science, we should keep in mind a time scale of decades.

Where might the next quantum century take us? What will the quantum computers of the future look like, or the classical computers for that matter? Surely the qubits of 100 years from now will be much different and much better than what we have today, and the machine architecture will no doubt be radically different than what we can currently envision. And how will we be using those quantum computers? Will our quantum technology have transformed medicine and neuroscience and our understanding of living matter? Will we be building materials with astonishing properties by assembling matter atom by atom? Will our clocks be accurate enough to detect the stochastic gravitational wave background and so have reached the limit of accuracy beyond which no stable time standard can even be defined? Will quantum networks of telescopes be observing the universe with exquisite precision and what will that reveal? Will we be exploring the high energy frontier with advanced accelerators like muon colliders and what will they teach us? Will we have identified the dark matter and explained the dark energy? Will we have unambiguous evidence of the universe’s inflationary origin? Will we have computed the parameters of the standard model from first principles, or will we have convinced ourselves that’s a hopeless task? Will we have understood the fundamental constituents from which spacetime itself is composed?

There is an elephant in the room. Artificial intelligence is transforming how we do science at a blistering pace. What role will humans play in the advancement of science 100 years from now? Will artificial intelligence have melded with quantum intelligence? Will our instruments gather quantum data Nature provides, transduce it to quantum memories, and process it with quantum computers to discern features of the world that would otherwise have remained deeply hidden?

To a limited degree, in contemplating the future we are guided by the past. Were I asked to list the great ideas about physics to surface over the 50-year span of my career, there are three in particular I would nominate for inclusion on that list. (1) The holographic principle, our best clue about how gravity and quantum physics fit together. (2) Topological quantum order, providing ways to distinguish different phases of quantum matter when particles strongly interact with one another. (3) And quantum error correction, our basis for believing we can precisely control very complex quantum systems, including advanced quantum computers. It’s fascinating that these three ideas are actually quite closely related. The common thread connecting them is that all relate to the behavior of many-particle systems that are highly entangled.

Quantum error correction is the idea that we can protect quantum information from local noise by encoding the information in highly entangled states such that the protected information is inaccessible locally, when we look at just a few particles at a time. Topological quantum order is the idea that different quantum phases of matter can look the same when we observe them locally, but are distinguished by global properties hidden from local probes — in other words such states of matter are quantum memories protected by quantum error correction. The holographic principle is the idea that all the information in a gravitating three-dimensional region of space can be encoded by mapping it to a local quantum field theory on the two-dimensional boundary of the space. And that map is in fact the encoding map of a quantum error-correcting code. These ideas illustrate how as our knowledge advances, different fields of physics are converging on common principles. Will that convergence continue in the second century of quantum mechanics? We’ll see.

As we contemplate the long-term trajectory of quantum science and technology, we are hampered by our limited imaginations. But one way to loosely characterize the difference between the past and the future of quantum science is this: For the first hundred years of quantum mechanics, we achieved great success at understanding the behavior of weakly correlated many-particles systems relevant to for example electronic structure, atomic and molecular physics, and quantum optics. The insights gained regarding for instance how electrons are transported through semiconductors or how condensates of photons and atoms behave had invaluable scientific and technological impact. The grand challenge and opportunity we face in the second quantum century is acquiring comparable insight into the complex behavior of highly entangled states of many particles which are well beyond the reach of current theory or computation. This entanglement frontier is vast, inviting, and still largely unexplored. The wonders we encounter in the second century of quantum mechanics, and their implications for human civilization, are bound to supersede by far those of the first century. So let us gratefully acknowledge the quantum heroes of the past and present, and wish good fortune to the quantum explorers of the future.

Developing an AI for Quantum Chess: Part 1

Posted on March 16, 2025 by Chris Cantwell

In January 2016, Caltech’s Institute for Quantum Information and Matter unveiled a YouTube video featuring an extraordinary chess showdown between actor Paul Rudd (a.k.a. Ant-Man) and the legendary Dr. Stephen Hawking. But this was no ordinary match—Rudd had challenged Hawking to a game of Quantum Chess. At the time, Fast Company remarked, “Here we are, less than 10 days away from the biggest ~~advertising~~ football day of the year, and one of the best ads of the week is a 12-minute video of quantum chess from Caltech.” But a Super Bowl ad for what, exactly?

For the past nine years, Quantum Realm Games, with continued generous support from IQIM and other strategic partnerships, has been tirelessly refining the rudimentary Quantum Chess prototype showcased in that now-viral video, transforming it into a fully realized game—one you can play at home or even on a quantum computer. And now, at long last, we’ve reached a major milestone: the launch of Quantum Chess 1.0. You might be wondering—what took us so long?

The answer is simple: developing an AI capable of playing Quantum Chess.

Before we dive into the origin story of the first-ever AI designed to master a truly quantum game, it’s important to understand what enables modern chess AI in the first place.

Chess AI is a vast and complex field, far too deep to explore in full here. For those eager to delve into the details, the Chess Programming Wiki serves as an excellent resource. Instead, this post will focus on what sets Quantum Chess AI apart from its classical counterpart—and the unique challenges we encountered along the way.

So, let’s get started!

Depth Matters

credit: https://www.freecodecamp.org/news/simple-chess-ai-step-by-step-1d55a9266977/

With Chess AI, the name of the game is “depth”, at least for versions based on the Minimax strategy conceived by John von Neumann in 1928 (we’ll say a bit about Neural Network based AI later). The basic idea is that the AI will simulate the possible moves each player can make, down to some depth (number of moves) into the future, then decide which one is best based on a set of evaluation criteria (minimizing the maximum loss incurred by the opponent). The faster it can search, the deeper it can go. And the deeper it can go, the better its evaluation of each potential next move is.

Searching into the future can be modelled as a branching tree, where each branch represents a possible move from a given position (board configuration). The average branching factor for chess is about 35. That means that for a given board configuration, there are about 35 different moves to choose from. So if the AI looks 2 ply (moves) ahead, it sees 35×35 moves on average, and this blows up quickly. By 4 ply, the AI already has 1.5 million moves to evaluate.

Modern chess engines, like Stockfish and Leela, gain their strength by looking far into the future. Depth 10 is considered low in these cases; you really need 20+ if you want the engine to return an accurate evaluation of each move under consideration. To handle that many evaluations, these engines use strong heuristics to prune branches (the width of the tree), so that they don’t need to calculate the exponentially many leaves of the tree. For example, if one of the branches involves losing your Queen, the algorithm may decide to prune that branch and all the moves that come after. But as experienced players can see already, since a Queen sacrifice can sometimes lead to massive gains down the road, such a “naive” heuristic may need to be refined further before it is implemented. Even so, the tension between depth-first versus breadth-first search is ever present.

So I heard you like branches…

https://www.sciencenews.org/article/leonardo-da-vinci-rule-tree-branch-wrong-limb-area-thickness

The addition of split and merge moves in Quantum Chess absolutely explodes the branching factor. Early simulations have shown that it may be in the range of 100-120, but more work is needed to get an accurate count. For all we know, branching could be much bigger. We can get a sense by looking at a single piece, the Queen.

On an otherwise empty chess board, a single Queen on d4 has 27 possible moves (we leave it to the reader to find them all). In Quantum Chess, we add the split move: every piece, besides pawns, can move to any two empty squares it can reach legally. This adds every possible paired combination of standard moves to the list.

But wait, there’s more!

Order matters in Quantum Chess. The Queen can split to d3 and c4, but it can also split to c4 and d3. These subtly different moves can yield different underlying phase structures (given their implementation via a square-root iSWAP gate between the source square and the first target, followed by an iSWAP gate between the source and the second target), potentially changing how interference works on, say, a future merge move. So you get 27*26 = 702 possible moves! And that doesn’t include possible merge moves, which might add another 15-20 branches to each node of our tree.

Do the math and we see that there are roughly 30 times as many moves in Quantum Chess for that queen. Even if we assume the branching factor is only 100, by ply 4 we have 100 million moves to search. We obviously need strong heuristics to do some very aggressive pruning.

But where do we get strong heuristics for a new game? We don’t have centuries of play to study and determine which sequences of moves are good and which aren’t. This brings us to our first attempt at a Quantum Chess AI. Enter StoQfish.

StoQfish

Quantum Chess is based on chess (in fact, you can play regular Chess all the way through if you and your opponent decide to make no quantum moves), which means that chess skill matters. Could we make a strong chess engine work as a quantum chess AI? Stockfish is open source, and incredibly strong, so we started there.

Given the nature of quantum states, the first thing you think about when you try to adapt a classical strategy into a quantum one, is to split the quantum superposition underlying the state of the game into a series of classical states and then sample them according to their (squared) amplitude in the superposition. And that is exactly what we did. We used the Quantum Chess Engine to generate several chess boards by sampling the current state of the game, which can be thought of as a quantum superposition of classical chess configurations, according to the underlying probability distribution. We then passed these boards to Stockfish. Stockfish would, in theory, return its own weighted distribution of the best classical moves. We had some ideas on how to derive split moves from this distribution, but let’s not get ahead of ourselves.

This approach had limited success and significant failures. Stockfish is highly optimized for classical chess, which means that there are some positions that it cannot process. For example, consider the scenario where a King is in superposition of being captured and not captured; upon capture of one of these Kings, samples taken after such a move will produce boards without a King! Similarly, what if a King in superposition is in check, but you’re not worried because the other half of the King is well protected, so you don’t move to protect it? The concept of check is a problem all around, because Quantum Chess doesn’t recognize it. Things like moving “through check” are completely fine.

You can imagine then why whenever Stockfish encounters a board without a King it crashes. In classical Chess, there is always a King on the board. In Quantum Chess, the King is somewhere in the chess multiverse, but not necessarily in every board returned by the sampling procedure.

You might wonder if we couldn’t just throw away boards that weren’t valid. That’s one strategy, but we’re sampling probabilities so if we throw out some of the data, then we introduce bias into the calculation, which leads to poor outcomes overall.

We tried to introduce a King onto boards where he was missing, but that became its own computational problem: how do you reintroduce the King in a way that doesn’t change the assessment of the position?

We even tried to hack Stockfish to abandon its obsession with the King, but that caused a cascade of other failures, and tracing through the Stockfish codebase became a problem that wasn’t likely to yield a good result.

This approach wasn’t working, but we weren’t done with Stockfish just yet. Instead of asking Stockfish for the next best move given a position, we tried asking Stockfish to evaluate a position. The idea was that we could use the board evaluations in our own Minimax algorithm. However, we ran into similar problems, including the illegal position problem.

So we decided to try writing our own minimax search, with our own evaluation heuristics. The basics are simple enough. A board’s value is related to the value of the pieces on the board and their location. And we could borrow from Stockfish’s heuristics as we saw fit.

This gave us Hal 9000. We were sure we’d finally mastered quantum AI. Right? Find out what happened, in the next post.

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Technological momentum

Empowered theorists

The Challenge

Examples and non-examples

Don’t be too afraid

Share this:

Share this:

Share this:

Depth Matters

So I heard you like branches…

StoQfish

Share this: