The complementarity (not incompatibility) of reason and rhyme

Posted on by
8

Shortly after learning of the Institute for Quantum Information and Matter, I learned of its poetry.

I’d been eating lunch with a fellow QI student at the Perimeter Institute for Theoretical Physics. Perimeter’s faculty includes Daniel Gottesman, who earned his PhD at what became Caltech’s IQIM. Perhaps as Daniel passed our table, I wondered whether a liberal-arts enthusiast like me could fit in at Caltech.

“Have you seen Daniel Gottesman’s website?” my friend replied. “He’s written a sonnet.”

Quill

He could have written equations with that quill.

Digesting this news with my chicken wrap, I found the website after lunch. The sonnet concerned quantum error correction, the fixing of mistakes made during computations by quantum systems. After reading Daniel’s sonnet, I found John Preskill’s verses about Daniel. Then I found more verses of John’s.

To my Perimeter friend: You win. I’ll fit in, no doubt.

Exhibit A: the latest edition of The Quantum Times, the newsletter for the American Physical Society’s QI group. On page 10, my enthusiasm for QI bubbles over into verse. Don’t worry if you haven’t heard all the terms in the poem. Consider them guidebook entries, landmarks to visit during a Wikipedia trek.

If you know the jargon, listen to it with a newcomer’s ear. Does anyone other than me empathize with frustrated lattices? Or describe speeches accidentally as “monotonic” instead of as “monotonous”? Hearing jargon outside its natural habitat highlights how not to explain research to nonexperts. Examining names for mathematical objects can reveal properties that we never realized those objects had. Inviting us to poke fun at ourselves, the confrontation of jargon sprinkles whimsy onto the meringue of physics.

No matter your familiarity with physics or poetry: Enjoy. And fifty points if you persuade Physical Review Letters to publish this poem’s sequel.

Quantum information

By Nicole Yunger Halpern

If “CHSH” rings a bell,
you know QI’s fared, lately, well.
Such promise does this field portend!
In Neumark fashion, let’s extend
this quantum-information spring:
dilation, growth, this taking wing.

We span the space of physics types
from spin to hypersurface hype,
from neutron-beam experiment
to Bohm and Einstein’s discontent,
from records of a photon’s path
to algebra and other math
that’s more abstract and less applied—
of platforms’ details, purified.

We function as a refuge, too,
if lattices can frustrate you.
If gravity has got your goat,
momentum cutoffs cut your throat:
Forget regimes renormalized;
our states are (mostly) unit-sized.
Velocities stay mostly fixed;
results, at worst, look somewhat mixed.

Though factions I do not condone,
the action that most stirs my bones
is more a spook than Popov ghosts; 1
more at-a-distance, less quark-close.

This field’s a tot—cacophonous—
like cosine, not monotonous.
Cacophony enlivens thought:
We’ve learned from noise what discord’s not.

So take a chance on wave collapse;
enthuse about the CP maps;
in place of “part” and “piece,” say “bit”;
employ, as yardstick, Hilbert-Schmidt;
choose quantum as your nesting place,
of all the fields in physics space.

1 With apologies to Ludvig Faddeev.

Graphene gets serious

Posted on by
4

Imagine one marshmallow, 100 pieces of dried spaghetti, and a roll of masking tape lying on a large table. Next to the supplies are directions that read: “Elevate the marshmallow as high as possible using only the spaghetti and masking tape.” What was the first question that popped into your head? My assumption is your response had a disposition towards either “how can I do this?” or “why should I do this?” More precisely, your response probably could be whittled down to either a “how” or a “why.” If your first instinct was to ask yourself “how”, maybe an argument could be made that you are a natural problem solver, and that you welcome and genuinely are intrigued by challenges. If you asked “why”, then maybe you are someone who needs some good ‘ole fashioned incentive or a good extrinsic motive to perform well. Now imagine you were competing against three other people and the prize for the highest marshmallow was $100,000. Would the money motivate you to create a better structure, or would your relentless ambition towards excellence have been enough incentive for you to have placed your best foot forward from the outset? Undoubtedly, the money will make you think twice about your initial design ensuring your best effort, but my wish is to see more people performing at higher levels, not only due to monetary incentive, but also out of the sake of doing your best.

Chen-Chih Hsu & Benjamin Fackrell

Chen-Chih Hsu & Benjamin Fackrell

As humans, we are all naturally great problem solvers when compared, to say, any other known form of life on our planet. That is not to say, however, all humans choose to exercise those talents. Nonetheless, people do possess the ability to solve extremely complex problems, and I often wonder what makes some individuals face challenges head on with great heroism, while others whimper away with not as much as a grain of genuine interest or desire. I believe the reasons for different responses are connected with the way we individually have been taught to approach problems, and the amount of respect we have learned to award such methods. The attitude individuals possess when faced with a challenge can be shaped with encouragement from teachers and parents alike. When given an opportunity to educate students (of any age) regarding their attitude when faced with a problem, in that moment, we must teach absolute fearlessness. Attack the problem and take no prisoners, metaphorically speaking. Unfortunately, the prevailing attitude from the many students I work with daily is one of apathy and a play-it-safe approach with very little risk of making mistakes. For many students, forfeiting has greater power in protecting one’s reputation with peers and themselves than a courageous attempt that could end, in what they believe to be, an embarrassing mistake. I am always looking to instill a sense of honor, embracing a philosophy that a whole-hearted attempt merits infinitely more respect than a forfeit, and not to plan to fail, but prepare to stay the course in the case of an unfortunate event. My advice? Treat a failure like a fart; understand it’s sure to happen, try to find the humor in it, and keep moving forward. Mistakes can often indicate progress because if you are not making mistakes, per Albert Einstein, you must not be trying something new, consequently, you are not learning.
Continue reading →

What’s inside a black hole?

Posted on by
80

I have a multiple choice question for you.

What’s inside a black hole?

(A) An unlimited amount of stuff.
(B) Nothing at all.
(C) A huge but finite amount of stuff, which is also outside the black hole.
(D) None of the above.

The first three answers all seem absurd, boosting the credibility of (D). Yet … at the “Rapid Response Workshop” on black holes I attended last week at the KITP in Santa Barbara (and which continues this week), most participants were advocating some version of (A), (B), or (C), with varying degrees of conviction.

When physicists get together to talk about black holes, someone is bound to draw a cartoon like this one:

Penrose diagram depicting the causal structure of a black hole spacetime.

Part of a Penrose diagram depicting the causal structure of a black hole spacetime.

I’m sure I’ve drawn and contemplated some version of this diagram hundreds of times over the past 25 years in the privacy of my office, and many times in public discussions (including at least five times during the talk I gave at the KITP). This picture vividly captures the defining property of a black hole, found by solving Einstein’s classical field equations for gravitation: once you go inside there is no way out. Instead you are unavoidably drawn to the dreaded singularity, where known laws of physics break down (and the picture can no longer be trusted). If taken seriously, the picture says that whatever falls into a black hole is gone forever, at least from the perspective of observers who stay outside.

But for nearly 40 years now, we have known that black holes can shed their mass by emitting radiation, and presumably this process continues until the black hole disappears completely. If we choose to, we can maintain the black hole for as long as we please by feeding it new stuff at the same rate that radiation carries energy away. What I mean by option (A) is that  the radiation is completely featureless, carrying no information about what kind of stuff fell in. That means we can hide as much information as we please inside a black hole of a given mass.

On the other hand, the beautiful theory of black hole thermodynamics indicates that the entropy of a black hole is determined by its mass. For all other systems we know of besides black holes, the entropy of the system quantifies how much information we can hide in the system. If (A) is the right answer, then black holes would be fundamentally different in this respect, able to hide an unlimited amount of information even though their entropy is finite. Maybe that’s possible, but it would be rather disgusting, a reason to dislike answer (A).

There is another way to argue that (A) is not the right answer, based on what we call AdS/CFT duality. AdS just describes a consistent way to put a black hole in a “bottle,” so we can regard the black hole together with the radiation outside it as a closed system. Now, in gravitation it is crucial to focus on properties of spacetime that do not depend on the observer’s viewpoint; otherwise we can easily get very confused. The best way to be sure we have a solid way of describing things is to pay attention to what happens at the boundary of the spacetime, the walls of the bottle — that’s what CFT refers to. AdS/CFT provides us with tools for describing what happens when a black hole forms and evaporates, phrased entirely in terms of what happens on the walls of the bottle. If we can describe the physics perfectly by sticking to the walls of the bottle, always staying far away from the black hole, there doesn’t seem to be anyplace to hide an unlimited amount of stuff.

At the KITP, both Bill Unruh and Bob Wald argued forcefully for (A). They acknowledge the challenge of understanding the meaning of black hole entropy and of explaining why the AdS/CFT argument is wrong. But neither is willing to disavow the powerful message conveyed by that telling diagram of the black hole spacetime. As Bill said: “There is all that stuff that fell in and it crashed into the singularity and that’s it. Bye-bye.”

Adherents of (B) and (C) like to think about black hole physics from the perspective of an observer who stays outside the black hole. From that viewpoint, they say, the black hole behaves like any other system with a temperature and a finite entropy. Stuff falling in sticks to the black hole’s outer edge and gets rapidly mixed in with other stuff the black hole absorbed previously. For a black hole of a given mass, though, there is a limit to how much stuff it can hold. Eventually, what fell in comes out again, but in a form so highly scrambled as to be nearly unrecognizable.

Where the (B) and (C) camps differ concerns what happens to a brave observer who falls into a black hole. According to (C), an observer falling in crosses from the outside to the inside of a black hole peacefully, which poses a puzzle I discussed here. The puzzle arises because an uneventful crossing implies strong quantum entanglement between the region A just inside the black hole and region B just outside. On the other hand, as information leaks out of a black hole, region B should be strongly  entangled with the radiation system R emitted by the black hole long ago. Entanglement can’t be shared, so it does not make sense for B to be entangled with both A and R. What’s going on? Answer (C) resolves the puzzle by positing that A and R are not really different systems, but rather two ways to describe the same system, as I discussed here.That seems pretty crazy, because R could be far, far away from the black hole.

Answer (B) resolves the puzzle differently, by positing that region A does not actually exist, because the black hole has no interior. An observer who attempts to fall in gets a very rude surprise, striking a seething “firewall” at the last moment before passing to the inside. That seems pretty crazy, because no firewall is predicted by Einstein’s trusty equations, which are normally very successful at describing spacetime geometry.

At the workshop, Don Marolf and Raphael Bousso gave some new arguments supporting (B). Both acknowledge that we still lack a concrete picture of how firewalls are created as black holes form, but Bousso insisted that “It is time to constrain and construct the dynamics of firewalls.” Joe Polchinski emphasized that, while AdS/CFT provides a very satisfactory description of physics outside a black hole, it has not yet been able to tell us enough about the black hole interior to settle whether there are firewalls or not, at least for generic black holes formed from collapsing matter.

Lenny Susskind, Juan Maldacena, Ted Jacobson, and I all offered different perspectives on how (C) could turn out to be the right answer. We all told different stories, but perhaps each of us had at least part of the right answer. I’m not at KITP this week, but there have been further talks supporting (C) by Raju, Nomura, and the Verlindes.

I had a fun week at the KITP. If you watch the videos of the talks, you might get an occasional glimpse of me typing furiously on my laptop. It looks like I’m doing my email, but actually that’s how I take notes, which helps me to pay attention. Every once in a while I was inspired to tweet.

I have felt for a while that ideas from quantum information can help us to grasp the mysteries of quantum gravity, so I appreciated that quantum information concepts came up in many of the talks. Susskind invoked quantum error-correcting codes in discussing how sensitively the state of the Hawking radiation depends on the information it encodes, and Maldacena used tensor networks to explain how to build spacetime geometry from quantum entanglement. Scott Aaronson proposed the appropriate acronym HARD for HAwking Radiation Decoding, and argued (following Harlow and Hayden) that this task is as hard as inverting an injective one-way function, something we don’t expect quantum computers to be able to do.

In the organizational session that launched the meeting, Polchinski remarked regarding firewalls that “Nobody has the slightest idea what is going on,” and Gary Horowitz commented that “I’m still getting over the shock over how little we’ve learned in the past 30 years.” I guess that’s fair. Understanding what’s inside black holes has turned out to be remarkably subtle, making the problem more and more tantalizing. Maybe the current state of confusion regarding black hole information means that we’re on the verge of important discoveries about quantum gravity, or maybe not. In any case, invigorating discussions like what I heard last week are bound to facilitate progress.

The Most Awesome Animation About Quantum Computers You Will Ever See

Posted on by
44

by Jorge Cham

You might think the title is a little exaggerated, but if there’s one thing I’ve learned from Theoretical Physicists so far, it’s to be bold with my conjectures about reality.

Welcome to the second installment of our series of animations about Quantum Information! After an auspicious start describing doing the impossible, this week we take a step back to talk in general terms about what makes the Quantum World different and how these differences can be used to build Quantum Computers.

In this video, I interviewed John Preskill and Spiros Michalakis. John is the co-Director of the Institute for Quantum Information and Matter. He’s known for many things, including making (and winning) bets with Stephen Hawking. Spiros hails from Greece, and probably never thought he’d see himself drawn in a Faustian devil outfit in the name of science (although, he’s so motivated about outreach, he’d probably do it).

img_faust

In preparation to make this video, I thought I’d do what any serious writer would do to exhaustively research a complex topic like this: read the Wikipedia page and call it a day. But then, while visiting the local library with my son, I stumbled upon a small section of books about Quantum Physics aimed at a general audience.

I thought, “Great! I’ll read these books and learn that way!” When I opened the books, though, they were mostly all text. I’m not against text, but when you’re a busy* cartoonist on a deadline trying to learn one of the most complex topics humans have ever devised, a few figures would help. On the other hand, fewer graphics mean more job security for busy cartoonists, so I can’t really complain. (*=Not really).

img_god

In particular, I started to read “The Quantum Story: A History in 40 Moments” by Jim Baggott. First, telling a story in 40 moments sounds a lot like telling a story with comics, and second, I thought it would be great to learn about these concepts from the point of view of how they came up with them. So, I eagerly opened the book and here is what it says in the Preface:

“Nobody really understands how Quantum Theory actually works.”

“Niels Bohr claimed that anybody who is not shocked by the theory has not understood it… Richard Feynman went further: he claimed that nobody understands it.”

One page in, and it’s already telling me to give up.

It’s a fascinating read, I highly recommend the book. Baggott makes the claim that,

“The reality of Scientific Endeavor is profoundly messy, often illogical, deeply emotional, and driven by the individual personalities involved as they sleepwalk their way to a temporary scientific truth.”

I’m glad this history was recorded. I hope in a way that these videos help record a quantum of the developing story, as we humans try to create pockets of quantum weirdness that can scale up. As John says in the video, it is very exciting.

Now, if you’ll excuse me, I need to sleepwalk back to bed.

img_leaking

Watch the second installment of this series:

Jorge Cham is the creator of Piled Higher and Deeper (www.phdcomics.com).

CREDITS:

Featuring: John Preskill and Spiros Michalakis

Produced in Partnership with the Institute for Quantum Information and Matter (http://iqim.caltech.edu) at Caltech with funding provided by the National Science Foundation.

Animation Assistance: Meg Rosenburg
Transcription: Noel Dilworth

Steampunk quantum

Posted on by
22

A dark-haired man leans over a marble balustrade. In the ballroom below, his assistants tinker with animatronic elephants that trumpet and with potions for improving black-and-white photographs. The man is an inventor near the turn of the 20th century. Cape swirling about him, he watches technology wed fantasy.

Welcome to the steampunk genre. A stew of science fiction and Victorianism, steampunk has invaded literature, film, and the Wall Street Journal. A few years after James Watt improved the steam engine, protagonists build animatronics, clone cats, and time-travel. At sci-fi conventions, top hats and blast goggles distinguish steampunkers from superheroes.

Photo

The closest the author has come to dressing steampunk.

I’ve never read steampunk other than H. G. Wells’s The Time Machine—and other than the scene recapped above. The scene features in The Wolsenberg Clock, a novel by Canadian poet Jay Ruzesky. The novel caught my eye at an Ontario library.

In Ontario, I began researching the intersection of QI with thermodynamics. Thermodynamics is the study of energy, efficiency, and entropy. Entropy quantifies uncertainty about a system’s small-scale properties, given large-scale properties. Consider a room of air molecules. Knowing that the room has a temperature of 75°F, you don’t know whether some molecule is skimming the floor, poking you in the eye, or elsewhere. Ambiguities in molecules’ positions and momenta endow the gas with entropy. Whereas entropy suggests lack of control, work is energy that accomplishes tasks.
Continue reading →

Squeezing light using mechanical motion

Posted on by
1

This post is about generating a special type of light, squeezed light, using a mechanical resonator. But perhaps more importantly, it’s about an experiment (Caltech press release can be found here) that is very close to my heart: an experiment that brings to an end my career as a graduate student at Caltech and the IQIM, while paying homage to nearly four decades of work done by those before me at this institute.

The Quantum Noise of Light

First of all, what is squeezed light? It would be silly of me to imagine that I can provide a more clear and thorough explanation than what Jeff Kimble gave twenty years ago in Caltech’s Engineering and Science magazine. Instead, I’ll try to present what squeezing is in the context of optomechanics.

fig1

Quantization of light makes it noisy. Imagine a steady stream of water hitting a plate, and rolling off of it smoothly. The stream would indeed impart a steady force on the plate, but wouldn’t really cause it to “shake” around much. The plate would sense a steady pressure. This is what the classical theory of light, as proposed by James Clerk Maxwell, predicts. The effect is called radiation pressure. In the early 20th century, a few decades after this prediction, quantum theory came along and told us that “light is made of photons”. More or less, this means that a measurement capable of measuring the energy, power, or pressure imparted by light, if sensitive enough, will detect “quanta”, as if light were composed of particles. The force felt by a mirror is exactly this sort of measurement. To make sense of this, we can replace that mental image of a stream hitting a plate with one of the little raindrops hitting it, where each raindrop is a photon. Since the photons are coming in one at a time, and imparting their momentum all at once in little packets, they generate a new type of noise due to their random arrival times. This is called shot-noise (since the photons act as little “shots”). Since shot-noise is being detected here by the sound it generates due to the pressure imparted by light, we call it “Radiation Pressure Shot-Noise” (RPSN).
Continue reading →

Frozen children

Posted on by
6

Kids_watching_GlenA few weeks ago, my friend Amanda, an elementary school teacher who runs a children’s camp during the summer break, suggested that it could be fun for me to come into the camp one day and do some science demonstrations for the kids. I jumped at the opportunity, despite (or perhaps because of) the fact that I am a purely theoretical physicist and my day-to-day work only involves whiteboards and computers at Caltech. Most of the children attending the camp are relatively young (7-9 year-old kids) so, rather than setting out to give a science lesson, I viewed it as a chance to do some fun demonstrations and get these kids excited about science! Besides, I had an ulterior motive; it was a great excuse to acquire, and play with, liquid nitrogen (LN_2) from a Caltech lab (of which most of the IQIM labs have copious supplies). LN_2 is great for demonstrations; this stuff is awesome! At a temperature of -321^{\circ}\,F (for reference, the coldest temperature ever recorded on the surface of the Earth is -128.6^{\circ}\,F), it behaves in ways unlike anything that most people have ever seen. I convinced my friend Carmen, a postdoc in astronomy at Caltech, to come along and help out. Here, I thought I would share my experience, as well as some of the things I learned about handling LN_2.

Carmen watches on as I pour the liquid nitrogen into the beaker, which boils like crazy until the beaker is chilled. The white gas is actually water vapor condensing from the air; nitrogen gas is transparent (think of your ability to see through air). Note, also, my previous assistant in the background - science can be taxing to the body.

Carmen watches on as I pour the liquid nitrogen into the beaker, which boils like crazy until the beaker is chilled. The white gas is actually water vapor condensing from the air; nitrogen gas is transparent (think of your ability to see through air, which is mostly nitrogen gas).

DSC_0201

Liquid nitrogen volcano! All it takes is a little water added to the liquid nitrogen dewar.

Crime and punishment: As anyone who has seen Terminator 2 knows, objects that are pliable at room temperature become brittle and can shatter when reduced to cryogenic temperatures (including robotic assassins from the future). Thus I devoted a significant amount of the demonstration time to freezing and breaking everyday objects, including flowers and rubber toys. The flowers were particularly spectacular, shattering like glass into a multitude of pieces when struck against the table, providing a good deal of entertainment for the audience as well as myself. Hasta la vista, baby. I also froze several pennies, which then became brittle enough such that Carmen was able to shatter them with a few taps from a hammer. Incidentally, destroying US currency is illegal (which is why I had Carmen do it instead of doing it myself). I informed the children of this fact and asked who among them thought that Carmen should go to prison for her crime. A quick vote revealed that the majority of the children thought that she should be behind bars. Sorry Carmen, maybe the next field trip for the camp can be to visit you in prison?

DSC_0110

A flower, freshly pulled from the vat of liquid nitrogen, prepares to make the ultimate sacrifice in the name of science.

After having frozen a variety of objects, one of the children asked me whether you could freeze people with it. I told the kids that this is something that I always wanted to try, but that I had previously lacked a volunteer, to which an enthusiastic boy jumped up and responded, “freeze me, freeze me!” I asked whether he wanted to be frozen 5 years, 10 years, or longer? He said he would like to be frozen until the end of the world. One must admire his dedication! Before attempting to freeze him, I told him that it would be prudent for me to try it on something less likely to have litigious relatives. To this end a strawberry, a peach and a plum were submerged in LN_2, and then removed and allowed to slowly thaw. They ended up melting into gelatinous blobs; clearly some kinks in my cryogenic freezing and revival process need to be resolved before I graduate the approach to small children.
Continue reading →

Surviving in Extreme Conditions.

Posted on by
2

Sometimes in order to do one thing thoroughly you have to first master many other things, even those which may seem very unrelated to your focus. In the end, everything weaves itself together very elegantly and you find yourself wondering how you got through such an incredible sequence of coincidences to where you are now.

I am a rising first-year PhD student in Astrophysics at Caltech. I just completed my Bachelor’s in Physics also from Caltech last June. My Caltech journey has already led me to a number of unexpected places. New in Astrophysics, I am very excited to see as many observatories, labs and manufacturing locations as I can. I just moved out of the dorms and into the first place that is my very own home (which means I pay my own rent now). All of my windows have a very clear view of the radio tower-adorned Mt. Wilson.

This morning I woke up and looked at the Mt. Wilson horizon and decided to drive up there. I left my morning ballet class early to make time for the drive. The road to the observatory is not simple. HWY 2 is a pretty serious mountain road and accidents happen on it regularly. This is the first thing: to have access to observatories, I need to be able to drive there safely and reliably.

Fortunately I love driving, especially athletic mountain driving, so I am looking for almost any excuse to drive to JPL, Mt. Wilson, and so on. I’ll just stop, by saying that driving is a hobby for me and I see it as a sport, a science, and an art.

The first portion of the 2 is like any normal mountain road with speeding locals, terrifying cyclists and daredevil motorcyclists. The views become more and more breathtaking as you gain elevation, but the driver really shouldn’t be getting any of these views except for the portion that fits into the car’s field of view. The road is demanding, with turns and hills, all along a steep and curving mountainside. However, this part is a piece of cake compared to the second portion.

The turnoff to the observatory itself opens onto a less-maintained road speckled with enthusiastic hikers and with nicely sharp 6-inch pebbles scattered around the road. As much as I was enjoying taking smooth turns and avoiding the brakes, I went very slow on this section to drive around the random rocks on the road. I finally got to the top where I could take in the view in peace.

The first thing visitors see is the Cosmic Cafe. It has a balcony going all around the cafe with a fascinating view when there is no smog or fog. Last April, Caltech had its undergraduate student Formal here. We dined at this cafe and had a dance platform nearby. Driving up here, I could not help thinking how risky this was: 11 high-rise buses took a large portion of the Caltech undergraduate student body up to the top of this mountain in fog so dense we could barely see the bus ahead of us. The bus drivers were saints.

Hiking or running shoes are the best shoes to wear here, so I cannot imagine how we came here in suits, dress shoes, tight dresses, and merciless heels. Well, Caltech students have many talents. Second thing: being an active person in the Tech community takes you to some curious places on interesting occasions.

PAZ0101

Some Caltech undergraduates on Mt. Wilson (I’m purple).

I parked at the first available lot, right in front of the cafe and near some large radio towers. When trying to lock my car, I had some trouble. I have an electronic key which operates as a remote outside the car. The car would not react to my key and would not lock. I tried a few more times and finally it locked. I figured the battery in the key was dying, but that didn’t seem right. If any battery were dying, it would be the battery in the spare key that I am not using.
Continue reading →

On the importance of choosing a convenient basis

Posted on by
9

The benefits of Caltech’s proximity to Hollywood don’t usually trickle down to measly grad students like myself, except in the rare occasions when we befriend the industry’s technical contingent. One of my friends is a computer animator for Disney, which means that she designs algorithms enabling luxuriously flowing hair or trees with realistic lighting or feathers that have gorgeous texture, for movies like Wreck-it Ralph. Empowering computers to efficiently render scenes with these complicated details is trickier than you’d think and it requires sophisticated new mathematics. Fascinating conversations are one of the perks of having friends like this. But so are free trips to Disneyland! A couple nights ago, while standing in line for The Tower of Terror, I asked her what’s she’s currently working on. She’s very smart, as can be evidenced by her BS/MS in Computer Science/Mathematics from MIT, but she asked me if I “know about spherical harmonics.” Asking this to an aspiring quantum mechanic is like asking an auto mechanic if they know how to use a monkey wrench. She didn’t know what she was getting herself into!

me, LIGO, Disney

IQIM, LIGO, Disney

Along with this spherical harmonics conversation, I had a few other incidents last week that hammered home the importance of choosing a convenient basis when solving a scientific problem. First, my girlfriend works on LIGO and she’s currently writing her thesis. LIGO is a huge collaboration involving hundreds of scientists, and naturally, nobody there knows the detailed inner-workings of every subsystem. However, when it comes to writing the overview section of ones thesis, you need to at least make a good faith attempt to understand the whole behemoth. Anyways, my girlfriend recently asked if I know how the wavelet transform works. This is another example of a convenient basis, one that is particularly suited for analyzing abrupt changes, such as detecting the gravitational waves that would be emitted during the final few seconds of two black holes merging (ring-down). Finally, for the past couple weeks, I’ve been trying to understand entanglement entropy in quantum field theories. Most of the calculations that can be carried out explicitly are for the special subclass of quantum field theories called “conformal field theories,” which in two dimensions have a very convenient ‘basis’, the Virasoro algebra.

So why does a Disney animator care about spherical harmonics? It turns out that every frame that goes into one of Disney’s movies needs to be digitally rendered using a powerful computing cluster. The animated film industry has traded the painstaking process of hand-animators drawing every single frame, for the almost equally time-consuming process of computer clusters generating every frame. It doesn’t look like strong AI will be available in our immediate future, and in the meantime, humans are still much better than computers at detecting patterns and making intuitive judgements about the ‘physical correctness of an image.’ One of the primary advantages of computer animation is that an animator shouldn’t need to shade in every pixel of every frame — some of this burden should fall on computers. Let’s imagine a thought experiment. An animator wants to get the lighting correct for a nighttime indoor shot. They should be able to simply place the moon somewhere out of the shot, so that its glow can penetrate through the windows. They should also be able to choose from a drop down menu and tell the computer that a hand drawn lightbulb is a ‘light source.’ The computer should then figure out how to make all of the shadows and brightness appear physically correct. Another example of a hard problem is that an animator should be able to draw a character, then tell the computer that the hair they drew is ‘hair’, so that as the character moves through scenes, the physics of the hair makes sense. Programming computers do these things autonomously is harder than it sounds.

In the lighting example, imagine you want to get the lighting correct in a forest shot with complicated pine trees and leaf structures. The computer would need to do the ray-tracing for all of the photons emanating from the different light sources, and then the second-order effects as these photons reflect, and then third-order effects, etc. It’s a tall order to make the scene look accurate to the human eyeball/brain. Instead of doing all of this ray-tracing, it’s helpful to choose a convenient basis in order to dramatically speed up the processing. Instead of the complicated forest example, let’s imagine you are working with a tree from Super Mario Bros. Imagine drawing a sphere somewhere in the middle of this and then defining a ‘height function’, which outputs the ‘elevation’ of the tree foliage over each point on the sphere. I tried to use suggestive language, so that you’d draw an analogy to thinking of Earth’s ‘height function’ as the elevation of mountains and the depths of trenches over the sphere, with sea-level as a baseline. An example of how you could digitize this problem for a tree or for the earth is by breaking up the sphere into a certain number of pixels, maybe one per square meter for the earth (5*10^14 square meters gives approximately 2^49 pixels), and then associating an integer height value between [-2^15,2^15] to each pixel. This would effectively digitize the height map of the earth. In this case, keeping track of the elevation to approximately the meter level. But this leaves us with a huge amount of information that we need to store, and then process. We’d have to keep track of the height value for each pixel, giving us approximately 2^49*2^16=2^65 bits=4 exabytes that we’d have to keep track of. And this is for an easy static problem with only meter resolution! We can store this information much more efficiently using spherical harmonics.

mariotree

There are many ways to think about spherical harmonics. Basically, they’re functions which map points on the sphere to real numbers Y_l^m: (\theta,\phi) \mapsto Y_l^m(\theta,\phi)\in\mathbb{R}, such that they satisfy a few special properties. They are orthogonal, meaning that if you multiply two different spherical harmonics together and then integrate over the sphere, then you get zero. If you square one of the functions and then integrate over the sphere, you get a finite, nonzero value. This means that they are orthogonal functions. They also span the space of all height functions that one could define over the sphere. This means that for a planet with an arbitrarily complicated topography, you would be able to find some weighted combination of different spherical harmonics which perfectly describes that planet’s topography. These are the key properties which make a set of functions a basis: they span and are orthogonal (this is only a heuristic). There is also a natural way to think about the light that hits the tree. We can use the same sphere and simply calculate the light rays as they would hit the ideal sphere. With these two different ‘height functions’, it’s easy to calculate the shadows and brightness inside the tree. You simply convolve the two functions, which is a fast operation on a computer. It also means that if the breeze slightly changes the shape of the tree, or if the sun moves a little bit, then it’s very easy to update the shading. Implicit in what I just said, using spherical harmonics allows us to efficiently store this height map. I haven’t calculated this on a computer, but it doesn’t seem totally crazy to think that we’d be able to store the topography of the earth to a reasonable accuracy, with 100 nonzero coefficients of the spherical harmonics to 64 bits of precision, 2^7*2^6= 2^13 << 2^65. Where does this cost savings come from? It comes from the fact that the spherical harmonics are a convenient basis, which naturally encode the types of correlations we see in Earth’s topography — if you’re standing at an elevation of 2000m, the area within ten meters is probably at a similar elevation. Cliffs are what break this basis — but are what the wavelet basis was designed to handle.

I’ve only described a couple bases in this post and I’ve neglected to mention some of the most famous examples! This includes the Fourier basis, which was designed to encode periodic signals, such as music and radio waves. I also have not gone into any detail about the Virasoro algebra, which I mentioned at the beginning of this post, and I’ve been using it heavily for the past few weeks. For the sake of diversity, I’ll spend a few sentences whetting your apetite. Complex analysis is primarily the study of analytic functions. In two dimensions, these analytic functions “preserve angles.” This means that if you have two curves which intersect at a point with angle \theta, then after using an analytic function to map these curves to their image, also in the complex plane, then the angle between the curves will still be \theta. An especially convenient basis for the analytic functions in two-dimensions (\{f: \mathbb{C} \to \mathbb{C}\}, where f(z) = \sum_{n=0}^{\infty} a_nz^n) is given by the set of functions \{l_n = -z^{n+1}\partial_z\}. As always, I’m not being exactly precise, but this is a ‘basis’ because we can encode all the information describing an infinitesimal two-dimensional angle-preserving map using these elements. It turns out to have incredibly special properties, including that its quantum cousin yields something called the “central charge” which has deep ramifications in physics, such as being related to the c-theorem. Conformal field theories are fascinating because they describe the physics of phase transitions. Having a convenient basis in two-dimensions is a large part of why we’ve been able to make progress in our understanding of two-dimensional phase transitions (more important is that the 2d conformal symmetry group is infinite-dimensional, but that’s outside the scope of this post.) Convenient bases are also important for detecting gravitational waves, making incredible movies and striking up nerdy conversations in long lines at Disneyland!

 

Monopoles passing through Flatland!

Posted on by
7

Like many mathematically inclined teenagers, I was charmed when I first read the book Flatland by Edwin Abbott Abbott.* It’s a story about a Sphere who visits a two-dimensional world and tries to awaken its inhabitants to the existence of a third dimension. As perceived by Flatlanders, the Sphere is a circle which appears as a point, grows to maximum size, then shrinks and disappears.

My memories of Flatland were aroused as I read a delightful recent paper by Max Metlitski, Charlie Kane, and Matthew Fisher about magnetic monopoles and three-dimensional bosonic topological insulators. To explain why, I’ll need to recall a few elements of the theory of monopoles and of topological insulators, before returning to the connection between the two and why that reminds me of Flatland.

Flatlanders, confined to the surface of a topological insulator, are convinced by a magnetic monopole that there is a third dimension.

Flatlanders, confined to the two-dimensional surface of a topological insulator, are convinced by a magnetic monopole that a third dimension must exist.

Monopoles

Paul Dirac was no ordinary genius. Aside from formulating relativistic electron theory and predicting the existence of antimatter, Dirac launched the quantum theory of magnetic monopoles in a famous 1931 paper. Dirac envisioned a magnetic monopole as a semi-infinitely long, infinitesimally thin string of magnetic flux, such that the end of the string, where the flux spills out, seems to be a magnetic charge. For this picture to make sense, the string should be invisible. Dirac pointed out that an electron with electric charge e, transported around a string carrying flux 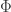\Phi, could detect the string (via what later came to be called the Aharonov-Bohm effect) unless the flux is an integer multiple of 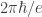2\pi\hbar /e, where 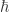\hbar is Planck’s constant. Conversely, in order for the string to be invisible, if a magnetic monopole exists with magnetic charge g_D = 2\pi\hbar /e, then all electric charges must be integer multiples of e. Thus the existence of magnetic monopoles (which have never been observed) could explain quantization of electric charge (which has been observed).

Captivated by the beauty of his own proposal, Dirac concluded his paper by remarking, “One would be surprised if Nature had made no use of it.”

Our understanding of quantized magnetic monopoles advanced again in 1979 when another extraordinary physicist, Edward Witten, discussed a generalization of Dirac’s quantization condition. Witten noted that the Lagrange density of electrodynamics could contain a term of the form

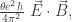
\frac{\theta e^2\hbar}{4\pi^2}~\vec{E}\cdot\vec{B},

where 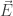\vec{E} is the electric field and \vec{B} is the magnetic field. This “\theta term” may also be expressed as

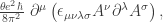
\frac{\theta e^2\hbar}{8\pi^2}~ \partial^\mu\left(\epsilon_{\mu\nu\lambda\sigma}A^\nu\partial^\lambda A^\sigma \right),

where A is the vector potential, and hence is a total derivative which makes no contribution to the classical field equations of electrodynamics. But Witten realized that it can have important consequences for the quantum properties of magnetic monopoles. Specifically, the \theta term modifies the field momentum conjugate to the vector potential, which becomes

\vec{E}+\frac{\theta e^2\hbar}{4\pi^2}\vec{B}.

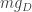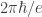Because the Gauss law condition satisfied by physical quantum states is altered, for a monopole with magnetic charge m g_D , where g_D is Dirac’s minimal charge 2\pi\hbar /e and m is an integer, the allowed values of the electric charge become

q = e\left( n - \frac{\theta m}{2\pi}\right),

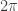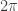where n is an integer. This spectrum of allowed charges remains invariant if \theta advances by 2\pi, suggesting that the parameter \theta is actually an angular variable with period 2\pi. This periodicity of \theta can be readily verified in a theory admitting fermions with the minimal charge e. But if the charged particles are bosons then \theta turns out to be a periodic variable with period 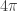4\pi instead.

That \theta has a different period for a bosonic theory than a fermionic one has an interesting interpretation. As Goldhaber noticed in 1976, dyons carrying both magnetic and electric charge can exhibit statistical transmutation. That is, in a purely bosonic theory, a dyon with magnetic charge g_D= 2\pi\hbar/e and electric charge ne is a fermion if n is an odd integer — when two dyons are exchanged, transport of each dyon’s electric charge in the magnetic field of the other dyon induces a sign change in the wave function. In a fermionic theory the story is different; now we can think of the dyon as a fermionic electric charge bound to a bosonic monopole. There are two canceling contributions to the exchange phase of the dyon, which is therefore a boson for any integer value of n, whether even or odd.

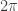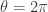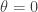As \theta smoothly increases from 0 to 2\pi, the statistics (whether bosonic or fermionic) of a dyon remains fixed even as the dyon’s electric charge increases by e. For the bosonic theory with \theta = 2\pi, then, dyons with magnetic charge g_D and electric charge ne are bosons for n odd and fermions for n even, the opposite of what happens when \theta=0. 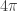For the bosonic theory, unlike the fermionic theory, we need to increase \theta by 4\pi for the physics of dyons to be fully invariant.

In 1979 Ed Witten was a postdoc at Harvard, where I was a student, though he was visiting CERN for the summer when he wrote his paper about the \theta-dependent monopole charge. I always read Ed’s papers carefully, but I gave special scrutiny to this one because magnetic monopoles were a pet interest of mine. At the time, I wondered whether the Witten effect might clarify how to realize the \theta parameter in a lattice gauge theory. But it certainly did not occur to me that the \theta-dependent electric charge of a magnetic monopole could have important implications for quantum condensed matter physics. Theoretical breakthroughs often have unexpected consequences, which may take decades to emerge.

Symmetry-protected topological phases

Okay, now let’s talk about topological insulators, a very hot topic in condensed matter physics these days. Actually, a topological insulator is a particular instance of a more general concept called a symmetry-protected topological phase of matter (or SPT phase). Consider a d-dimensional hunk of material with a (d-1)-dimensional boundary. If the material is in an SPT phase, then the physics of the d-dimensional bulk is boring — it’s just an insulator with an energy gap, admitting no low-energy propagating excitations. But the physics of the (d-1)-dimensional edge is exotic and exciting — for example the edge might support “gapless” excitations of arbitrarily low energy which can conduct electricity. The exotica exhibited by the edge is a consequence of a symmetry, and is destroyed if the symmetry is broken either explicitly or spontaneously; that is why we say the phase is “symmetry protected.”

The low-energy edge excitations can be described by a (d-1)-dimensional effective field theory. But for a typical SPT phase, this effective field theory is what we call anomalous, which means that for one reason or another the theory does not really make sense. The anomaly tells us something interesting and important, namely that the (d-1)-dimensional theory cannot be really, truly (d-1) dimensional; it can arise only at the edge of a higher-dimensional system.

This phenomenon, in which the edge does not make sense by itself without the bulk, is nicely illustrated by the integer quantum Hall effect, which occurs in a two-dimensional electron system in a high magnetic field and at low temperature, if the sample is sufficiently clean so that the electrons are highly mobile and rarely scattered by impurities. In this case the relevant symmetry is electron number, or equivalently the electric charge. At the one-dimensional edge of a two-dimensional quantum Hall sample, charge carriers move in only one direction — to the right, say, but not to the left. A theory with such chiral electric charges does not really make sense. One problem is that electric charge is not conserved — an electric field along the edge causes charge to be locally created, which makes the theory inconsistent.

The way the theory resolves this conundrum is quite remarkable. A two-dimensional strip of quantum Hall fluid has two edges, one at the top, the other at the bottom. While the top edge has only right-moving excitations, the bottom edge has only left-moving excitations. When electric charge appears on the top edge, it is simultaneously removed from the bottom edge. Rather miraculously, charge can be conveyed across the bulk from one edge to the other, even though the bulk does not have any low-energy excitations at all.

I first learned about this interplay of edge and bulk physics from a beautiful 1985 paper by Curt Callan and Jeff Harvey. They explained very lucidly how an edge theory with an anomaly and a bulk theory with an anomaly can fit together, with each solving the other’s problems. Curiously, the authors did not mention any connection with the quantum Hall effect, which had been discovered five years earlier, and I didn’t appreciate the connection myself until years later.

Topological insulators

In the case of topological insulators, the symmetries which protect the gapless edge excitations are time-reversal invariance and conserved particle number, i.e. U(1) symmetry. Though the particle number might not be coupled to an electromagnetic gauge field, it is instructive for the purpose of understanding the properties of the symmetry-protected phase to imagine that the U(1) symmetry is gauged, and then to consider the potential anomalies that could afflict this gauge symmetry. The first topological insulators conceived by theorists were envisioned as systems of non-interacting electrons whose properties were relatively easy to understand using band theory. But it was not so clear at first how interactions among the electrons might alter their exotic behavior. The wonderful thing about anomalies is that they are robust with respect to interactions. In many cases we can infer the features of anomalies by studying a theory of non-interacting particles, assured that these features survive even when the particles interact.

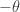As have many previous authors, Metlitski et al. argue that when we couple the conserved particle number to a U(1) gauge field, the effective theory describing the bulk physics of a topological insulator in three dimensions may contain a \theta term. But wait … since the electric field is even under time reversal and the magnetic field is odd, the \theta term is T-odd; under T, \theta is mapped to -\theta, so T seems to be violated if \theta has any nonzero value. Except … we have to remember that \theta is really a periodic variable. 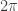For a fermionic topological insulator the period is 2\pi; therefore the theory with 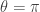\theta = \pi is time reversal invariant; 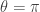\theta = \pi maps to \theta = -\pi under T, which is equivalent to a rotation of \theta by 2\pi. 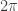For a bosonic topological insulator the period is 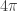4\pi, which means that 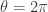\theta = 2\pi is the nontrivial T-invariant value.

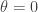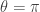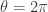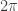If we say that a “trivial” insulator (e.g., the vacuum) has \theta = 0, then we may say that a bulk material with \theta = \pi (fermionic case) or \theta = 2\pi (bosonic case) is a “nontrivial” (a.k.a. topological) insulator. At the edge of the sample, where bulk material meets vacuum, \theta must rotate suddenly by \pi (fermions) or by 2\pi (bosons). The exotic edge physics is a consequence of this abrupt change in \theta.

Monopoles in Flatland

To understand the edge physics, and in particular to grasp how fermionic and bosonic topological insulators differ, Metlitski et al. invite us to imagine a magnetic monopole with magnetic charge g_D passing through the boundary between the bulk and the surrounding vacuum. To the Flatlanders confined to the surface of the bulk sample, the passing monopole induces a sudden change in the magnetic flux through the surface by a single flux quantum g_D, which could arise due to a quantum tunneling event. What does the Flatlander see?

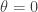In a fermionic topological insulator, there is a monopole that carries charge e/2 when inside the sample (where \theta=-\pi) and charge 0 when outside (where \theta=0). Since electric charge is surely conserved in the full three-dimensional theory, the change in the monopole’s charge must be compensated by a corresponding change in the charge residing on the surface. Flatlanders are puzzled to witness a spontaneously arising excitation with charge e/2. This is an anomaly — electric charge conservation is violated, which can only make sense if Flatlanders are confined to a surface in a higher-dimensional world. Though unable to escape their surface world, the Flatlanders can be convinced by the Monopole that an extra dimension must exist.

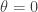In a bosonic topological insulator, the story is somewhat different: there is a monopole that carries electric charge 0 when inside the sample (where \theta=-2\pi) and charge –e when outside (where \theta=0). In this case, though, there are bosonic charge-e particles living on the surface. A monopole can pick up a charged particle as it passes through Flatland, so that its charge is 0 both inside the bulk sample and outside in the vacuum. Flatlanders are happy — electric charge is conserved!

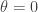But hold on … there’s still something wrong. Inside the bulk (where \theta= -2\pi) a monopole with electric charge 0 is a fermion, while outside in the vacuum (where \theta = 0) it is a boson. In the three-dimensional theory it is not possible for any local process to create an isolated fermion, so if the fermionic monopole becomes a bosonic monople as it passes through Flatland, it must leave a fermion behind. Flatlanders are puzzled to witness a spontaneously arising fermion. This is an anomaly — conservation of fermionic parity is violated, which can only make sense if Flatlanders are confined to a surface in a higher-dimensional world. Once again, the clever residents of Flatland learn from the Monopole about an extra spatial dimension, without ever venturing outside their two-dimensional home.

Topological order gets edgy

This post is already pretty long and I should wrap it up. Before concluding I’ll remark that the theory of symmetry-protected phases has been developing rapidly in recent months.

In particular, a new idea, introduced last fall by Vishwanath and Senthil, has been attracting increasing attention. While in most previously studied SPT phases the unbroken symmetry protects gapless excitations confined to the edge of the sample, Vishwanath and Senthil pointed out another possibility — a gapped edge exhibiting topological order. The surface can support anyons with exotic braiding statistics.

Here, too, anomalies are central to the discussion. While anyons in two-dimensional media are already a much-studied subject, the anyon models that can be realized at the edges of three-dimensional SPT phases are different than anyon models realized in really, truly two-dimensional systems. What’s new are not the braiding properties of the anyons, but rather how the anyons transform under the symmetry. Flatlanders who study the symmetry realization in their gapped two-dimensional world should be able to infer the existence of the three-dimensional bulk.

The pace of discovery picked up this month when four papers appeared simultaneously on the preprint arXiv, by Metlitski-Kane-Fisher, Chen-Fidkowski-Vishwanath, Bonderson-Nayak-Qi, and Wang-Potter-Senthil, all proposing and analyzing models of SPT phases with gapped edges. It remains to be seen, though, whether this physics will be realized in actual materials.

Are we on the edge?

In Flatland, our two-dimensional friend, finally able to perceive the third dimension thanks to the Sphere’s insistent tutelage, begs to enter a world of still higher dimensions, “where thine own intestines, and those of kindred Spheres, will lie exposed to … view.” The Sphere is baffled by the Flatlander’s request, protesting, “There is no such land. The very idea of it is utterly inconceivable.”

Let’s not be so dogmatic as the Sphere. The lessons learned from the quantum Hall effect and the topological insulator have prepared us to take the next step, envisioning our own three-dimensional world as the edge of a higher-dimensional bulk system. The existence of an unseen bulk may be inferred in the future by us edgelings, if experimental explorations of our three-dimensional effective theory reveal anomalies begging for an explanation.

Perhaps we are on the edge … of a great discovery. At least it’s conceivable.

*Disclaimer: The gender politics of Flatland, to put it mildly, is outdated and offensive. I don’t wish to endorse the idea that women are one dimensional! I included the reference to Flatland because the imagery of two-dimensional beings struggling to imagine the third dimension is a perfect fit to the scientific content of this post.