Quantum braiding: It’s all in (and on) your head.

Posted on May 22, 2016 by Nicole Yunger Halpern

Morning sunlight illuminated John Preskill’s lecture notes about Caltech’s quantum-computation course, Ph 219. I’m TAing (the teaching assistant for) Ph 219. I previewed lecture material one sun-kissed Sunday.

Pasadena sunlight spilled through my window. So did the howling of a dog that’s deepened my appreciation for Billy Collins’s poem “Another reason why I don’t keep a gun in the house.” My desk space warmed up, and I unbuttoned my jacket. I underlined a phrase, braided my hair so my neck could cool, and flipped a page.

I flipped back. The phrase concerned a mathematical statement called the Yang-Baxter relation. A sunbeam had winked on in my mind: The Yang-Baxter relation described my hair.

The Yang-Baxter relation belongs to a branch of math called topology. Topology resembles geometry in its focus on shapes. Topologists study spheres, doughnuts, knots, and braids.

Topology describes some quantum physics. Scientists are harnessing this physics to build quantum computers. Alexei Kitaev largely dreamed up the harness. Alexei, a Caltech professor, is teaching Ph 219 this spring.¹ His computational scheme works like this.

We can encode information in radio signals, in letters printed on a page, in the pursing of one’s lips as one passes a howling dog’s owner, and in quantum particles. Imagine three particles on a tabletop.

Consider pushing the particles around like peas on a dinner plate. You could push peas 1 and 2 until they swapped places. The swap represents a computation, in Alexei’s scheme.²

The diagram below shows how the peas move. Imagine slicing the figure into horizontal strips. Each strip would show one instant in time. Letting time run amounts to following the diagram from bottom to top.

Arrows copied from John Preskill’s lecture notes. Peas added by the author.

Imagine swapping peas 1 and 3.

Humor me with one more swap, an interchange of 2 and 3.

Congratulations! You’ve modeled a significant quantum computation. You’ve also braided particles.

The author models a quantum computation.

Let’s recap: You began with peas 1, 2, and 3. You swapped 1 with 2, then 1 with 3, and then 2 with 3. The peas end up ordered oppositely the way they began—end up ordered as 3, 2, 1.

You could, instead, morph 1-2-3 into 3-2-1 via a different sequence of swaps. That sequence, or braid, appears below.

Congratulations! You’ve begun proving the Yang-Baxter relation. You’ve shown that each braid turns 1-2-3 into 3-2-1.

The relation states also that 1-2-3 is topologically equivalent to 3-2-1: Imagine standing atop pea 2 during the 1-2-3 braiding. You’d see peas 1 and 3 circle around you counterclockwise. You’d see the same circling if you stood atop pea 2 during the 3-2-1 braiding.

That Sunday morning, I looked at John’s swap diagrams. I looked at the hair draped over my left shoulder. I looked at John’s swap diagrams.

“Yang-Baxter relation” might sound, to nonspecialists, like a mouthful of tweed. It might sound like a sneeze in a musty library. But an eight-year-old could grasp half the relation. When I braid my hair, I pass my left hand over the back of my neck. Then, I pass my right hand over. But I could have passed the right hand first, then the left. The braid would have ended the same way. The braidings would look identical to a beetle hiding atop what had begun as the middle hunk of hair.

The Yang-Baxter relation.

I tried to keep reading John’s lecture notes, but the analogy mushroomed. Imagine spinning one pea atop the table.

A 360° rotation returns the pea to its initial orientation. You can’t distinguish the pea’s final state from its first. But a quantum particle’s state can change during a 360° rotation. Physicists illustrate such rotations with corkscrews.

A quantum corkscrew (“twisted worldribbon,” in technical jargon)

Like the corkscrews formed as I twirled my hair around a finger. I hadn’t realized that I was fidgeting till I found John’s analysis.

I gave up on his lecture notes as the analogy sprouted legs.

I’ve never mastered the fishtail braid. What computation might it represent? What about the French braid? You begin French-braiding by selecting a clump of hair. You add strands to the clump while braiding. The addition brings to mind particles created (and annihilated) during a topological quantum computation.

Ancient Greek statues wear elaborate hairstyles, replete with braids and twists. Could you decode a Greek hairdo? Might it represent the first 18 digits in pi? How long an algorithm could you run on Rapunzel’s hair?

Call me one bobby pin short of a bun. But shouldn’t a scientist find inspiration in every fiber of nature? The sunlight spilling through a window illuminates no less than the hair spilling over a shoulder. What grows on a quantum physicist’s head informs what grows in it.

¹Alexei and John trade off on teaching Ph 219. Alexei recommends the notes that John wrote while teaching in previous years.

²When your mother ordered you to quit playing with your food, you could have objected, “I’m modeling computations!”

little by little and gate by gate

Posted on April 3, 2016 by Nicole Yunger Halpern

Washington state was drizzling on me. I was dashing from a shuttle to Building 112 on Microsoft’s campus. Microsoft has headquarters near Seattle. The state’s fir trees refreshed me. The campus’s vastness awed me. The conversations planned for the day enthused me. The drizzle dampened me.

Building 112 houses QuArC, one of Microsoft’s research teams. “QuArC” stands for “Quantum Architectures and Computation.” Team members develop quantum algorithms and codes. QuArC members write, as their leader Dr. Krysta Svore says, “software for computers that don’t exist.”

Small quantum computers exist. Large ones have eluded us like gold at the end of a Washington rainbow. Large quantum computers could revolutionize cybersecurity, materials engineering, and fundamental physics. Quantum computers are growing, in labs across the world. When they mature, the computers will need software.

Software consists of instructions. Computers follow instructions as we do. Suppose you want to find and read the poem “anyone lived in a pretty how town,” by 20th-century American poet e e cummings. You follow steps—for example:

1) Wake up your computer.
2) Type your password.
3) Hit “Enter.”
4) Kick yourself for entering the wrong password.
5) Type the right password.
6) Hit “Enter.”
7) Open a web browser.
8) Navigate to Google.
9) Type “anyone lived in a pretty how town e e cummings” into the search bar.
10) Hit “Enter.”
11) Click the Academy of American Poets’ link.
12) Exclaim, “Really? April is National Poetry Month?”
13) Read about National Poetry Month for four-and-a-half minutes.
14) Remember that you intended to look up a poem.
15) Return to the Academy of American Poets’ “anyone lived” webpage.
16) Read the poem.

We break tasks into chunks executed sequentially. So do software writers. Microsoft researchers break up tasks intended for quantum computers to perform.

Your computer completes tasks by sending electrons through circuits. Quantum computers will have circuits. A circuit contains wires, which carry information. The wires run through circuit components called gates. Gates manipulate the information in the wires. A gate can, for instance, add the number carried by this wire to the number carried by that wire.

Running a circuit amounts to completing a task, like hunting a poem. Computer engineers break each circuit into wires and gates, as we broke poem-hunting into steps 1-16.¹

Circuits hearten me, because decomposing tasks heartens me. Suppose I demanded that you read a textbook in a week, or create a seminar in a day, or crack a cybersecurity system. You’d gape like a visitor to Washington who’s realized that she’s forgotten her umbrella.

Suppose I demanded instead that you read five pages, or create one Powerpoint slide, or design one element of a quantum circuit. You might gape. But you’d have more hope.² Life looks more manageable when broken into circuit elements.

Circuit decomposition—and life decomposition—brings to mind “anyone lived in a pretty how town.” The poem concerns two characters who revel in everyday events. Laughter, rain, and stars mark their time. The more the characters attune to nature’s rhythm, the more vibrantly they live:³

little by little and was by was

all by all and deep by deep
and more by more they dream their sleep

Those lines play in my mind when a seminar looms, or a trip to Washington coincident with a paper deadline, or a quantum circuit I’ve no idea how to parse. Break down the task, I tell myself. Inch by inch, we advance. Little by little and drop by drop, step by step and gate by gate.

Not what e e cummings imagined when composing “anyone lived in a pretty how town”

Unless you’re dashing through raindrops to gate designers at Microsoft. I don’t recommend inching through Washington’s rain. But I would have dashed in a drought. What sees us through everyday struggles—the inching of science—if not enthusiasm? We tackle circuits and struggles because, beyond the drizzle, lie ideas and conversations that energize us to run.

e e cummings

With thanks to QuArC members for their time and hospitality.

¹One might object that Steps 4 and 14 don’t belong in the instructions. But software involves error correction.

²Of course you can design a quantum-circuit element. Anyone can quantum.

³Even after the characters die.

March madness and quantum memory

Posted on March 13, 2016 by Nicole Yunger Halpern

Madness seized me this March. It pounced before newspaper and Facebook feeds began buzzing about basketball.¹ I haven’t bought tickets or bet on teams. I don’t obsess over jump-shot statistics. But madness infected me two weeks ago. I began talking with condensed-matter physicists.

Condensed-matter physicists study collections of many particles. Example collections include magnets and crystals. And the semiconductors in the iPhones that report NCAA updates.

Caltech professor Gil Refael studies condensed matter. He specializes in many-body localization. By “many-body,” I mean “involving lots of quantum particles.” By “localization,” I mean “each particle anchors itself to one spot.” We’d expect these particles to spread out, like the eau de hotdog that wafts across a basketball court. But Gil’s particles stay put.

How many-body-localized particles don’t behave.

Experts call many-body localization “MBL.” I’ve accidentally been calling many-body localization “MLB.” Hence the madness. You try injecting baseball into quantum discussions without sounding one out short of an inning.²

I wouldn’t have minded if the madness had erupted in October. The World Series began in October. The World Series involves Major League Baseball, what normal people call “the MLB.” The MLB dominates October; the NCAA dominates March. Preoccupation with the MLB during basketball season embarrasses me. I feel like I’ve bet on the last team that I could remember winning the championship, then realized that that team had last won in 2002.

March madness has been infecting my thoughts about many-body localization. I keep envisioning a localized particle as dribbling a basketball in place, opponents circling, fans screaming, “Go for it!” Then I recall that I’m pondering MBL…I mean, MLB…or the other way around. The dribbler gives way to a baseball player who refuses to abandon first base for second. Then I recall that I should be pondering particles, not playbooks.

Localized particles.

Recollection holds the key to MBL’s importance. Colleagues of Gil’s want to build quantum computers. Computers store information in memories. Memories must retain their contents; information mustn’t dribble away.

Consider recording halftime scores. You could encode the scores in the locations of the particles that form eau de hotdog. (Imagine you have advanced technology that manipulates scent particles.) If Duke had scored one point, you’d put this particle here; if Florida had scored two, you’d put that particle there. The particles—as smells too often do—would drift. You’d lose the information you’d encoded. Better to paint the scores onto scorecards. Dry paint stays put, preserving information.

The quantum particles studied by Gil stay put. They inspire scientists who develop memories for quantum computers. Quantum computation is gunning for a Most Valuable Player plaque in the technology hall of fame. Many-body localized systems could contain Most Valuable Particles.

Remembering the past, some say, one can help one read the future. I don’t memorize teams’ records. I can’t advise you about whom root for. But prospects for quantum memories are brightening. Bet on quantum information science.

¹Non-American readers: University basketball teams compete in a tournament each March. The National Collegiate Athletic Association (NCAA) hosts the tournament. Fans glue themselves to TVs, tweet exaltations and frustrations, and excommunicate friends who support opposing teams.

²Without being John Preskill.

Carbon copy

Posted on February 23, 2016 by benphysics

The anticipatory excitement of summer vacation endures in the teaching profession like no place outside childhood schooldays. Undoubtedly, ranking high on the list that keep teachers teaching. The excitement was high as the summer of 2015 started out the same as it had the three previous years at Caltech. I would show up, find a place to set up, and wait for orders from scientist David Boyd. Upon arrival in Dr. Yeh’s lab, surprisingly, I found all the equipment and my work space very much untouched from last year. I was happy to find it this way, because it likely meant I could continue exactly where I left off last summer. Later, I realized David’s time since I left was devoted to the development of a revolutionary new process for making graphene in large sheets at low temperatures. He did not have time to mess with my stuff, including the stepper-motor I had been working on last summer.

So, I place my glorified man purse in a bottom drawer, log into my computer, and wait. After maybe a half hour I hear the footsteps set to a rhythm defined only by someone with purpose, and I’m sure it’s David. He peeks in the little office where I’m seated and with a brief welcoming phrase informs me that the goal for the summer is to wrap graphene around a thin copper wire using, what he refers to as, “your motor.” The motor is a stepper motor from an experiment David ran several years back. I wired and set up the track and motor last year for a proposed experiment that was never realized involving the growth of graphene strips. Due to the limited time I spend each summer at Caltech (8 weeks), that experiment came to a halt when I left, and was to be continued this year. Instead, the focus veered from growing graphene strips to growing a two to three layer coating of graphene around a copper wire. The procedure remains the same, however, the substrate onto which the graphene grows changes. When growing graphene-strips the substrate is a 25 micron thick copper foil, and after growth the graphene needs to be removed from the copper substrate. In our experiment we used a copper wire with an average thickness of 154 microns, and since the goal is to acquire a copper wire with graphene wrapped around, there’s no need to remove the graphene.

Noteworthy of mention is the great effort toward research concerning the removal and transfer of graphene from copper to more useful substrates. After graphene growth, the challenge shifts to separating the graphene sheet from the copper substrate without damaging the graphene. Next, the graphene is transferred to various substrates for fabrication and other purposes. Current techniques to remove graphene from copper often damage the graphene, ill-effecting the amazing electrical properties warranting great attention from R&D groups globally. A surprisingly simple new technique employs water to harmlessly remove graphene from copper. This technique has been shown to be effective on plasma-enhanced chemical vapor deposition (PECVD). PECVD is the technique employed by scientist David Boyd, and is the focus of his paper published in Nature Communications in March of 2015.

So, David wants me to do something that has never been done before; grow graphene around a copper wire using a translation stage. The technique is to attach an Evenson cavity to the stage of a stepper motor/threaded rod apparatus, and very slowly move the plasma along a strip of copper wire. If successful, this could have far reaching implications for use with copper wire including, but certainly not limited to, corrosion prevention and thermal dissipation due to the high thermal conductivity exhibited by graphene. With David granting me free reign in his lab, and Ph.D. candidate Chen-Chih Hsu agreeing to help, I felt I had all the tools to give it a go.

Setting up this experiment is similar to growing graphene on copper foil using PECVD with a couple modifications. First, prior to pumping the quartz tube down to a near vacuum, we place a single copper wire into the tube instead of thin copper foil. Also, special care is taken when setting up the translation stage ensuring the Evenson cavity, attached to the stage, travels perfectly parallel to the quartz tube so as not to create a bind between the cavity and tube during travel. For the first trial we decide to grow along a 5cm long section of copper wire at a translation speed of 25 microns per second, which is a very slow speed made possible by the use of the stepper motor apparatus. Per usual, after growth we check the sample using Raman Spectroscopy. The graph shown here is the actual Raman taken in the lab immediately after growth. As the sample is scanned, the graph develops from right to left. We’re not expecting to see anything of much interest, however, hope and excitement steadily rise as the computer monitor shows a well defined 2D-peak (right peak), a G-peak (middle peak), and a D-peak (left peak) with a height indicative of high defects. Not the greatest of Raman spectra if we were shooting for defect-free monolayer graphene, but this is a very strong indication that we have 2-3 layer graphene on the copper wire. How could this be? Chen-Chih and I looked at each other incredulously. We quickly checked several locations along the wire and found the same result. We did it! Not only did we do it, but we did it on our first try! OK, now we can party. Streamers popped up into the air, a DJ with a turn table slid out from one of the walls, a perfectly synchronized kick line of cabaret dancers pranced about…… okay, back to reality, we had a high-five and a back-and-forth “wow, that’s so cool!”

We knew before we even reported our success to David, and eventually Professor Yeh, that they would both, immediately, ask for the exact parameters of the experiment and if the results were reproducible. So, we set off to try and grow again. Unfortunately, the second run did not yield a copper wire coated with graphene. The third trial did not yield graphene, and neither did the fourth or fifth. We were, however, finding that multi-layer graphene was growing at the tips of the copper wire, but not in the middle sections. Our hypothesis at that point was that the existence of three edges at the tips of the wire aided the growth of graphene, compared to only two edges in the wire’s midsection (we are still not sure if this is the whole story).

In an effort to repeat the experiment and attain the parameters for growth, an issue with the experimental setup needed to be addressed. We lacked control concerning the exact mixture of each gas employed for CVD (Chemical Vapor Deposition). In the initial setup of the experiment, a lack of control was acceptable, because the goal was only to discover if growing graphene around a copper wire was possible. Now that we knew it was possible, attaining reproducible results required a deeper understanding of the process, therefore, more precise control in our setup. Dr. Boyd agreed, and ordered two leak valves, providing greater control over the exact recipe for the mixture of gases used for CVD. With this improved control, the hope is to be able to control and, therefore, detect the exact gas mixture yielding the much needed parameters for reliable graphene growth on a copper wire.

Unfortunately, my last day at Caltech before returning to my regular teaching gig, and the delivery of the leak valves occurred on the same day. Fortunately, I will be returning this summer (2016) to continue the search for the elusive parameters. If we succeed, David Boyd’s and Chen-Chih’s names will, once again, show up in a prestigious journal (Nature, Science, one of those…) and, just maybe, mine will make it there too. For the first time ever.

Quantum Information: Episode II: The Tools’ Applications

Posted on December 27, 2015 by Nicole Yunger Halpern

Monday dawns. Headlines report that “Star Wars: Episode VII” has earned more money, during its opening weekend, than I hope to earn in my lifetime. Trading the newspaper for my laptop, I learn that a friend has discovered ThinkGeek’s BB-8 plushie. “I want one!” she exclaims in a Facebook post. “Because BB-8 definitely needs to be hugged.”

BB-8 plays sidekick to Star Wars hero Poe Dameron. The droid has a spherical body covered with metallic panels and lights.Mr. Gadget and Frosty the Snowman could have spawned such offspring. BB-8 has captured viewers’ hearts, and its chirps have captured cell-phone ringtones.

ThinkGeek’s BB-8 plushie

Still, I scratch my head over my friend’s Facebook post. Hugged? Why would she hug…

Oh. Oops.

I’ve mentally verbalized “BB-8” as “BB84.” BB84 denotes an application of quantum theory to cryptography. Cryptographers safeguard information from eavesdroppers and tampering. I’ve been thinking that my friend wants to hug a safety protocol.

Charles Bennett and Gilles Brassard invented BB84 in 1984. Imagine wanting to tell someone a secret. Suppose I wish to coordinate, with a classmate, the purchase of a BB-8 plushie for our friend the droid-hugger. Suppose that the classmate and I can communicate only via a public channel on which the droid-hugger eavesdrops.

Cryptographers advise me to send my classmate a key. A key is a random string of letters, such as CCCAAACCABACA. I’ll encode my message with the string, with which my classmate will decode the message.

I have to transmit the key via the public channel. But the droid-hugger eavesdrops on the public channel. Haven’t we taken one step forward and one step back? Why would the key secure our information?

Because quantum-information science enables me to to transmit the key without the droid-hugger’s obtaining it. I won’t transmit random letters; I’ll transmit quantum states. That is, I’ll transmit physical systems, such as photons (particles of light), whose properties encode quantum information.

A nonquantum letter has a value, such as A or B or C. Each letter has one and only one value, regardless of whether anyone knows what value the letter has. You can learn the value by measuring (looking at) the letter. We can’t necessarily associate such a value with a quantum state. Imagine my classmate measuring a state I send. Which value the measurement device outputs depends on chance and on how my classmate looks at the state.

If the droid-hugger intercepts and measures the state, she’ll change it. My classmate and I will notice such changes. We’ll scrap our key and repeat the BB84 protocol until the droid-hugger quits eavesdropping.

BB84 launched quantum cryptography, the safeguarding of information with quantum physics. Today’s quantum cryptographers rely on BB84 as you rely, when planning a holiday feast, on a carrot-cake recipe that passed your brother’s taste test on his birthday. Quantum cryptographers construct protocols dependent on lines like “The message sender and receiver are assumed to share a key distributed, e.g., via the BB84 protocol.”

BB84 has become a primitive task, a solved problem whose results we invoke in more-complicated problems. Other quantum-information primitives include (warning: jargon ahead) entanglement distillation, entanglement dilution, quantum data compression, and quantum-state merging. Quantum-information scientists solved many primitive problems during the 1990s and early 2000s. You can apply those primitives, even if you’ve forgotten how to prove them.

A primitive task, like quantum-entanglement distillation

Those primitives appear to darken quantum information’s horizons. The spring before I started my PhD, an older physicist asked me why I was specializing in quantum information theory. Haven’t all the problems been solved? he asked. Isn’t quantum information theory “dead”?

Imagine discovering how to power plasma blades with kyber crystals. Would you declare, “Problem solved” and relegate your blades to the attic? Or would you apply your tool to defending freedom?

Primitive quantum-information tools are unknotting problems throughout physics—in computer science; chemistry; optics (the study of light); thermodynamics (the study of work, heat, and efficiency); and string theory. My advisor has tracked how uses of “entanglement,” a quantum-information term, have swelled in high-energy-physics papers.

A colleague of that older physicist views quantum information theory as a toolkit, a perspective, a lens through which to view science. During the 1700s, the calculus invented by Isaac Newton and Gottfried Leibniz revolutionized physics. Emmy Noether (1882—1935) recast physics in terms of symmetries and conservation laws. (If the forces acting on a system don’t change in time, for example, the system doesn’t gain or lose energy. A constant force is invariant under, or symmetric with respect to, the progression of time. This symmetry implies that the system’s energy is conserved.) We can cast physics instead (jargon ahead) in terms of the minimization of a free energy or an action.

Quantum information theory, this physicist predicted, will revolutionize physics as calculus, symmetries, conservation, and free energy have. Quantum-information tools such as entropies, entanglement, and qubits will bleed into subfields of physics as Lucasfilm has bled into the fanfiction, LEGO, and Halloween-costume markets.

BB84, and the solution of other primitives, have not killed quantum information. They’ve empowered it to spread—thankfully, to this early-career quantum information scientist. Never mind BB-8; I’d rather hug BB84. Perhaps I shall. Engineers have realized technologies that debuted on Star Trek; quantum mechanics has secured key sharing; bakers have crafted cakes shaped like the Internet; and a droid’s popularity rivals R2D2’s. Maybe next Monday will bring a BB84 plushie.

The author hugging the BB84 paper and a plushie. On my wish list: a combination of the two.

Wouldn’t you like to know what’s going on in my mind?

Posted on November 6, 2015 by preskill

I suppose most theoretical physicists who (like me) are comfortably past the age of 60 worry about their susceptibility to “crazy-old-guy syndrome.” (Sorry for the sexism, but all the victims of this malady I know are guys.) It can be sad when a formerly great scientist falls far out of the mainstream and seems to be spouting nonsense.

Matthew Fisher is only 55, but reluctance to be seen as a crazy old guy might partially explain why he has kept pretty quiet about his passionate pursuit of neuroscience over the past three years. That changed two months ago when he posted a paper on the arXiv about Quantum Cognition.

Neuroscience has a very seductive pull, because it is at once very accessible and very inaccessible. While a theoretical physicist might think and write about a brane even without having or seeing a brane, everybody’s got a brain (some scarecrows excepted). On the other hand, while it’s not too hard to write down and study the equations that describe a brane, it is not at all easy to write down the equations for a brain, let alone solve them. The brain is fascinating because we know so little about it. And … how can anyone with a healthy appreciation for Gödel’s Theorem not be intrigued by the very idea of a brain that thinks about itself?

(Almost) everybody’s got a brain.

The idea that quantum effects could have an important role in brain function is not new, but is routinely dismissed as wildly implausible. Matthew Fisher begs to differ. And those who read his paper (as I hope many will) are bound to conclude: This old guy’s not so crazy. He may be onto something. At least he’s raising some very interesting questions.

My appreciation for Matthew and his paper was heightened further this Wednesday, when Matthew stopped by Caltech for a lunch-time seminar and one of my interminable dinner-time group meetings. I don’t know whether my brain is performing quantum information processing (and neither does Matthew), but just the thought that it might be is lighting me up like a zebrafish.

Following Matthew, let’s take a deep breath and ask ourselves: What would need to be true for quantum information processing to be important in the brain? Presumably we would need ways to (1) store quantum information for a long time, (2) transport quantum information, (3) create entanglement, and (4) have entanglement influence the firing of neurons. After a three-year quest, Matthew has interesting things to say about all of these issues. For details, you should read the paper.

Matthew argues that the only plausible repositories for quantum information in the brain are the Phosphorus-31 nuclear spins in phosphate ions. Because these nuclei are spin-1/2, they have no electric quadrupole moments and hence corresponding long coherence times — of order a second. That may not be long enough, but phosphate ions can be bound with calcium ions into objects called Posner clusters, each containing six P-31 nuclei. The phosphorus nuclei in Posner clusters might have coherence times greatly enhanced by motional narrowing, perhaps as long as weeks or even longer.

Where energy is being consumed in a cell, ATP sometimes releases diphosphate ions (what biochemists call pyrophosphate), which are later broken into two separate phosphate ions, each with a single P-31 qubit. Matthew argues that the breakup of the diphosphate, catalyzed by a suitable enzyme, will occur at an enhanced rate when these two P-31 qubits are in a spin singlet rather than a spin triplet. The reason is that the enzyme has to grab ahold of the diphosphate molecule and stop its rotation in order to break it apart, which is much easier when the molecule has even rather than odd orbital angular momentum; therefore due to Fermi statistics the spin state of the P-31 nuclei must be antisymmetric. Thus wherever ATP is consumed there is a plentiful source of entangled qubit pairs.

If the phosphate molecules remain unbound, this entanglement will decay in about a second, but it is a different story if the phosphate ions group together quickly enough into Posner clusters, allowing the entanglement to survive for a much longer time. If the two members of an entangled qubit pair are snatched up by different Posner clusters, the clusters may then be transported into different cells, distributing the entanglement over relatively long distances.

(a) Two entangled Posner clusters. Each dot is a P-31 nuclear spin, and each dashed line represents a singlet pair. (b) Many entangled Posner clusters. [From Fisher 2015]

What causes a neuron to fire is a complicated story that I won’t attempt to wade into. Suffice it to say that part of the story may involve the chemical binding of a pair of Posner clusters which then melt if the environment is sufficiently acidic, releasing calcium ions and phosphate ions which enhance the firing. The melting rate depends on the spin state of the six P-31 nuclei within the cluster, so that entanglement between clusters in different cells may induce nonlocal correlations among different neurons, which could be quite complex if entanglement is widely distributed.

This scenario raises more questions than it answers, but these are definitely scientific questions inviting further investigation and experimental exploration. One thing that is far from clear at this stage is whether such quantum correlations among neurons (if they exist at all) would be easy to simulate with a classical computer. Even if that turns out to be so, these potential quantum effects involving many neurons could be fabulously interesting. IQIM’s mission is to reach for transformative quantum science, particularly approaches that take advantage of synergies between different fields of study. This topic certainly qualifies.* It’s going to be great fun to see where it leads.

If you are a young and ambitious scientist, you may be contemplating the dilemma: Should I pursue quantum physics or neuroscience? Maybe, just maybe, the right answer is: Both.

*Matthew is the only member of the IQIM faculty who is not a Caltech professor, though he once was.

Toward physical realizations of thermodynamic resource theories

Posted on September 13, 2015 by Nicole Yunger Halpern

“This is your arch-nemesis.”

The thank-you slide of my presentation remained onscreen, and the question-and-answer session had begun. I was presenting a seminar about thermodynamic resource theories (TRTs), models developed by quantum-information theorists for small-scale exchanges of heat and work. The audience consisted of condensed-matter physicists who studied graphene and photonic crystals. I was beginning to regret my topic’s abstractness.

The question-asker pointed at a listener.

“This is an experimentalist,” he continued, “your arch-nemesis. What implications does your theory have for his lab? Does it have any? Why should he care?”

I could have answered better. I apologized that quantum-information theorists, reared on the rarefied air of Dirac bras and kets, had developed TRTs. I recalled the baby steps with which science sometimes migrates from theory to experiment. I could have advocated for bounding, with idealizations, efficiencies achievable in labs. I should have invoked the connections being developed with fluctuation results, statistical mechanical theorems that have withstood experimental tests.

The crowd looked unconvinced, but I scored one point: The experimentalist was not my arch-nemesis.

“My new friend,” I corrected the questioner.

His question has burned in my mind for two years. Experiments have inspired, but not guided, TRTs. TRTs have yet to drive experiments. Can we strengthen the connection between TRTs and the natural world? If so, what tools must resource theorists develop to predict outcomes of experiments? If not, are resource theorists doing physics?

http://everystevejobsvideo.com/steve-jobs-qa-session-excerpt-following-antennagate-2010/

A Q&A more successful than mine.

I explore answers to these questions in a paper released today. Ian Durham and Dean Rickles were kind enough to request a contribution for a book of conference proceedings. The conference, “Information and Interaction: Eddington, Wheeler, and the Limits of Knowledge” took place at the University of Cambridge (including a graveyard thereof), thanks to FQXi (the Foundational Questions Institute).

What, I asked my advisor, does one write for conference proceedings?

“Proceedings are a great opportunity to get something off your chest,” John said.

That seminar Q&A had sat on my chest, like a pet cat who half-smothers you while you’re sleeping, for two years. Theorists often justify TRTs with experiments.^* Experimentalists, an argument goes, are probing limits of physics. Conventional statistical mechanics describe these regimes poorly. To understand these experiments, and to apply them to technologies, we must explore TRTs.

Does that argument not merit testing? If experimentalists observe the extremes predicted with TRTs, then the justifications for, and the timeliness of, TRT research will grow.

http://maryqin.com/wp-content/uploads/2014/05/

Something to get off your chest. Like the contents of a conference-proceedings paper, according to my advisor.

You’ve read the paper’s introduction, the first eight paragraphs of this blog post. (Who wouldn’t want to begin a paper with a mortifying anecdote?) Later in the paper, I introduce TRTs and their role in one-shot statistical mechanics, the analysis of work, heat, and entropies on small scales. I discuss whether TRTs can be realized and whether physicists should care. I identify eleven opportunities for shifting TRTs toward experiments. Three opportunities concern what merits realizing and how, in principle, we can realize it. Six adjustments to TRTs could improve TRTs’ realism. Two more-out-there opportunities, though less critical to realizations, could diversify the platforms with which we might realize TRTs.

One opportunity is the physical realization of thermal embezzlement. TRTs, like thermodynamic laws, dictate how systems can and cannot evolve. Suppose that a state $R$ cannot transform into a state $S$ : $R \not\mapsto S$ . An ancilla $C$ , called a catalyst, might facilitate the transformation: $R + C \mapsto S + C$ . Catalysts act like engines used to extract work from a pair of heat baths.

Engines degrade, so a realistic transformation might yield $S + \tilde{C}$ , wherein $\tilde{C}$ resembles $C$ . For certain definitions of “resembles,”** TRTs imply, one can extract arbitrary amounts of work by negligibly degrading $C$ . Detecting the degradation—the work extraction’s cost—is difficult. Extracting arbitrary amounts of work at a difficult-to-detect cost contradicts the spirit of thermodynamic law.

The spirit, not the letter. Embezzlement seems physically realizable, in principle. Detecting embezzlement could push experimentalists’ abilities to distinguish between close-together states $C$ and $\tilde{C}$ . I hope that that challenge, and the chance to violate the spirit of thermodynamic law, attracts researchers. Alternatively, theorists could redefine “resembles” so that $C$ doesn’t rub the law the wrong way.

The paper’s broadness evokes a caveat of Arthur Eddington’s. In 1927, Eddington presented Gifford Lectures entitled The Nature of the Physical World. Being a physicist, he admitted, “I have much to fear from the expert philosophical critic.” Specializing in TRTs, I have much to fear from the expert experimental critic. The paper is intended to point out, and to initiate responses to, the lack of physical realizations of TRTs. Some concerns are practical; some, philosophical. I expect and hope that the discussion will continue…preferably with more cooperation and charity than during that Q&A.

If you want to continue the discussion, drop me a line.

^*So do theorists-in-training. I have.

**A definition that involves the trace distance.

Bits, bears, and beyond in Banff

Posted on August 2, 2015 by Nicole Yunger Halpern

Another conference about entropy. Another graveyard.

Last year, I blogged about the University of Cambridge cemetery visited by participants in the conference “Eddington and Wheeler: Information and Interaction.” We’d lectured each other about entropy–a quantification of decay, of the march of time. Then we marched to an overgrown graveyard, where scientists who’d lectured about entropy decades earlier were decaying.

This July, I attended the conference “Beyond i.i.d. in information theory.” The acronym “i.i.d.” stands for “independent and identically distributed,” which requires its own explanation. The conference took place at BIRS, the Banff International Research Station, in Canada. Locals pronounce “BIRS” as “burrs,” the spiky plant bits that stick to your socks when you hike. (I had thought that one pronounces “BIRS” as “beers,” over which participants in quantum conferences debate about the Measurement Problem.) Conversations at “Beyond i.i.d.” dinner tables ranged from mathematical identities to the hiking for which most tourists visit Banff to the bears we’d been advised to avoid while hiking. So let me explain the meaning of “i.i.d.” in terms of bear attacks.

The BIRS conference center. Beyond here, there be bears.

Suppose that, every day, exactly one bear attacks you as you hike in Banff. Every day, you have a probability p₁ of facing down a black bear, a probability p₂ of facing down a grizzly, and so on. These probabilities form a distribution {p_i} over the set of possible events (of possible attacks). We call the type of attack that occurs on a given day a random variable. The distribution associated with each day equals the distribution associated with each other day. Hence the variables are identically distributed. The Monday distribution doesn’t affect the Tuesday distribution and so on, so the distributions are independent.

Information theorists quantify efficiencies with which i.i.d. tasks can be performed. Suppose that your mother expresses concern about your hiking. She asks you to report which bear harassed you on which day. You compress your report into the fewest possible bits, or units of information. Consider the limit as the number of days approaches infinity, called the asymptotic limit. The number of bits required per day approaches a function, called the Shannon entropy H_S, of the distribution:

Number of bits required per day → H_S({p_i}).

The Shannon entropy describes many asymptotic properties of i.i.d. variables. Similarly, the von Neumann entropy H_vN describes many asymptotic properties of i.i.d. quantum states.

But you don’t hike for infinitely many days. The rate of black-bear attacks ebbs and flows. If you stumbled into grizzly land on Friday, you’ll probably avoid it, and have a lower grizzly-attack probability, on Saturday. Into how few bits can you compress a set of nonasymptotic, non-i.i.d. variables?

We answer such questions in terms of ɛ-smooth α-Rényi entropies, the sandwiched Rényi relative entropy, the hypothesis-testing entropy, and related beasts. These beasts form a zoo diagrammed by conference participant Philippe Faist. I wish I had his diagram on a placemat.

“Beyond i.i.d.” participants define these entropies, generalize the entropies, probe the entropies’ properties, and apply the entropies to physics. Want to quantify the efficiency with which you can perform an information-processing task or a thermodynamic task? An entropy might hold the key.

Many highlights distinguished the conference; I’ll mention a handful. If the jargon upsets your stomach, skip three paragraphs to Thermodynamic Thursday.

Aram Harrow introduced a resource theory that resembles entanglement theory but whose agents pay to communicate classically. Why, I interrupted him, define such a theory? The backstory involves a wager against quantum-information pioneer Charlie Bennett (more precisely, against an opinion of Bennett’s). For details, and for a quantum version of The Princess and the Pea, watch Aram’s talk.

Graeme Smith and colleagues “remove[d] the . . . creativity” from proofs that certain entropic quantities satisfy subadditivity. Subadditivity is a property that facilitates proofs and that offers physical insights into applications. Graeme & co. designed an algorithm for checking whether entropic quantity Q satisfies subadditivity. Just add water; no innovation required. How appropriate, conference co-organizer Mark Wilde observed. BIRS has the slogan “Inspiring creativity.”

Patrick Hayden applied one-shot entropies to AdS/CFT and emergent spacetime, enthused about elsewhere on this blog. Debbie Leung discussed approximations to Haar-random unitaries. Gilad Gour compared resource theories.

Conference participants graciously tolerated my talk about thermodynamic resource theories. I closed my eyes to symbolize the ignorance quantified by entropy. Not really; the photo didn’t turn out as well as hoped, despite the photographer’s goodwill. But I could have closed my eyes to symbolize entropic ignorance.

Thermodynamics and resource theories dominated Thursday. Thermodynamics is the physics of heat, work, entropy, and stasis. Resource theories are simple models for transformations, like from a charged battery and a Tesla car at the bottom of a hill to an empty battery and a Tesla atop a hill.

My advisor’s Tesla. No wonder I study thermodynamic resource theories.

Philippe Faist, diagrammer of the Entropy Zoo, compared two models for thermodynamic operations. I introduced a generalization of resource theories for thermodynamics. Last year, Joe Renes of ETH and I broadened thermo resource theories to model exchanges of not only heat, but also particles, angular momentum, and other quantities. We calculated work in terms of the hypothesis-testing entropy. Though our generalization won’t surprise Quantum Frontiers diehards, the magic tricks in my presentation might.

At twilight on Thermodynamic Thursday, I meandered down the mountain from the conference center. Entropies hummed in my mind like the mosquitoes I slapped from my calves. Rising from scratching a bite, I confronted the Banff Cemetery. Half-wild greenery framed the headstones that bordered the gravel path I was following. Thermodynamicists have associated entropy with the passage of time, with deterioration, with a fate we can’t escape. I seem unable to escape from brushing past cemeteries at entropy conferences.

Not that I mind, I thought while scratching the bite in Pasadena. At least I escaped attacks by Banff’s bears.

With thanks to the conference organizers and to BIRS for the opportunity to participate in “Beyond i.i.d. 2015.”

Ant-Man and the Quantum Realm

Posted on July 20, 2015 by spiros

It was the first week of August last summer and I was at LAX for a trip to North Carolina as a guest speaker at Project Scientist’s STEM summer camp for young women. I had booked an early morning flight and had arrived at my gate with time to spare, so I decided to get some breakfast. I walked by a smart-looking salad bar and thought: Today is the day. Moving past the salad bar, I ordered a juicy cheeseburger with fries at the adjacent McDonald’s. Growing up in Greece, eating McDonald’s was a rare treat; as was playing video games with my brothers and reading comic books late at night. Yet, through a weird twist of fate, it was these last two guilty pleasures that were to become my Hadouken!, my Hulk, Smash! of choice for breaking down the barriers between the world of quantum mechanics and the everyday reality of our super-normal, super-predictable lives.

I finished my burger, stuffing the last few delicious fries in my mouth, when my phone buzzed – I had a call from The Science and Entertainment Exchange, a non-profit organization funded by the National Academy of Sciences, whose purpose is to bring leading scientists in contact with Hollywood in order to elevate the level of science in the movies. I was to report to Atlanta, GA for a movie consult on a new superhero movie: Ant-Man. As I listened to the director of the Exchange discuss the assignment, I grumbled to myself: Why can’t I be the guy who works on Thor? Who is this Ant-Man anyways? But, in typical Hollywood fashion, the call had a happy ending: “Paul Rudd is Ant-Man. He may be at the meeting, but I can’t promise anything.” Marvel would cover my expenses, so my reluctant reply went something like this:

Hell yeah.

The meeting was in three days time. I would finish my visit to Queens University in Charlotte, NC and take the next flight out to Atlanta. But first, some fun and games were in order. As part of my visit to Project Scientist’s camp, I was invited to teach quantum mechanics to a group of forty girls, ages 8-12, all of whom were interested in science, engineering and mathematics and many of whom did not have the financial means to pursue these interests outside of the classroom. So, I went to Queens University with several copies of MinecraftEDU, the educational component to one of the most popular video games of all time: Minecraft. As I described in “Can a game teach kids quantum mechanics”, I spent the summer of 2013 designing qCraft, a modification (mod) to Minecraft that allows players to craft blocks imbued with quantum superpowers such as quantum superposition and quantum entanglement. The mod, developed in collaboration with Google and TeachersGaming, became popular, amassing millions of downloads around the world. But it is one thing to look at statistics as a measure of success, and another to look into the eyes of these girls as they lost themselves in a game (qCraft is free to download and comes with an accompanying curriculum) designed to teach them the heady concepts that inspired Richard Feynman to quip: If you think you understand quantum theory, you don’t.

My visit to Charlotte was so wonderful that I nearly decided to cancel my trip to Atlanta in order to stay with the girls and their mentors until the end of the week. But Mr. Rudd deserved the very best science could offer, so I boarded my flight and resolved to bring Project Scientist to Caltech the next summer. On my way to Atlanta, I used the in-flight WiFi to do some research on Ant-Man. He was part of the original Avengers, a founding member, in fact (nice!) His name was Dr. Hank Pym. He had developed a particle, aptly named after himself, which allowed him to shrink the space between atoms (well now…) He embedded vials of that particle in a suit that allowed him to shrink to the size of an ant (of course, that makes sense.) In short, he was a mad, mad scientist. And I was called in to help his successor, Scott Lang (Paul Rudd’s character), navigate his way through the physics of shrinking. Holy guacamole Ant-man! How does one shrink the space between atoms? As James Kakalios, author of The Physics of Superheroes, puts it in a recent article on Nate Silver’s FiveThirtyEight:

We’re made of atoms, and the neighboring atoms are all touching each other. One method of changing your size that’s out: Just squeeze the atoms closer together.
…
So the other option: What determines the size of atoms anyway?
…
We can calculate this with quantum mechanics, and it turns out to be the ratio of fundamental constants: Planck’s constant and the mass of an electron and the charge of the electron and this and that. The thing that all these constants have in common is that they’re constant. They don’t change.

Wonderful. Just peachy. How am I supposed to come up with a way that will allow Ant-Man to shrink to the size of an ant, if one of the top experts in movie science magic thinks that our best bet is to somehow change fundamental constants of nature?

Enter Pinewood Studios

The flight was longer than I expected, which gave me time to think. A limo was waiting for me at the airport; I was to be taken directly to Pinewood Studios, luggage in hand and all. Once I was at my destination, I was escorted to the 3rd floor of a nondescript building, accessible only through special authorization (nice touch, Marvel). I was shown to what seemed like the main conference room, an open area with a large conference table. I expected that I would have to wait an hour before anyone showed up, so I started fiddling with my phone, making myself look busy. The next time I looked up, Paul Rudd was tapping my shoulder, dressed in sweats after what seemed like a training session for The 300.

The Meeting

Within minutes, the director (Peyton Reed), the writers, producers, VFX specialists, computer playback experts (I became friends with their supervisor, Mr. Matthew Morrissey, who went to great lengths to represent the atoms on-screen as clouds of probability, in the s, p, d, f orbital configurations you see flashing in quantum superposition behind Hank Pym at his lab) and everyone else involved with the movie was in the room. I sat at the head of the long table with Paul next to me. He asked most of the questions along with the director, but at the time I didn’t know Paul was involved with writing the script. We discussed a lot of things, but what got everyone excited was when I told them that the laws of physics as we know them may break down as we delve deeper and deeper into the quantum realm. You see, all of the other superheroes, no matter how strong and super, had powers that conformed to the laws of physics (stretching them from time to time, but never breaking them). But if someone could go to a place where the laws of physics as we know them were not yet formed, at a place where the arrow of time was broken and the fabric of space was not yet woven, the powers of such a master of the quantum realm would only be constrained by their ability to come back to the same (or similar) reality from which they departed. All the superheroes of Marvel and DC Comics combined would stand no chance against Ant-Man with a malfunctioning regulator…

The Quantum Realm

The birth of the term itself is an interesting story. Brad Winderbaum, co-producer for the movie, emailed me a couple of days after the meeting with the following request: Could I come up with a term describing Ant-Man going to the “microverse”? The term “microverse” carried legal baggage, so something fresh was needed. I offered “going nano”, “going quantum”, “going atomic”, or… “quantum realm”. I didn’t know how small the “microverse” scale was supposed to be in a writer’s mind (in a physicist’s mind it is exactly 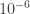$10^{-6}$ meters – one thousandth of a millimeter), hence the many options. The reply was quick:

Thanks Spiros! Quantum Realm is a pretty great term.

Et voilà. Ant-Man was going to the quantum realm, a place where time and space dissolve and the only thing strong enough to anchor Scott Lang to reality is… You have to watch the movie to see what that is – it was an off-the-cuff remark I made at the meeting… At the end of the meeting, Paul, Peyton and the others thanked me and asked me if I could fly to San Francisco the next week for the first week of shooting. There, I would have met Michael Douglas and Evangeline Lilly, but I declined the generous offer. It was the week of Innoworks Academy at Caltech, an award-winning summer camp for middle school kids on the free/reduced lunch program. As the camp’s adviser, I resolved to never miss a camp as long as I was in the country and San Francisco is in the same state as Caltech. My mom would be proud of my decision (I hope), though an autograph from Mr. Douglas would have fetched me a really good hug.

The Movie

I just watched the movie yesterday (it is actually good!) and the feeling was surreal. Because I had no idea what to expect. Because I never thought that the people in that room would take what I was saying seriously enough to use it in the movie. I never got a copy of the script and during the official premiere three weeks ago, I was delivering a lecture on the future of quantum computing in a monastery in Madrid, Spain. When I found out that Kevin Feige, president of Marvel Studios, said this at a recent interview, my heart skipped several beats:

But the truth is, there is so much in Ant-Man: introducing a new hero, introducing a very important part of technology in the Marvel universe, the Pym particles. Ant-Man getting on the Avengers’ radar in this film and even – this is the weirdest part, you shouldn’t really talk about it because it won’t be apparent for years – but the whole notion of the quantum realm and the whole notion of going to places that are so out there, they are almost mind-bendingly hard to fathom. It all plays into Phase Three.

The third phase of the Marvel Cinematic Universe is about to go quantum and all I can think of is: I better start reading comic books again. But first, I have to teach a bunch of 8-12 year-old girls quantum physics through Minecraft. It is, after all, the final week of Project Scientist here at Caltech this summer and the theme is coding. With quantum computers at the near horizon, these young women need to learn how to program Asimov’s laws of quantum robotics into our benevolent quantum A.I. overlords. These young women are humanity’s new hope…

Holography and the MERA

Posted on June 26, 2015 by Aidan Chatwin-Davies

The AdS/MERA correspondence has been making the rounds of the blogosphere with nice posts by Scott Aaronson and Sean Carroll, so let’s take a look at the topic here at Quantum Frontiers.

The question of how to formulate a quantum theory of gravity is a long-standing open problem in theoretical physics. Somewhat recently, an idea that has gained a lot of traction (and that Spiros has blogged about before) is emergence. This is the idea that space and time may emerge from some more fine-grained quantum objects and their interactions. If we could understand how classical spacetime emerges from an underlying quantum system, then it’s not too much of a stretch to hope that this understanding would give us insight into the full quantum nature of spacetime.

One type of emergence is exhibited in holography, which is the idea that certain (D+1)-dimensional systems with gravity are exactly equivalent to D-dimensional quantum theories without gravity. (Note that we’re calling time a dimension here. For example, you would say that on a day-to-day basis we experience D = 4 dimensions.) In this case, that extra +1 dimension and the concomitant gravitational dynamics are emergent phenomena.

A nice aspect of holography is that it is explicitly realized by the AdS/CFT correspondence. This correspondence proposes that a particular class of spacetimes—ones that asymptotically look like anti-de Sitter space, or AdS—are equivalent to states of a particular type of quantum system—a conformal field theory, or CFT. A convenient visualization is to draw the AdS spacetime as a cylinder, where time marches forward as you move up the cylinder and different slices of the cylinder correspond to snapshots of space at different instants of time. Conveniently, in this picture you can think of the corresponding CFT as living on the boundary of the cylinder, which, you should note, has one less dimension than the “bulk” inside the cylinder.

Even within this nice picture of holography that we get from the AdS/CFT correspondence, there is a question of how exactly do CFT, or boundary quantities map onto quantities in the AdS bulk. This is where a certain tool from quantum information theory called tensor networks has recently shown a lot of promise.

A tensor network is a way to efficiently represent certain states of a quantum system. Moreover, they have nice graphical representations which look something like this:

Beni discussed one type of tensor network in his post on holographic codes. In this post, let’s discuss the tensor network shown above, which is known as the Multiscale Entanglement Renormalization Ansatz, or MERA.

The MERA was initially developed by Guifre Vidal and Glen Evenbly as an efficient approximation to the ground state of a CFT. Roughly speaking, in the picture of a MERA above, one starts with a simple state at the centre, and as you move outward through the network, the MERA tells you how to build up a CFT state which lives on the legs at the boundary. The MERA caught the eye of Brian Swingle, who noticed that it looks an awfully lot like a discretization of a slice of the AdS cylinder shown above. As such, it wasn’t a preposterously big leap to suggest a possible “AdS/MERA correspondence.” Namely, perhaps it’s more than a simple coincidence that a MERA both encodes a CFT state and resembles a slice of AdS. Perhaps the MERA gives us the tools that are required to construct a map between the boundary and the bulk!

So, how seriously should one take the possibility of an AdS/MERA correspondence? That’s the question that my colleagues and I addressed in a recent paper. Essentially, there are several properties that a consistent holographic theory should satisfy in both the bulk and the boundary. We asked whether these properties are still simultaneously satisfied in a correspondence where the bulk and boundary are related by a MERA.

What we found was that you invariably run into inconsistencies between bulk and boundary physics, at least in the simplest construals of what an AdS/MERA correspondence might be. This doesn’t mean that there is no hope for an AdS/MERA correspondence. Rather, it says that the simplest approach will not work. For a good correspondence, you would need to augment the MERA with some additional structure, or perhaps consider different tensor networks altogether. For instance, the holographic code features a tensor network which hints at a possible bulk/boundary correspondence, and the consistency conditions that we proposed are a good list of checks for Beni and company as they work out the extent to which the code can describe holographic CFTs. Indeed, a good way to summarize how our work fits into the picture of quantum gravity alongside holography and tensors networks is by saying that it’s nice to have good signposts on the road when you don’t have a map.

Quantum Frontiers

A blog by the Institute for Quantum Information and Matter @ Caltech

Category Archives: Real science

Quantum braiding: It’s all in (and on) your head.

little by little and gate by gate

March madness and quantum memory

Carbon copy

Quantum Information: Episode II: The Tools’ Applications

Wouldn’t you like to know what’s going on in my mind?

Toward physical realizations of thermodynamic resource theories

Bits, bears, and beyond in Banff

Ant-Man and the Quantum Realm

Holography and the MERA

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this: