Tag Archives: physics

A classical foreshadow of John Preskill’s Bell Prize

Posted on by
Reply

Editor’s Note: This post was co-authored by Hsin-Yuan Huang (Robert) and Richard Kueng.

John Preskill, Richard P. Feynman Professor of Theoretical Physics at Caltech, has been named the 2024 John Stewart Bell Prize recipient. The prize honors John’s contributions in “the developments at the interface of efficient learning and processing of quantum information in quantum computation, and following upon long standing intellectual leadership in near-term quantum computing.” The committee cited John’s seminal work defining the concept of the NISQ (noisy intermediate-scale quantum) era, our joint work “Predicting Many Properties of a Quantum System from Very Few Measurements” proposing the classical shadow formalism, along with subsequent research that builds on classical shadows to develop new machine learning algorithms for processing information in the quantum world.

We are truly honored that our joint work on classical shadows played a role in John winning this prize. But as the citation implies, this is also a much-deserved “lifetime achievement” award. For the past two and a half decades, first at IQI and now at IQIM, John has cultivated a wonderful, world-class research environment at Caltech that celebrates intellectual freedom, while fostering collaborations between diverse groups of physicists, computer scientists, chemists, and mathematicians. John has said that his job is to shield young researchers from bureaucratic issues, teaching duties and the like, so that we can focus on what we love doing best. This extraordinary generosity of spirit has been responsible for seeding the world with some of the bests minds in the field of quantum information science and technology.

A cartoon depiction of John Preskill (Middle), Hsin-Yuan Huang (Left), and Richard Kueng (Right). [Credit: Chi-Yun Cheng]

It is in this environment that the two of us (Robert and Richard) met and first developed the rudimentary form of classical shadows — inspired by Scott Aaronson’s idea of shadow tomography. While the initial form of classical shadows is mathematically appealing and was appreciated by the theorists (it was a short plenary talk at the premier quantum information theory conference), it was deemed too abstract to be of practical use. As a result, when we submitted the initial version of classical shadows for publication, the paper was rejected. John not only recognized the conceptual beauty of our initial idea, but also pointed us towards a direction that blossomed into the classical shadows we know today. Applications range from enabling scientists to more efficiently understand engineered quantum devices, speeding up various near-term quantum algorithms, to teaching machines to learn and predict the behavior of quantum systems.

Congratulations John! Thank you for bringing this community together to do extraordinarily fun research and for guiding us throughout the journey.

Discoveries at the Dibner

Posted on by
Reply

This past summer, our quantum thermodynamics research group had the wonderful opportunity to visit the Dibner Rare Book Library in D.C. Located in a small corner of the Smithsonian National Museum of American History, tucked away behind flashier exhibits, the Dibner is home to thousands of rare books and manuscripts, some dating back many centuries.

Our advisor, Nicole Yunger Halpern, has a special connection to the Dibner, having interned there as an undergrad. She’s remained in contact with the head librarian, Lilla Vekerdy. For our visit, the two of them curated a large spread of scientific work related to thermodynamics, physics, and mathematics. The tomes ranged from a 1500s print of Euclid’s Elements to originals of Einstein’s manuscripts with hand-written notes in the margin.

The print of Euclid’s Elements was one of the standout exhibits. It featured a number of foldout nets of 3D solids, which had been cut and glued into the book by hand. Several hundred copies of this print are believed to have been made, each of them containing painstakingly crafted paper models. At the time, this technique was an innovation, resulting from printers’ explorations of the then-young art of large-scale book publication.

Another interesting exhibit was rough notes on ideal gases written by Planck, one of the fathers of quantum mechanics. Ideal gases are the prototypical model in statistical mechanics, capturing to high accuracy the behaviour of real gases within certain temperatures and pressures. The notes contained comparisons between Boltzmann, Ehrenfest, and Planck’s own calculations for classical and quantum ideal gases. Though the prose was in German, some results were instantly recognizable, such as the plot of the specific heat of a classical ideal gas, showing the stepwise jump as degrees of freedom freeze out. 

Looking through these great physicists’ rough notes, scratched-out ideas, and personal correspondences was a unique experience, helping humanize them and place their work in historical context. Understanding the history of science doesn’t just need to be for historians, it can be useful for scientists themselves! Seeing how scientists persevered through unknowns, grappling with doubts and incomplete knowledge to generate new ideas, is inspiring. But when one only reads the final, polished result in a modern textbook, it can be difficult to appreciate this process of discovery. Another reason to study the historical development of scientific results is that core concepts have a way of arising time and again across science. Recognizing how these ideas have arisen in the past is insightful. Examining the creative processes of great scientists before us helps develop our own intuition and skillset.

Thanks to our advisor for this field trip – and make sure to check out the Dibner next time you’re in DC! 

Identical twins and quantum entanglement

Posted on by
3

“If I had a nickel for every unsolicited and very personal health question I’ve gotten at parties, I’d have paid off my medical school loans by now,” my doctor friend complained. As a physicist, I can somewhat relate. I occasionally find myself nodding along politely to people’s eccentric theories about the universe. A gentleman once explained to me how twin telepathy (the phenomenon where, for example, one twin feels the other’s pain despite being in separate countries) comes from twins’ brains being entangled in the womb. Entanglement is a nonclassical correlation that can exist between spatially separated systems. If two objects are entangled, it’s possible to know everything about both of them together but nothing about either one. Entangling two particles (let alone full brains) over tens of kilometres (let alone full countries) is incredibly challenging. “Using twins to study entanglement, that’ll be the day,” I thought. Well, my last paper did something like that. 

In theory, a twin study consists of two people that are as identical as possible in every way except for one. What that allows you to do is isolate the effect of that one thing on something else. Aleksander Lasek (postdoc at QuICS), David Huse (professor of physics at Princeton), Nicole Yunger Halpern (NIST physicist and Quantum Frontiers blogger), and I were interested in isolating the effects of quantities’ noncommutation (explained below) on entanglement. To do so, we first built a pair of twins and then compared them. 

Consider a well-insulated thermos filled with soup. The heat and the number of “soup particles” inside the thermos are conserved. So the energy and the number of “soup particles” are conserved quantities. In classical physics, conserved quantities commute. This means that we can simultaneously measure the amount of each conserved quantity in our system, like the energy and number of soup particles. However, in quantum mechanics, this needn’t be true. Measuring one property of a quantum system can change another measurement’s outcome.

Conserved quantities’ noncommutation in thermodynamics has led to some interesting results. For example, it’s been shown that conserved quantities’ noncommutation can decrease the rate of entropy production. For the purposes of this post, entropy production is something that limits engine efficiency—how well engines can convert fuel to useful work. For example, if your car engine had zero entropy production (which is impossible), it would convert 100% of the energy in your car’s fuel into work that moved your car along the road. Current car engines can convert about 30% of this energy, so it’s no wonder that people are excited about the prospective application of decreasing entropy production. Other results (like this one and that one) have connected noncommutation to potentially hindering thermalization—the phenomenon where systems interact until they have similar properties, like when a cup of coffee cools. Thermalization limits memory storage and battery lifetimes. Thus, learning how to resist thermalization could also potentially lead to better technologies, such as longer-lasting batteries. 

One can measure the amount of entanglement within a system, and as quantum particles thermalize, they entangle. Given the above results about thermalization, we might expect that noncommutation would decrease entanglement. Testing this expectation is where the twins come in.

Say we built a pair of twins that were identical in every way except for one. Nancy, the noncommuting twin, has some features that don’t commute, say, her hair colour and height. This means that if we measure her height, we’ll have no idea what her hair colour is. For Connor, the commuting twin, his hair colour and height commute, so we can determine them both simultaneously. Which twin has more entanglement? It turns out it’s Nancy.

Disclaimer: This paragraph is written for an expert audience. Our actual models consist of 1D chains of pairs of qubits. Each model has three conserved quantities (“charges”), which are sums over local charges on the sites. In the noncommuting model, the three local charges are tensor products of Pauli matrices with the identity (XI, YI, ZI). In the commuting model, the three local charges are tensor products of the Pauli matrices with themselves (XX, YY, ZZ). The paper explains in what sense these models are similar. We compared these models numerically and analytically in different settings suggested by conventional and quantum thermodynamics. In every comparison, the noncommuting model had more entanglement on average.

Our result thus suggests that noncommutation increases entanglement. So does charges’ noncommutation promote or hinder thermalization? Frankly, I’m not sure. But I’d bet the answer won’t be in the next eccentric theory I hear at a party.

Building a Koi pond with Lie algebras

Posted on by
3

When I was growing up, one of my favourite places was the shabby all-you-can-eat buffet near our house. We’d walk in, my mom would approach the hostess to explain that, despite my being abnormally large for my age, I qualified for kids-eat-free, and I would peel away to stare at the Koi pond. The display of different fish rolling over one another was bewitching. Ten-year-old me would have been giddy to build my own Koi pond, and now I finally have. However, I built one using Lie algebras.

The different fish swimming in the Koi pond are, in many ways, like charges being exchanged between subsystems. A “charge” is any globally conserved quantity. Examples of charges include energy, particles, electric charge, or angular momentum. Consider a system consisting of a cup of coffee in your office. The coffee will dynamically exchange charges with your office in the form of heat energy. Still, the total energy of the coffee and office is conserved (assuming your office walls are really well insulated). In this example, we had one type of charge (heat energy) and two subsystems (coffee and office). Consider now a closed system consisting of many subsystems and many different types of charges. The closed system is like the finite Koi pond with different charges like the different fish species. The charges can move around locally, but the total number of charges is globally fixed, like how the fish swim around but can’t escape the pond. Also, the presence of one type of charge can alter another’s movement, just as a big fish might block a little one’s path. 

Unfortunately, the Koi pond analogy reaches its limit when we move to quantum charges. Classically, charges commute. This means that we can simultaneously determine the amount of each charge in our system at each given moment. In quantum mechanics, this isn’t necessarily true. In other words, classically, I can count the number of glossy fish and matt fish. But, in quantum mechanics, I can’t.

So why does this matter? Subsystems exchanging charges are prevalent in thermodynamics. Quantum thermodynamics extends thermodynamics to include small systems and quantum effects. Noncommutation underlies many important quantum phenomena. Hence, studying the exchange of noncommuting charges is pivotal in understanding quantum thermodynamics. Consequently, noncommuting charges have emerged as a rapidly growing subfield of quantum thermodynamics. Many interesting results have been discovered from no longer assuming that charges commute (such as these). Until recently, most of these discoveries have been theoretical. Bridging these discoveries to experimental reality requires Hamiltonians (functions that tell you how your system evolves in time) that move charges locally but conserve them globally. Last year it was unknown whether these Hamiltonians exist, what they look like generally, how to build them, and for what charges you could find them.

Nicole Yunger Halpern (NIST physicist, my co-advisor, and Quantum Frontiers blogger) and I developed a prescription for building Koi ponds for noncommuting charges. Our prescription allows you to systematically build Hamiltonians that overtly move noncommuting charges between subsystems while conserving the charges globally. These Hamiltonians are built using Lie algebras, abstract mathematical tools that can describe many physical quantities (including everything in the standard model of particle physics and space-time metric). Our results were recently published in npj QI. We hope that our prescription will bolster the efforts to bridge the results of noncommuting charges to experimental reality.

In the end, a little group theory was all I needed for my Koi pond. Maybe I’ll build a treehouse next with calculus or a remote control car with combinatorics.

Balancing the tradeoff

Posted on by
1

So much to do, so little time. Tending to one task is inevitably at the cost of another, so how does one decide how to spend their time? In the first few years of my PhD, I balanced problem sets, literature reviews, and group meetings, but at the detriment to my hobbies. I have played drums my entire life, but I largely fell out of practice in graduate school. Recently, I made time to play with a group of musicians, even landing a couple gigs in downtown Austin, Texas, “live music capital of the world.” I have found attending to my non-physics interests makes my research hours more productive and less taxing. Finding the right balance of on- versus off-time has been key to my success as my PhD enters its final year.

Of course, life within physics is also full of tradeoffs. My day job is as an experimentalist. I use tightly focused laser beams, known as optical tweezers, to levitate micrometer-sized glass spheres. I monitor a single microsphere’s motion as it undergoes collisions with air molecules, and I study the system as an environmental sensor of temperature, fluid flow, and acoustic waves; however, by night I am a computational physicist. I code simulations of interacting qubits subject to kinetic constraints, so-called quantum cellular automata (QCA). My QCA work started a few years ago for my Master’s degree, but my interest in the subject persists. I recently co-authored one paper summarizing the work so far and another detailing an experimental implementation.

The author doing his part to “keep Austin weird” by playing the drums dressed as grackle (note the beak), the central-Texas bird notorious for overrunning grocery store parking lots.
Balancing research interests: Trapping a glass microsphere with optical tweezers.
Balancing research interests: Visualizing the time evolution of four different QCA rules.

QCA, the subject of this post, are themselves tradeoff-aware systems. To see what I mean, first consider their classical counterparts cellular automata. In their simplest construction, the system is a one-dimensional string of bits. Each bit takes a value of 0 or 1 (white or black). The bitstring changes in discrete time steps based on a simultaneously-applied local update rule: Each bit, along with its two nearest-neighbors, determine the next state of the central bit. Put another way, a bit either flips, i.e., changes 0 to 1 or 1 to 0, or remains unchanged over a timestep depending on the state of that bit’s local neighborhood. Thus, by choosing a particular rule, one encodes a trade off between activity (bit flips) and inactivity (bit remains unchanged). Despite their simple construction, cellular automata dynamics are diverse; they can produce fractals and encryption-quality random numbers. One rule even has the ability to run arbitrary computer algorithms, a property known as universal computation.

Classical cellular automata. Left: rule 90 producing the fractal Sierpiński’s triangle. Middle: rule 30 can be used to generate random numbers. Right: rule 110 is capable of universal computation.

In QCA, bits are promoted to qubits. Instead of being just 0 or 1 like a bit, a qubit can be a continuous mixture of both 0 and 1, a property called superposition. In QCA, a qubit’s two neighbors being 0 or 1 determine whether or not it changes. For example, when in an active neighborhood configuration, a qubit can be coded to change from 0 to “0 plus 1” or from 1 to “0 minus 1”. This is already a head-scratcher, but things get even weirder. If a qubit’s neighbors are in a superposition, then the center qubit can become entangled with those neighbors. Entanglement correlates qubits in a way that is not possible with classical bits.

Do QCA support the emergent complexity observed in their classical cousins? What are the effects of a continuous state space, superposition, and entanglement? My colleagues and I attacked these questions by re-examining many-body physics tools through the lens of complexity science. Singing the lead, we have a workhorse of quantum and solid-state physics: two-point correlations. Singing harmony we have the bread-and-butter of network analysis: complex-network measures. The duet between the two tells the story of structured correlations in QCA dynamics.

In a bit more detail, at each QCA timestep we calculate the mutual information between all qubits i and all other qubits j. Doing so reveals how much there is to learn about one qubit by measuring another, including effects of quantum entanglement. Visualizing each qubit as a node, the mutual information can be depicted as weighted links between nodes: the more correlated two qubits are, the more strongly they are linked. The collection of nodes and links makes a network. Some QCA form unstructured, randomly-linked networks while others are highly structured. 

Complex-network measures are designed to highlight certain structural patterns within a network. Historically, these measures have been used to study diverse networked-systems like friend groups on Facebook, biomolecule pathways in metabolism, and functional-connectivity in the brain. Remarkably, the most structured QCA networks we observed quantitatively resemble those of the complex systems just mentioned despite their simple construction and quantum unitary dynamics. 

Visualizing mutual information networks. Left: A Goldilocks-QCA generated network. Right: a random network.

What’s more, the particular QCA that generate the most complex networks are those that balance the activity-inactivity trade-off. From this observation, we formulate what we call the Goldilocks principle: QCA that generate the most complexity are those that change a qubit if and only if the qubit’s neighbors contain an equal number of 1’s and 0’s. The Goldilocks rules are neither too inactive nor too active, balancing the tradeoff to be “just right.”  We demonstrated the Goldilocks principle for QCA with nearest-neighbor constraints as well as QCA with nearest-and-next-nearest-neighbor constraints.

To my delight, the scientific conclusions of my QCA research resonate with broader lessons-learned from my time as a PhD student: Life is full of trade-offs, and finding the right balance is key to achieving that “just right” feeling.

Machine learning the arXiv

Posted on by
12

Over the last year or so, the machine learning wave has really been sweeping through the field of condensed matter physics. Machine learning techniques have been applied to condensed matter physics before, but very sparsely and with little recognition. These days, I guess (partially) due to the general machine learning and AI hype, the amount of such studies skyrocketed (I admit to contributing to that..). I’ve been keeping track of this using the arXiv and Twitter (@Evert_v_N), but you should know about this website for getting an overview of the physics & machine learning papers: https://physicsml.github.io/pages/papers.html.

This effort of applying machine learning to physics is a serious attempt at trying to understand how such tools could be useful in a variety of ways. It isn’t very hard to get a neural network to learn ‘something’ from physics data, but it is really hard to find out what – and especially how – the network does that. That’s why toy cases such as the Ising model or the Kosterlitz-Thouless transition have been so important!

When you’re keeping track of machine learning and AI developments, you soon realize that there are examples out there of amazing feats. Being able to generate photo-realistic pictures given just a sentence. e.g. “a brown bird with golden speckles and red wings is sitting on a yellow flower with pointy petals”, is (I think..) pretty cool. I can’t help but wonder if we’ll get to a point where we can ask it to generate “the groundstate of the Heisenberg model on a Kagome lattice of 100×100”…

Another feat I want to mention, and the main motivation for this post, is that of being able to encode words as vectors. That doesn’t immediately seem like a big achievement, but it is once you want to have ‘similar’ words have ‘similar’ vectors. That is, you intuitively understand that Queen and King are very similar, but differ basically only in gender. Can we teach that to a computer (read: neural network) by just having it read some text? Turns out we can. The general encoding of words to vectors is aptly named ‘Word2Vec’, and some of the top algorithms that do that were introduced here (https://arxiv.org/abs/1301.3781) and here (https://arxiv.org/abs/1310.4546). The neat thing is that we can actually do arithmetics with these words encoded as vectors, so that the network learns (with no other input than text!):

  • King – Man + Woman = Queen
  • Paris – France + Italy = Rome

In that spirit, I wondered if we can achieve the same thing with physics jargon. Everyone knows, namely, that “electrons + two dimensions + magnetic field = Landau levels”. But is that clear from condensed matter titles?

Try it yourself

If you decide at this point that the rest of the blog is too long, at least have a look here: everthemore.pythonanywhere.com or skip to the last section. That website demonstrates the main point of this post. If that sparks your curiosity, read on!

This post is mainly for entertainment, and so a small disclaimer is in order: in all of the results below, I am sure things can be improved upon. Consider this a ‘proof of principle’. However, I would be thrilled to see what kind of trained models you can come up with yourself! So for that purpose, all of the code (plus some bonus content!) can be found on this github repository: https://github.com/everthemore/physics2vec.

Harvesting the arXiv

The perfect dataset for our endeavor can be found in the form of the arXiv. I’ve written a small script (see github repository) that harvests the titles of a given section from the arXiv. It also has options for getting the abstracts, but I’ll leave that for a separate investigation. Note that in principle we could also get the source-files of all of these papers, but doing that in bulk requires a payment; and getting them one by one will 1) take forever and 2) probably get us banned.

Collecting all this data of the physics:cond-mat subsection took right about 1.5 hours and resulted in 240737 titles and abstracts (I last ran this script on November 20th, 2017). I’ve filtered them by year and month, and you can see the result in Fig.1 below. Seems like we have some catching up to do in 2017 still (although as the inset shows, we have nothing to fear. November is almost over, but we still have the ‘getting things done before x-mas’ rush coming up!).

numpapers

Figure 1: The number of papers in the cond-mat arXiv section over the years. We’re behind, but the year isn’t over yet! (Data up to Nov 20th 2017)

Analyzing n-grams

After tidying up the titles (removing LaTeX, converting everything to lowercase, etc.), the next thing to do is to train a language model on finding n-grams. N-grams are basically fixed n-word expressions such as ‘cooper pair’ (bigram) or ‘metal insulator transition’ (trigram). This makes it easier to train a Word2Vec encoding, since these phrases are fixed and can be considered a single word. The python module we’ll use for Word2Vec is gensim (https://radimrehurek.com/gensim/), and it conveniently has phrase-detection built-in. The language model it builds reports back to us the n-grams it finds, and assigns them a score indicating how certain it is about them. Notice that this is not the same as how frequently it appears in the dataset. Hence an n-gram can appear fewer times than another, but have a higher certainty because it always appears in the same combination. For example, ‘de-haas-van-alphen’ appears less than, but is more certain than, ‘cooper-pair’, because ‘pair’ does not always come paired (pun intended) with ‘cooper’. I’ve analyzed up to 4-grams in the analysis below.

I can tell you’re curious by now to find out what some of the most certain n-grams in cond-mat are (again, these are not necessarily the most frequent), so here are some interesting findings:

  • The most certain n-grams are all surname combo’s, Affleck-Kennedy-Lieb-Tasaki being the number 1. Kugel-Khomskii is the most certain 2-name combo and Einstein-Podolksi-Rosen the most certain 3-name combo.
  • The first certain non-name n-gram is a ‘quartz tuning fork’, followed by a ‘superconducting coplanar waveguide resonator’. Who knew.
  • The bigram ‘phys. rev.’ and trigram ‘phys. rev. lett.’ are relatively high up in the confidence lists. These seem to come from the “Comment on […]”-titles on the arXiv.
  • I learned that there is such a thing as a Lefschetz thimble. I also learned that those things are called thimbles in English (we (in Holland) call them ‘finger-hats’!).

In terms of frequency however, which is probably more of interest to us, the most dominant n-grams are Two-dimensional, Quantum dot, Phase transition, Magnetic field, One dimensional and Bose-Einstein (in descending order). It seems 2D is still more popular than 1D, and all in all the top n-grams do a good job at ‘defining’ condensed matter physics. I’ll refer you to the github repository code if you want to see a full list! You’ll find there a piece of code that produces wordclouds from the dominant words and n-grams too, such as this one:

caltechwordcloud.png

For fun though, before we finally get to the Word2Vec encoding, I’ve also kept track of all of these as a function of year, so that we can now turn to finding out which bigrams have been gaining the most popularity. The table below shows the top 5 n-grams for the period 2010 – 2016 (not including 2017) and for the period 2015 – Nov 20th 2017.

2010-2016

2015 – November 20th 2017
Spin liquids  Topological phases & transitions
 Weyl semimetals  Spin chains
 Topological phases & transitions  Machine learning
 Surface states  Transition metal dichalcogenides
 Transition metal dichalcogenides  Thermal transport
 Many-body localization  Open quantum systems

Actually, the real number 5 in the left column was ‘Topological insulators’, but given number 3 I skipped it. Also, this top 5 includes a number 6 (!), which I just could not leave off given that everyone seems to have been working on MBL. If we really want to be early adopters though, taking only the last 1.8 years (2015 – now, Nov 20th 2017)  in the right column of the table shows some interesting newcomers. Surprisingly, many-body localization is not even in the top 20 anymore. Suffice it to say, if you have been working on anything topology-related, you have nothing to worry about. Machine learning is indeed gaining lots of attention, but we’ve yet to see if it doesn’t go the MBL-route (I certainly don’t hope so!). Quantum computing does not seem to be on the cond-mat radar, but I’m certain we would find that high up in the quant-ph arXiv section.

CondMat2Vec

Alright, finally time to use some actual neural networks for machine learning. As I started this post, what we’re about to do is try to train a network to encode/decode words into vectors, while simultaneously making sure that similar words (by meaning!) have similar vectors. Now that we have the n-grams, we want the Word2Vec algorithm to treat these as words by themselves (they are, after all, fixed combinations).

In the Word2Vec algorithm, we get to decide the length of the vectors that encode words ourselves. Larger vectors means more freedom in encoding words, but also makes it harder to learn similarity. In addition, we get to choose a window-size, indicating how many words the algorithm will look ahead to analyze relations between words. Both of these parameters are free for you to play with if you have a look at the source code repository. For the website everthemore.pythonanywhere.com, I’ve uploaded a size 100 with window-size 10 model, which I found to produce sensible results. Sensible here means “based on my expectations”, such as the previous example of “2D + electrons + magnetic field = Landau levels”. Let’s ask our network some questions.

First, as a simple check, let’s see what our encoding thinks some jargon is similar to:

  • Superconductor ~ Superconducting, Cuprate superconductor, Superconductivity, Layered superconductor, Unconventional superconductor, Superconducting gap, Cuprate, Weyl semimetal, …
  • Majorana ~ Majorana fermion, Majorana mode, Non-abelian, Zero-energy, braiding, topologically protected, …

It seems we could start to cluster words based on this. But the real test comes now, in the form of arithmetics. According to our network (I am listing the top two choices in some cases; the encoder outputs a list of similar vectors, ordered by similarity):

  • Majorana + Braiding = Non-Abelian
  • Electron + Hole = Exciton, Carrier
  • Spin + Magnetic field = Magnetization, Antiferromagnetic
  • Particle + Charge = Electron, Charged particle

And, sure enough:

  • 2D + electrons + magnetic field = Landau level, Magnetoresistance oscillation

The above is just a small sample of the things I’ve tried. See the link in the try it yourself section above if you want to have a go. Not all of the examples work nicely. For example, neither lattice + wave nor lattice + excitation nor lattice + force seem to result in anything related to the word ‘phonon’. I would guess that increasing the window size will help remedy this problem. Even better probably would be to include abstracts!

Outlook

I could play with this for hours, and I’m sure that by including the abstracts and tweaking the vector size (plus some more parameters I haven’t even mentioned) one could optimize this more. Once we have an optimized model, we could start to cluster the vectors to define research fields, visualizing the relations between n-grams (both suggestions thanks to Thomas Vidick and John Preskill!), and many other things. This post has become rather long already however, and I will leave further investigation to a possible future post. I’d be very happy to incorporate anything cool you find yourselves though, so please let me know!

The world of hackers and secrets

Posted on by
16

I’m Evgeny Mozgunov, and some of you may remember my earlier posts on Quantum Frontiers. I’ve recently graduated with a PhD after 6 years in the quantum information group at Caltech. As I’m navigating the job market in quantum physics, it was only a matter of time before I got dragged into a race between startups. Those who can promise impressive quantum speedups for practical tasks get a lot of money from venture capitalists. Maybe there’s something about my mind and getting paid: when I’m paid to do something, I suddenly start coming up with solutions that never occurred to me while I was wandering around as a student. And this time, I’ve noticed a possibility of impressing the public with quantum speedups that nobody has ever used before.

Three former members of John Preskill’s group, Gorjan Alagic, Stacey Jeffery and Stephen Jordan, have already proposed this idea (Circuit Obfuscation Using Braids, p.10), but none of the startups seems to have picked it up. You only need a small quantum computer. Imagine you are in the audience. I ask you to come up with a number. Don’t tell it out loud: instead, write it on a secret piece of paper, and take a little time to do a few mathematical operations based on the number. Then announce the result of those operations. Once you are done, people will automatically be split into two categories. Those with access to a small quantum computer (like the one at IBM) will be able to put on a magic hat (the computer…) and recover your number. But the rest of the audience will be left in awe, with no clue as to how this is even possible. There’s nothing they could do to guess your number based only on the result you announced, unless you’re willing to wait for a few days and they have access to the world’s supercomputing powers.

So far I’ve described the general setting of encryption – a cipher is announced, the key to the cipher is destroyed, and only those who can break the code can decipher.  For instance, if RSA encryption is used for the magic show above, indeed only people with a big quantum computer will be able to recover the secret number. To complete my story, I need to describe what the result that you announce (the cipher) looks like:

A sequence of instructions for a small quantum computer that is equivalent to a simple instruction for spitting out your number. However, the announced sequence of instructions is obfuscated, such that you can’t just read off the number from it.

You really need to feed the sequence into a quantum computer, and see what it outputs. Obfuscation is more general than encryption, but here we’re going to use it as a method of encryption.

Alagic et al. taught us how to do something called obfuscation by compiling for a quantum computer: much like when you compile a .c file in your CS class, you can’t really understand the .out file. Of course you can just execute the .out file, but not if it describes a quantum circuit, unless you have access to a quantum computer. The proposed classical compiler turns either a classical or a quantum algorithm into a hard-to-read quantum circuit that looks like braidsBraid_1000.gif. Unfortunately, any obfuscation by compiling scheme has the problem that whoever understands the compiler well enough will be able to actually read the .out file (or notice a pattern in braids reduced to a compact “normal” form), and guess your number without resorting to a quantum computer. Surprisingly, even though Alagic et al.’s scheme doesn’t claim any protection under this attack, it still satisfies one of the theoretical definitions of obfuscation: if two people write two different sets of instructions to perform the same operation, and then each obfuscate their own set of instructions by a restricted set of tricks, then it should be impossible to tell from the end result which program was obtained by whom.

forQF2.jpg

Theoretical obfuscation can be illustrated by these video game Nier cosplayers: when they put on their wig and blindfold, they look like the same person. The character named 2B is an android, whose body is disposable, and whose mind is a set of instructions stored on a server. Other characters try to hack her mind as the story progresses.

Quantum scientists can have their own little world of hackers and secrets, organized in the following way: some researchers present their obfuscated code outputting a secret message, and other researchers become hackers trying to break it. Thanks to another result by Alagic et al, we know that hard-to-break obfuscated circuits secure against classical computers exist. But we don’t know how the obfuscator that produces those worst-case instances reliably looks like, so a bit of crowdsourcing to find it is in order. It’s a free-for-all, where all tools and tricks are allowed. In fact, even you can enter! All you need to know is a universal gate set H,T = R(π/4),CNOT and good old matrix multiplication. Come up with a product of these matrices that multiplies to a bunch of X‘s (X=HT⁴H), but such that only you know on which qubits the X are applied. This code will spit out your secret bitstring on an input of all 0’es. Publish it and wait until some hacker breaks it!

Here’s mine, can anyone see what’s my secret bitstring?

Obfuscated circuit.png

One can run it on a 5 qubit quantum computer in less than 1ms. But if you try to multiply the corresponding 32×32 matrices on your laptop, it takes more than 1ms. Quantum speedup right there. Of course I didn’t prove that there’s no better way of finding out my secret than multiplying matrices. In fact, had I used only even powers of the matrix T in the picture above, then there is a classical algorithm available in open source (Aaronson, Gottesman) that recovers the number without having to multiply large matrices.

I’m in luck: startups and venture capitalists never cared about theoretical proofs, it only has to work until it fails. I think they should give millions to me instead of D-wave. Seriously, there’s plenty of applications for practical obfuscation, besides magic shows. One can set up a social network where posts are gibberish except for those who have a quantum computer (that would be a good conspiracy theory some years from now). One can verify when a private company claims to sell a small quantum computer.

I’d like to end on a more general note: small quantum computers are already faster than classical hardware at multiplying certain kinds of matrices. This has already been proven for a restricted class of quantum computers and a task called boson sampling. If there’s a competition in matrix multiplication somewhere in the world, we can already win.

The entangled fabric of space

Posted on by
4

We live in the information revolution. We translate everything into vast sequences of ones and zeroes. From our personal email to our work documents, from our heart rates to our credit rates, from our preferred movies to our movie preferences, all things information are represented using this minimal {0,1} alphabet which our digital helpers “understand” and process. Many of us physicists are now taking this information revolution at heart and embracing the “It from qubit” motto. Our dream: to understand space, time and gravity as emergent features in a world made of information – quantum information.

Over the past two years, I have been obsessively trying to understand this profound perspective more rigorously. Recently, John Preskill and I have taken a further step in this direction in the recent paper: quantum code properties from holographic geometries. In it, we make progress in interpreting features of the holographic approach to quantum gravity in the terms of quantum information constructs. 

In this post I would like to present some context for this work through analogies which hopefully help intuitively convey the general ideas. While still containing some technical content, this post is not likely to satisfy those readers seeking a precise in-depth presentation. To you I can only recommend the masterfully delivered lecture notes on gravity and entanglement by Mark Van Raamsdonk.  

Entanglement as a cat’s cradle

Cats-cradle

A cat’s cradle serves as a crude metaphor for quantum mechanical entanglement. The full image provides a complete description of the string and how it is laced in a stable configuration around the two hands. However, this lacing does not describe a stable configuration of half the string on one hand. The string would become disentangled and fall if we were to suddenly remove one of the hands or cut through the middle.

Of all the concepts needed to explain emergent spacetime, maybe the most difficult is that of quantum entanglement. While the word seems to convey some kind of string wound up in a complicated way, it is actually a quality which may describe information in quantum mechanical systems. In particular, it applies to a system for which we have a complete description as a whole, but are only capable of describing certain statistical properties of its parts. In other words, our knowledge of the whole loses predictive power when we are only concerned with the parts. Entanglement entropy is a measure of information which quantifies this.

While our metaphor for entanglement is quite crude, it will serve the purpose of this post. Namely, to illustrate one of the driving premises for the holographic approach to quantum gravity, that the very structure of spacetime is emergent and built up from entanglement entropy.

Knit and crochet your way into the manifolds

But let us bring back our metaphors and try to convey the content of this identification. For this, we resort to the unlikely worlds of knitting and crochet. Indeed, by a planned combination of individual loops and stitches, these traditional crafts are capable of approximating any kind of surface (2D Riemannian surface would be the technical term).

Flat knit (K =0)
Positive curvature crochet (K >0)
Negative curvature crochet (K <0)

Here I have presented some examples with uniform curvature R: flat in green, positive curvature (ball) in yellow and negative curvature (coral reef) in purple. While actual practitioners may be more interested in getting the shape right on hats and socks for loved ones, for us the point is that if we take a step back, these objects built of simple loops, hooks and stitches could end up looking a lot like the smooth surfaces that a physicist might like to use to describe 2D space. This is cute, but can we push this metaphor even further?

Well, first of all, although the pictures above are only representing 2D surfaces, we can expect that a similar approach should allow approximating 3D and even higher dimensional objects (again the technical term is Riemannian manifolds). It would just make things much harder to present in a picture. These woolen structures are, in fact, quite reminiscent of tensor networks, a modern mathematical construct widely used in the field of quantum information. There too, we combine basic building blocks (tensors) through simple operations (tensor index contraction) to build a more complex composite object. In the tensor network world, the structure of the network (how its nodes are connected to other nodes) generically defines the entanglement structure of the resulting object.

PentagonTensorNetwork

This regular tensor network layout was used to describe hyperbolic space which is similar to the purple crochet. However, they apriori look quite dissimilar due to the use of the Poincaré disk model where tensors further from the center look smaller. Another difference is that the high degree of regularity is achieved at the expense of having very few tensors per curvature radius (as compared to its purple crochet cousin). However, planarity and regularity don’t seem to be essential so the crochet probably provides a better intuitive picture.

Roughly speaking, tensor networks are ingenious ways of encoding (quantum) inputs into (quantum) outputs. In particular, if you enter some input at the boundary of your tensor network, the tensors do the work of processing that information throughout the network so that if you ask for an output at any one of the nodes in the bulk of the tensor network, you get the right encoded answer. In other words, the information we input into the tensor network begins its journey at the dangling edges found at the boundary of the network and travels through the bulk edges by exploiting them as information bridges between the nodes of the network.

In the figure representing the cat’s cradle, these dangling input edges can be though of as the fingers holding the wool. Now, if we partition these edges into two disjoint sets (say, the fingers on the left hand and the fingers on the right hand, respectively), there will be some amount of entanglement between them. How much? In general, we cannot say, but under certain assumptions we find that it is proportional to the minimum cut through the network. Imagine you had an incredible number of fingers holding your wool structure. Now separate these fingers arbitrarily into two subsets L and R (we may call them left hand and right hand, although there is nothing right or left handy about them). By pulling left hand and right hand apart, the wool might stretch until at some point it breaks. How many threads will break? Well, the question is analogous to the entanglement one. We might expect, however, that a minimal number of threads break such that each hand can go its own way. This is what we call the minimal cut. In tensor networks, entanglement entropy is always bounded above by such a minimal cut and it has been confirmed that under certain conditions entanglement also reaches, or approximates, this bound. In this respect, our wool analogy seems to be working out.

Holography

Holography, in the context of black holes, was sparked by a profound observation of Jacob Bekenstein and Stephen Hawking, which identified the surface area of a black hole horizon (in Planck units) with its entropy, or information content:BHentropyF1

S_{BH} = \frac{k A_{BH}}{4\ell_p^2} .

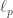Here, S_{BH} is the entropy associated to the black hole, A_{BH} is its horizon area, \ell_p is the Planck length and k is Boltzmann’s constant.
Why is this equation such a big deal? Well, there are many reasons, but let me emphasize one. For theoretical physicists, it is common to get rid of physical units by relating them through universal constants. For example, the theory of special relativity allows us to identify units of distance with units of time through the equation d=ct using the speed of light c. General relativity further allows us to identify mass and energy through the famous E=mc^2. 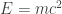By considering the Bekenstein-Hawking entropy, units of area are being swept away altogether! They are being identified with dimensionless units of information (one square meter is roughly 1.4\times10^{69} bits according to the Bousso bound).

Initially, the identification of area and information was proposed to reconcile black holes with the laws of thermodynamics. However, this has turned out to be the main hint leading to the holographic principle, wherein states that describe a certain volume of space in a theory of quantum gravity can also be thought of as being represented at the lower dimensional boundary of the given volume. This idea, put forth by Gerard ‘t Hooft, was later given a more precise interpretation by Leonard Susskind and subsequently by Juan Maldacena through the celebrated AdS/CFT correspondence. I will not dwell in the details of the AdS/CFT correspondence as I am not an expert myself. However, this correspondence gave S. Ryu and T. Takayanagi  (RT) a setting to vastly generalize the identification of area as an information quantity. They proposed identifying the area of minimal surfaces on the bulk (remember the minimal cut?) with entanglement entropy in the boundary theory.

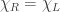Roughly speaking, if we were to split the boundary into two regions, left L and right R it should be possible to also partition the bulk in a way that each piece of the bulk has either L or R in its boundary. Ryu and Takayanagi proposed that the area of the smallest surface \chi_R=\chi_L which splits the bulk in this way would be proportional to the entanglement entropy between the two parts

S_L = S_R = \frac{|\chi_L|}{4G} =\frac{|\chi_R|}{4G}.

It turns out that some quantum field theory states admit such a geometric interpretation. Many high energy theory colleagues have ideas about when this is possible and what are the necessary conditions. By far the best studied setting for this holographic duality is AdS/CFT, where Ryu and Takayanagi first checked their proposal. Here, the entanglement features of  the lowest energy state of a conformal field theory are matched to surfaces in a hyperbolic space (like the purple crochet and the tensor network presented). However, other geometries have been shown to match the RT prediction with respect to the entanglement properties of different states. The key point here is that the boundary states do not have any geometry per se. They just manifest different amounts of entanglement when partitioned in different ways.

Emergence

The holographic program suggests that bulk geometry emerges from the entanglement properties of the boundary state. Spacetime materializes from the information structure of the boundary instead of being a fundamental structure as in general relativity. Am I saying that we should strip everything physical, including space in favor of ones and zeros? Well, first of all, it is not just me who is pushing this approach. Secondly, no one is claiming that we should start making all our physical reasoning in terms of ones and zeros.

Let me give an example. We know that the sea is composed mostly of water molecules. The observation of waves that travel, superpose and break can be labeled as an emergent phenomenon. However, to a surfer, a wave is much more real than the water molecules composing it and the fact that it is emergent is of no practical consequence when trying to predict where a wave will break. A proficient physicist, armed with tools from statistical mechanics (there are more than 10^{25} molecules per liter), could probably derive a macroscopic model for waves from the microscopic theory of particles. In the process of learning what the surfer already understood, he would identify elements of the  microscopic theory which become irrelevant for such questions. Such details could be whether the sea has an odd or even number of molecules or the presence of a few fish.

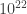In the case of holography, each square meter corresponds to 1.4\times10^{69} bits of entanglement. We don’t even have words to describe anything close to this outrageously large exponent which leaves plenty of room for emergence. Even taking all the information on the internet – estimated at 10^{22} bits (10 zettabits) – we can’t even match the area equivalent of the smallest known particle. The fact that there are so many orders of magnitude makes it difficult to extrapolate our understanding of the geometric domain to the information domain and vice versa. This is precisely the realm where techniques such as those from statistical mechanics successfully get rid of irrelevant details.

High energy theorists and people with a background in general relativity tend to picture things in a continuum language. For example, part of their daily butter are Riemannian or Lorentzian manifolds which are respectively used to describe space and spacetime. In contrast, most of information theory is usually applied to deal with discrete elements such as bits, elementary circuit gates, etc. Nevertheless, I believe it is fruitful to straddle this cultural divide to the benefit of both parties. In a way, the convergence we are seeking is analogous to the one achieved by the kinetic theory of gases, which allowed the unification of thermodynamics with classical mechanics.

So what did we do?

The remarkable success of the geometric RT prediction to different bulk geometries such as the BTZ black holes and the generality of the entanglement result for its random tensor network cousins emboldened us to take the RT prescription beyond its usual domain of application. We considered applying it to arbitrary Riemannian manifolds that are space-like and that can be approximated by a smoothly knit fabric.

Furthermore, we went on to consider the implications that such assumptions would have when the corresponding geometries are interpreted as error-correcting codes. In fact, our work elaborates on the perspective of A. Almheiri, X. Dong and D. Harlow (ADH) where quantum error-correcting code properties of AdS/CFT were laid out; it is hard to overemphasize the influence of this work. Our work considers general geometries and identifies properties a code associated to a specific holographic geometry should satisfy.

In the cat cradle/fabric metaphor for holography, the fingers at the boundary constitute the boundary theory without gravity and the resulted fabric represents a bulk geometry in the corresponding bulk gravitational theory. Bulk observables may be represented in different ways on the boundary, but not arbitrarily. This raises the question of which parts of the bulk correspond to which parts of the boundary. In general, there is not a one to one mapping. However, if we partition the boundary in two parts L and R, we expect to be able to split the bulk into two corresponding regions  {\mathcal E}[L]  and  {\mathcal E}[R]. This is the content of the entanglement wedge hypothesis, which is our other main assumption.  In our metaphor, one could imagine that we pull the left fingers up and the right fingers down (taking care not to get hurt). At some point, the fabric breaks through \chi_R into two pieces. In the setting we are concerned with, these pieces maintain part of the original structure, which tells us which bulk information was available in one piece of the boundary and which part was available in the other.

Although we do not produce new explicit examples of such codes, we worked our way towards developing a language which translates between the holographic/geometric perspective and the coding theory perspective. We specifically build upon the language of operator algebra quantum error correction (OAQEC) which allows individually focusing on different parts of the logical message. In doing so we identified several coding theoretic bounds and quantities, some of which we found to be applicable beyond the context of holography. A particularly noteworthy one is a strengthening of the quantum Singleton bound, which defines a trade-off between how much logical information can be packed in a code, how much physical space is used for encoding this information and how well-protected the information is from erasures.

One of the central observations of ADH highlights how quantum codes have properties from both classical error-correcting codes and secret sharing schemes. On the one hand, logical encoded information should be protected from loss of small parts of the carrier, a property quantified by the code distance. On the other hand, the logical encoded information should not become accessible until a sufficiently large part of the carrier is available to us. This is quantified by the threshold of a corresponding secret sharing scheme. We call this quantity price as it identifies how much of the carrier we would need before someone could reconstruct the message faithfully. In general, it is hard to balance these two competing requirements; a statement which can be made rigorous. This kind of complementarity has long been recognized in quantum cryptography. However, we found that according to holographic predictions, codes admitting a geometric interpretation achieve a remarkable optimality in the trade-off between these features.

Our exploration of alternative geometries is rewarded by the following guidelines

CantorWedge

In uberholography, bulk observables are accessible in a Cantor type fractal shaped subregion of the boundary. This is illustrated on the Poincare disc presentation of negatively curved bulk.

  • Hyperbolic geometries predict a fixed polynomial scaling for code distance. This is illustrated by a feature we call uberholography. We use this name because there is an excess of holography wherein bulk observables can be represented on intricate subsets of the boundary which have fractal dimension even smaller than the boundary itself.
  • Hyperbolic geometries suggest the possibility of decoding procedures which are local on the boundary geometry. This property may be connected to the locality of the corresponding boundary field theory.
  • Flat and positive curvature geometries may lead to codes with better parameters in terms of distance and rates (ratio of logical information to physical information). A hemisphere reaches optimum parameters, saturating coding bounds.

    729px-Cantor_set_in_seven_iterations.svg

    Seven iterations of a ternary Cantor set (dark line) on the unit interval. Each iteration is obtained by punching holes from the previous one and the set obtained in the limit is a fractal.

Current day quantum computers are far from the number of qubits required to invoke an emergent geometry. Nevertheless, it is exhilarating to take a step back and consider how the properties of the codes, and information in general, may be interpreted geometrically. On the other hand, I find that the quantum code language we adapt to the context of holography might eventually serve as a useful tool in distinguishing which boundary features are relevant or irrelevant for the emergent properties of the holographic dual. Ours is but one contribution in a very active field. However, the one thing I am certain about is that these are exciting times to be doing physics.

IQIM Presents …”my father”

Posted on by
2

Debaleena Nandi at Caltech

Debaleena Nandi at Caltech

Following the IQIM teaser, which was made with the intent of creating a wider perspective of the scientist, to highlight the normalcy behind the perception of brilliance and to celebrate the common human struggles to achieve greatness, we decided to do individual vignettes of some of the characters you saw in the video.

We start with Debaleena Nandi, a grad student in Prof Jim Eisenstein’s lab, whose journey from Jadavpur University in West Bengal, India to the graduate school and research facility at the Indian institute of Science, Bangalore, to Caltech has seen many obstacles. We focus on the essentials of an environment needed to manifest the quest for “the truth” as Debaleena says. We start with her days as a child when her double-shift working father sat by her through the days and nights that she pursued her homework.

She highlights what she feels is the only way to growth; working on what is lacking, to develop that missing tool in your skill set, that asset that others might have by birth but you need to inspire by hard work.

Debaleena’s motto: to realize and face your shortcomings is the only way to achievement.

As we build Debaleena up, we also build up the identity of Caltech through its breathtaking architecture that oscillates from Spanish to Goth to modern. Both Debaleena and Caltech are revealed slowly, bit by bit.

This series is about dissecting high achievers, seeing the day to day steps, the bit by bit that adds up to the more often than not, overwhelming, impressive presence of Caltech’s science. We attempt to break it down in smaller vignettes that help us appreciate the amount of discipline, intent and passion that goes into making cutting edge researchers.

Presenting the emotional alongside the rational is something this series aspires to achieve. It honors and celebrates human limitations surrounding limitless boundaries, discoveries and possibilities.

Stay tuned for more vignettes in the IQIM Presents “My _______” Series.

But for now, here is the video. Watch, like and share!

(C) Parveen Shah Production 2014

 

The Navajo connection

Posted on by
Reply

A few months ago, Prof. Keith Schwab brought visiting students and teachers from Navajo Preparatory School to tour some of the IQIM labs, listen to some quick lectures on optics, and talk to scientists. Since this opportunity was only allowed to the one carload that made the 11.5 hour drive from Farmington, NM, everyone involved agreed that we could reach far more students if the IQIM sent Caltech students there. Ana Brown and I both enjoyed speaking with the visiting students and teachers, and responded enthusiastically when Prof. Schwab offered to send us.  My enthusiasm momentarily dimmed when I realized our trip would be occurring in the dead of winter and it was projected to snow while we were there (having only lived in northern and southern California, let’s say I have a heightened sensitivity to weather), but I excitedly spent thanksgiving putting together demonstrations with supplies I found in my closet and garage. I’ve always enjoyed talking about applied math, science, and engineering to anyone, especially anyone young enough to have only heard “math is boring” or “science is too hard” few enough times I can convince them otherwise.  Navajo Prep seemed ideal for this, since the school prepares the students well and sends over 95% of the students to college, and is working to increase student interest in math, science, and engineering.

it's colder than it looks, I swear

Panorama from the center of Navajo Prep

With a suitcase half full of clothes and half full of tools and hacked-together electronics, I was picked up from the airport, and arrived at the school in the afternoon the Monday after Thanksgiving weekend. While Monday was spent arranging which classes I would attend, and what topics I would discuss, my second day involved a trip with the school’s outreach coordinator and Cody, one of the two students who visited Caltech, taking a tour of some of the local highlights, including a traditional Navajo lunch (steam corn stew, roast mutton, and I even tried ach’ii”) and toured the remnants of the cliff dwellings at Mesa Verde, about half an hour from the school. Exploring a region with such a rich history and discussing it with my hosts, who are descendants in part from that history was an incredible experience.

yup, some 70 rooms built in a recess carved into the canyon wall almost a thousand years ago.

Rooms at the Oak Tree House at Mesa Verde

On Wednesday, I began talking to the freshman physics classes about optics, intending to discuss the properties of light, like frequency, speed, wavelength, velocity, energy, and momentum, but to give some context I began with a historical summary of discoveries in optics. I know I was surprised when I was preparing, so you might enjoy answering the same questions that I asked the class. Take a second, and guess when you think the first lenses were made and when wearable glasses were first used. (After you think you have a guess, scroll to the bottom to see how you did.)  When I realized that the class was more interested in seeing rather than hearing about optics, I skimmed over what I’d prepared in order to spend more time on the demonstrations where I showed refraction in glass and explained how that can be derived from assuming a different speed of light in the material. We found lenses for the students to manipulate/play with, and even though historically there were about 300 years between invention of glasses (and the proliferation of lens-making) and the invention of the telescope, some of the students unintentionally built telescopes after taking a second lens from their friends and were shocked to hear that what they had just made was better than the one Galileo used to first discover the four largest moons of Jupiter.

I promise this shot is not advertising for Under Armour.

Measuring focal lengths and observing lensing with a drop of water on a glass slide

We also demonstrated double slit diffraction and calculated light’s wavelength for three different laser pointers to within 5% accuracy using only a tape measure, a post-it, and a knife. I decided not to bring a demonstration to measure the speed of light with a laser, a few mirrors, a computer fan, and a reverse-biased photodiode hooked up to an old speaker, because I couldn’t get the fan to spin fast enough to get a reasonably short delay length. (From that can you guess what my set-up was?) On Thursday, Ana and I gave a similar lecture to a different pair of 90 minute freshman physics classes, and spent the other periods talking with math classes. In calculus, I described the different kinds of math classes offered in college, their applications, and their connections to each other in an attempt to give more meaning to the course titles they would no doubt be reading next fall. In geometry and trigonometry I answered the perennial high school math question: “when will we ever use this?” by talking about some applications in geometric optics.

Since I figure you readers like thinking about this sort of thing, I’ll elaborate: I started with the fact that a light beam’s incident angle (measured from the perpendicular of a surface) is equal to its reflected angle. This means that light propagation, like much of (but not all of) physics, is reversible in all but a few specific cases. As a result, light generated at or passing through the center of a circle is reflected off the circle back to the center. An ellipse has a similar property where light through one focus is all reflected to the other. Try deriving that from the fact that an ellipse is defined to be the set of all points where the sum of the distances to the two foci equals some fixed constant. In the lecture, I then used the fact that a parabola is the set of all points equidistant from a point (the focus) and a line (the directrix) to show that light from the focus is reflected off the parabola and collimated (focused at infinity).

Ana brought some IQIM hats and shirts, which the freshman physics classes seemed to definitely enjoy when we met with each class for 40 minutes on Friday.

We probably tripled the number of high school varsity football players who've worn IQIM gear in that one picture

One of the four freshman physics classes we got to spend time with

I tried to give them an impression of what we do in the IQIM, but I had a hard time giving a satisfactory explanation of the significance of quantum information, and Ana easily convinced me that it would be more engaging to use the 90 minute introduction I had already given them on optics to explain and describe solar energy, since many buildings deep in the Navajo reservation are off the power grid.  There are also plans to construct a large solar power plant on the reservation that will be much cleaner than the three local coal power plants in the region.

I think I made a joke and Ana might have been the only one to laugh. Still, it's proof I can be funny.

Action shot during the lecture on solar

Ana and I also spoke to the senior seminar, which contained the entire graduating class, where she talked about the difficulties transitioning to college experienced by some of her friends in college who were from the Navajo reservation. She gave such great advice on applying to schools, applying for fellowships, and developing a healthy work/life balance, that the only thing I felt like I could contribute was some advice on picking a major (since I’ve picked about 4 different majors), where I described the difference between science and engineering, and talked about different fields within each. I loved how truly helpful I felt when so many of the students told us that they either found certain pieces of advice to be useful, thanked us for introducing them to an idea they hadn’t heard of, or asked us to come back soon.

Occasionally a student asked what I personally do, and their curiosity was rewarded with an explanation that lasted as long as they were interested.  The shortest lasted two sentences and the longest explanation (given to a calculus class of 5 people) involved 30 minutes with my laptop out showing all the steps I take to fabricate nanoscale devices to trap light in almost a cubic-wavelength volume in proximity to an “optically interesting” rare earth ion which my advisor and I hope will provide a viable quantum optical memory.  (Here‘s a little more about our work.)

In the evenings we cheered for the school’s basketball team, had dinner with some of the students and teachers, and discussed the school’s science curriculum and science fair projects. Ana and I consulted on a solar water heating project some of the students were working on, and, after the students all went home for the weekend, I even spent 2 hours in 17ºF weather the last night calibrating an 8″ diameter Schmidt-Cassegrain telescope that had been donated to the school. Compared to Pasadena the viewing was spectacular, and I could easily spot galaxies, nebulae, and discern stripes on Jupiter and the four Galilean moons. I can only expect that some of the students I met will be as excited as I was.

From wikipedia: “The earliest known lenses were made from polished crystal, often quartz, and have been dated as early as 700 BC for Assyrian lenses” and “Around 1284 in Italy, Salvino D’Armate is credited with inventing the first wearable eye glasses.” For anyone who’s interested in the history of science, I’d suggest you check it out.